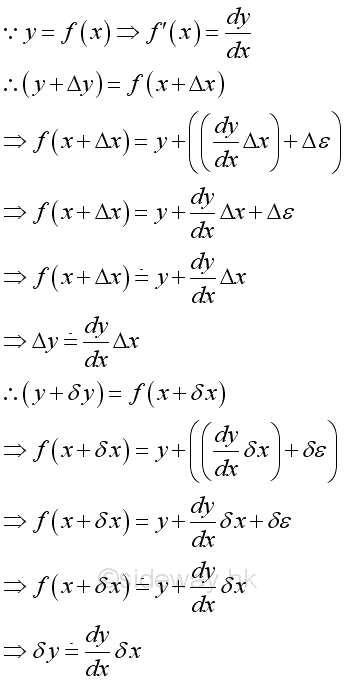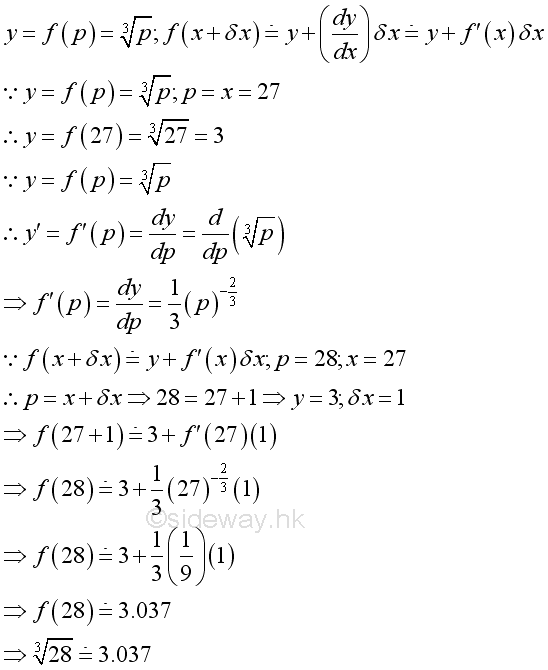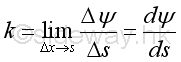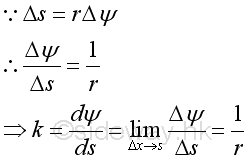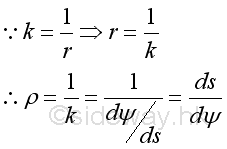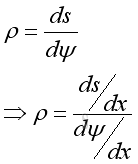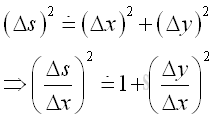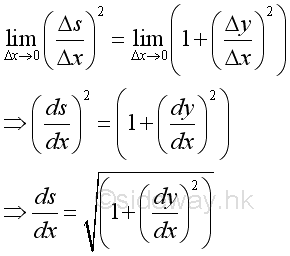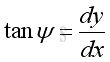Sideway
BICK BLOG from Sideway
Sideway
BICK BLOG from Sideway
|
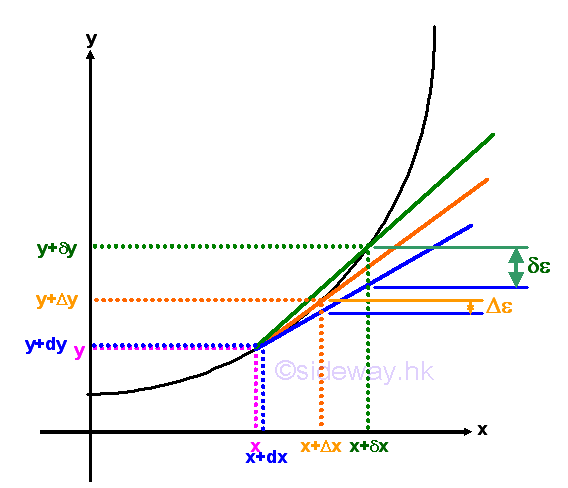
Link:http://output.to/sideway/default.asp?qno=111000013 Linear Approximation Linear Approximation RatioThe previous interpretations of a derivative focuses on the position of a point by taking the limit approaching zero. In other words, the derivative of a function at a point is the most accurate approximation to the rate of change of the function at the point. Therefore the derivative of a point can be used as the linear approximation ratio or the slope of a linear function to approximate the change in a function near the point of differentiation. The accuracy of linear approximation is high when the distance away from the derivative of a point is small, i.e. δε>Δε>0
Approximation CalculationIn some practical applications, problems may be finding the change or the solutions can be approximated by a small change of the known result.
Function Approximation ProblemThe value of a function of a variable can be approximated by a function of known parameter value when the difference between the variable and parameter is small. For example, cubic root of 28. Let function y be cubic function of a variable p. A known parameter of function is 27 and the knwon solution is 3. Therefore the solution of cubic root is 3.0366 and the approximation is:
Error Estimation ProblemMeasuring error is the variation in mesurements. Error is the difference between the measured value and the true value of the meausred object. The result of measuring error can be estimated by derivative. For example, the maximum error of measuring the surfare area of a circular plate, when the measured diameter is 10 and the maximum meausring error is 0.1 is, 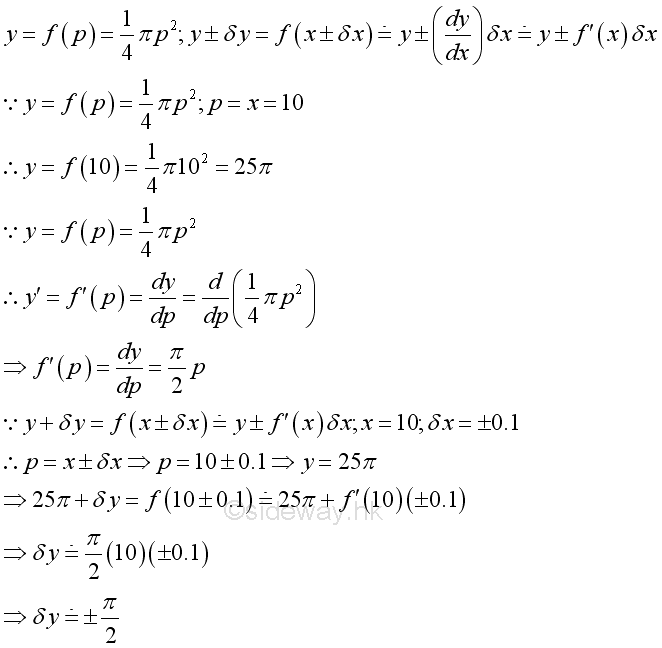
Change Determination ProblemIn others word, the approximation determined by derivative can be the final change or the change. Therefore the derivative can also be used to estimate the initial value by determinating the change. For example, square of 24.9. Let function y be square function of a variable p. A known parameter of function is 25 and the knwon solution is 625. Therefore the solution of square of 24.9 is 620.01 and the approximation is: 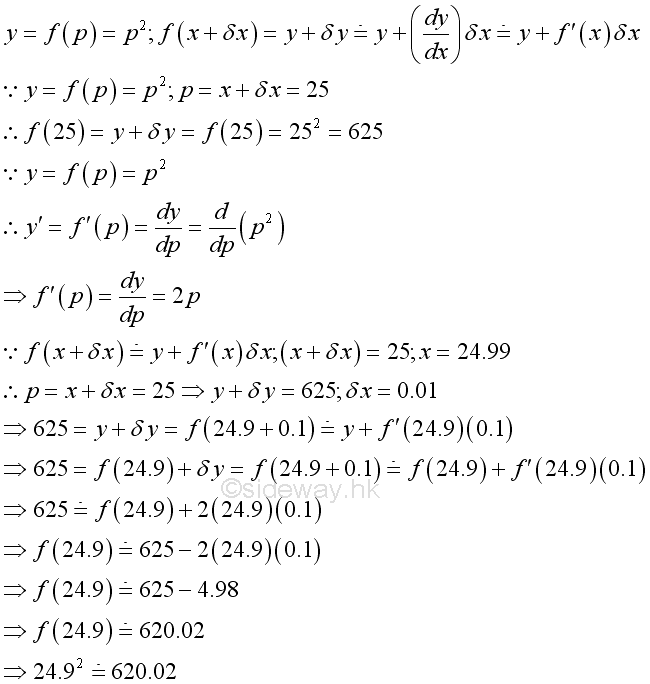
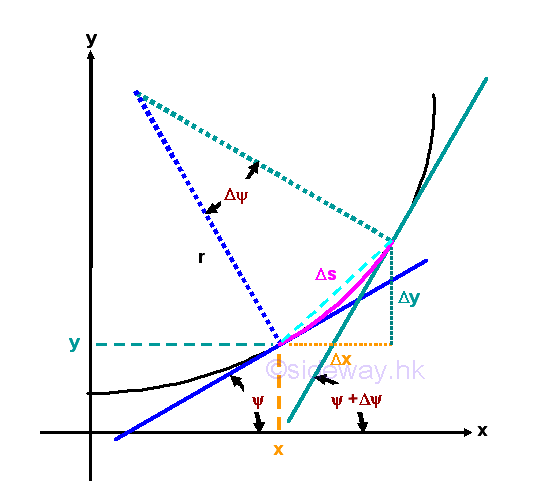
Link:http://output.to/sideway/default.asp?qno=111000015 Curvature CurvatureOne of the typical application of derivative is curvature. By definition, the simplest form of curvature k at a given point on a curve is the rate of change of the tangential angle ΔΨ between tangents with respect to the arc length Δs.
CurvatureMathematically:
Assume the radius of circle at the given point is r. Geometrically:
This implies the curvature of a curve at a given point equal to 1/radius. The radius is an intantaneous radius of the curve at the given point. If the curve is a circle, the curvature at all point is the same and is equal to 1/radius of the circle. Radius of CurvatureTherefore, a circle of the same curvature can be constructed at any point along the curve and this circle is known as the circle of curvature of the curve at the given point. The radius of the circle at the given point is always normal to the curve. This radius is called the radius of curvature of the curve at the given point and is denoted by ρ. Imply
Since both Gs and GZ are functions of x and as Gx approaching 0, both Gs and GZ approaching 0 also, imply the radius of curvature can be expressed as,
For the arc of ΔΨ ,as Δx approaching 0, arc of ΔΨ can be approximated by chord of ΔΨ , Applying Pythagorean theorem, imply
As Δx approaching 0, take limit.
For the angle ΔΨ, the angle can be expressed as the slope of the given point at (x,y), tan Ψ and is equal to the derivative, dy/dx of the function at the given point, imply:
Differentiating the equation with respect to x to get the dΨ/dx, imply 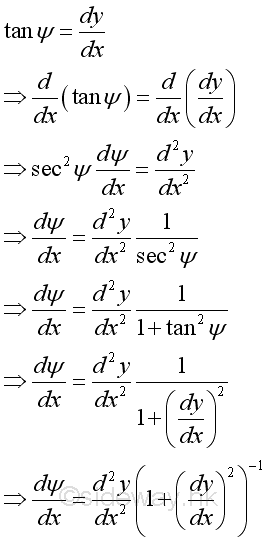
Therefore the radius of curvature in terms of x and y is 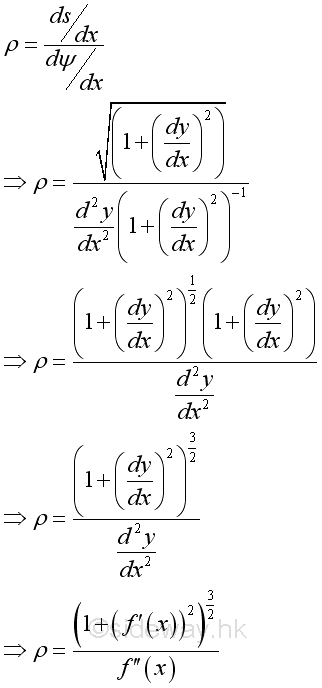
And the curvature in terms of x and y is 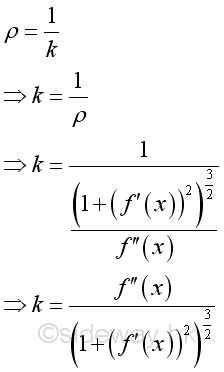
|
Sideway BICK Blog 16/10 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||