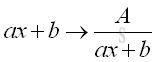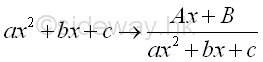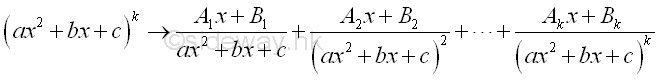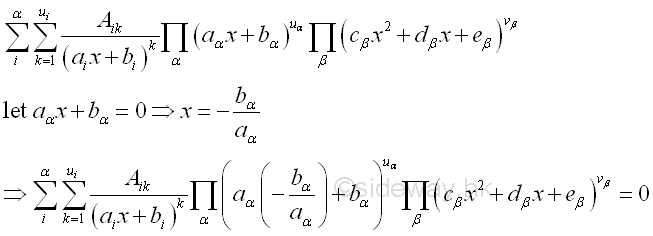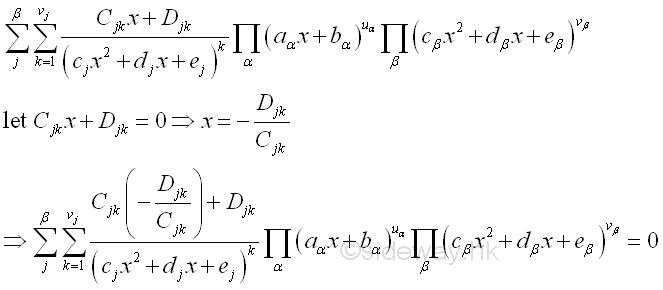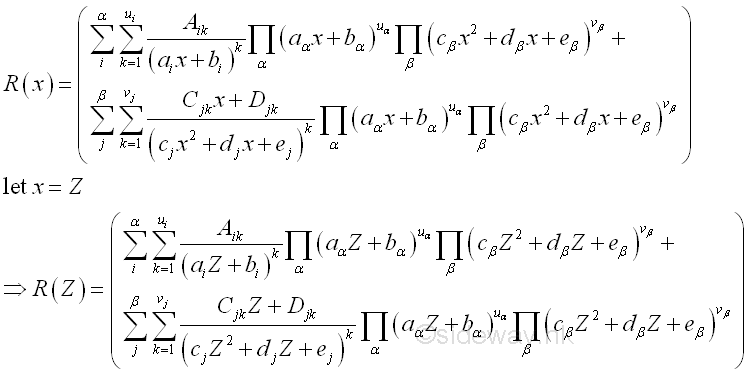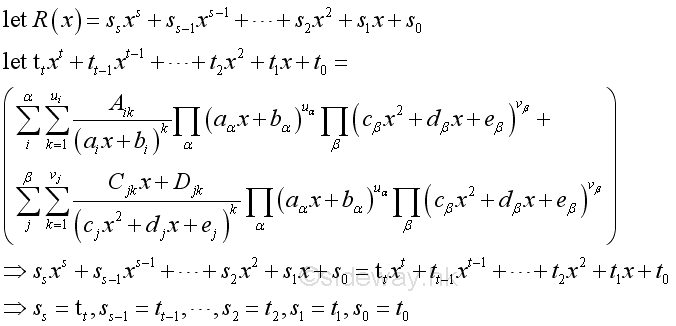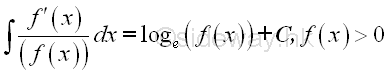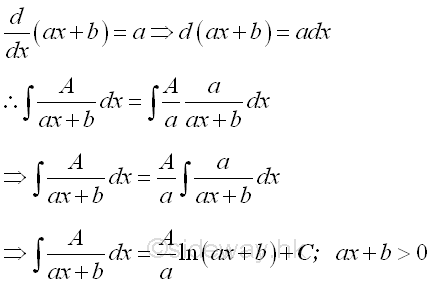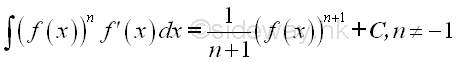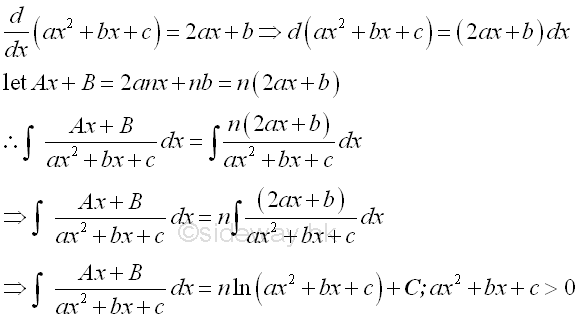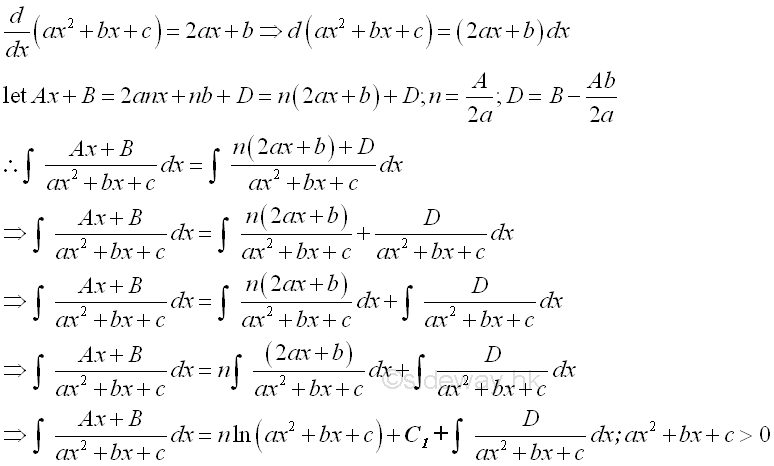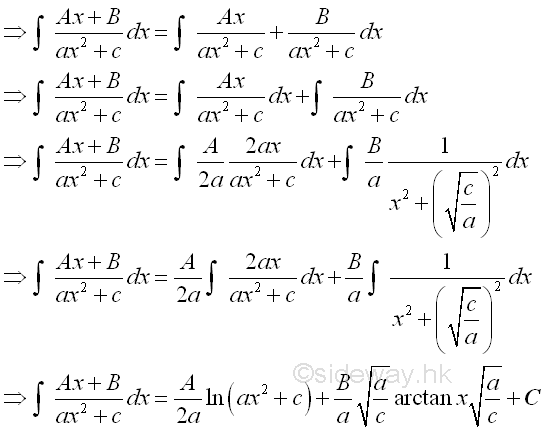Rules of Integration for Indefinite Integral

In order to simplify the task of finding integrals, some integration techniques are developed to help finding integrals by transforming the integral into two parts.

Integration by Parts for Indefinite Integral

Integration by part is method of transforming the original integral of product of two functions into two integrals for taking the advantage of substitution or transformion of the integral to an easier form to continue the integration. The strategy is to simplify the integral by transforming the original integral into two parts which allowing the integration to be continued in other easier way. The technique is making use of the Rule of Product of Functions in differentiation. i.e.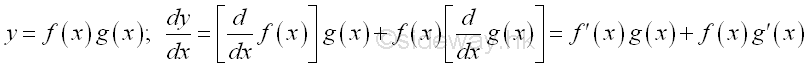

Imply

Integration by Parts:

The strategy of the method is making use of Rule of Product of Functions in differentiation for transforming the integral to two suitable formats to continue the integration.

As in reverse substitution, the formula is assumed the substitution is already there, but through the formula of transformation, the assumed substitued function is changed from the first function to the second or vice versa. In other words, the assumed substitued function becomes selectable after the transformation processes. The two processes of transformation are:

Substitute back. Imply:

The two functions of the original integrand are interchangable because of the cummutative property of function multiplications. The strategy of the method is making use of the applying of the differentiation operation to one function and the integration operation to the other function in the original integrand so that the integration of the transformed integrand can be continued.

Besides through variable of integration transformation, the formula can be applied for single function also and therefore the integration by parts can be used as formula for the interchanging of variable of integration, imply

Techniques of Integration by Parts:

1. Single Function.

   Method of integration by parts can also be applied for single function by assuming unity as the second function. Imply

   

   Sometimes the creation of x may help to continue the integration process.

2. Integrand with one function can not be integrated by ordinary means and one function can be integrated by normal means.

   Let u be the function which cannot be integrated by ordinary means. And let w be the function that can be integrated by nomral means. Imply

   

   This is the basic idea of integration by parts of making the integration can be continued.

3. If both functions of Integrand are integratable, and one of the function is a function of powers of x, in which the power is positive integer.

   Let u be the function of power of x. And let w be the other function. Imply

   

   The function of power of x with positive integer can be eliminated by repeating the application of integration by parts process.

4. If both functions of Integrand are integratable, and one of the function is a function of powers of sin x or cos x.

   The power of  sin x or cos x can be converted using basic trigonometric identities into linear algebraic expression in terms of sin and cos that the integration by parts can be applied. The basic trigonometric identities are

   

   After thAfter the convertion, the function with powers of sin x or cos x become integratable.

5. If the original integral occurs in the result of integration by parts, then the integral can be obtained by algebraic methed indirectly.

   Sometimes the original integral occurs in the result of integration by parts after repeatedly using integration by parts, imply

   

   Therefore the integral can be obtained by algebraic method, imply

   

6. If the integral is a power of sin or cos function in which the power is positive integer.

   The techniques 4 and 5 of integration by parts can be applied.

   1.  power of sin function in which the power is positive integer, imply

      

   2.  power of cos function in which the power is positive integer, imply

      

Rules of Integration for Indefinite Integral

Method of Partial Fractions for Indefinite Integral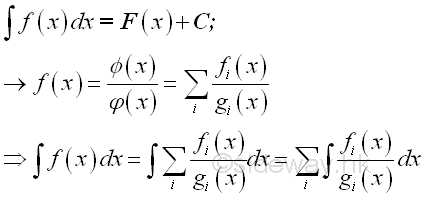

where Φ(x) and φ(x) are rational, integral, algebraical functions of x

The integrand after denominator factorization is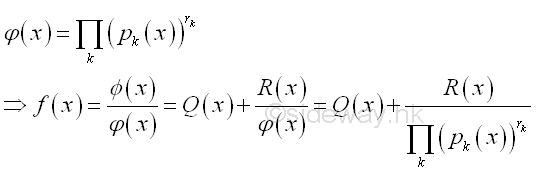

Partial Fractions Expansion

The expansion of partial fractions is the process of converting the factors in the denominator to a sum of terms in which the denominator is determined by the denominator factors and the numerator is undetermined. Before proceeding the expansion, like terms of the factored denominator should be grouped in power form. The grouped terms in the denominator can be classified into two catalogues, linear term and quadratic term. The expansion of factor in each catalogue is governed by two rules.  And the rules are summerized as following:

1. For a linear term ax+b, the format of the partial fraction expansion is

   

2. For a group of repeated linear term (ax+b)k, the pattern of the partial fractions expansion is

   

3. For a quadratic term ax2+bx+c, the format of the partial fraction expansion is

   

4. For a group of repeated quadratic term (ax2+bx+c)k, the pattern of the partial fractions expansion is

   

When letting k=1, the first and the third rules can be considered as the special case of the second and fourth rules respectively.  In general, the factors in denominator can be rewritten as:

Therefore the integrand after partial fractions expansion is

Coefficients Determination:

After the factor expansion, a set of unknown coefficients A, C, D, are needed to be determined. These unknown coefficients can be calculated because the two sides of the equation. Therefore if the denominator on both sides of the equation are identical, the numerator on both sides of the equations are identical also. This can be achieved by ignoring the quotient function and considering the remaining rational function only.: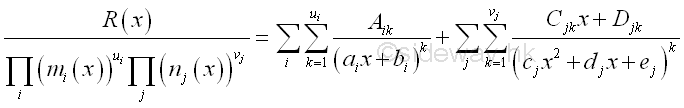

Since the denominator on the left side is the least common factor of the denominator on the right side, the equation of numerator can be obtained by cross-multiplying.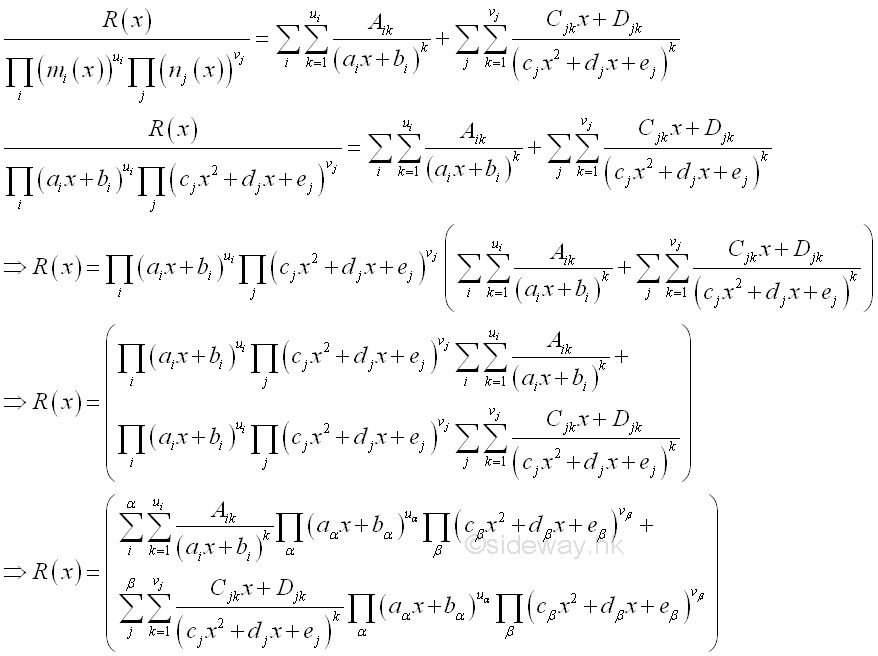

Therefore the coefficients can be determined by the equation of numerator. There are two methods to determine the coefficients:

1. Method of deducing coefficient

   The strategy of this method is to make some terms of the numerator equation on the right side vanish by substituting convenient values.

   Since all quadratic terms of partial fractions are irreducible, the deducing method is applied to the linear terms of partial fractions only.  Imply coefficients can be deduced by substituting different values for x into the numerator equation.

   Since roots of the original denominator can make the partial factor equal to zero, roots of the original denominator are the values of x for deducing coefficient. Imply

   

   Besides, substiting suitable valves of x to the linear terms of quadratic factor can also make some quadratic factors on the right side of numerator equation equal to zero and vanish. Imply

   

   If the number of equation formed by direct substituting convenient value is less than the number of total undetermined coefficients. A simple value of x ,e.g. x=0, 1 can be used as the substiuting convenient value to create the necessary numbers of equations with minimum calculation work needed. imply

   

2. Method of comparing coefficients

   The strategy of this method is to compare the coefficients on each degree of the polynomial on both sides of the numerator equation by expanding the numerator equation on the right side and grouping like terms together to determine the coefficients of each degree so that the coefficients on both sides can be compared degree by degree accordingly. Imply

   

   If the number of equation formed by comparing coefficients is less than the number of total undetermined coefficients. A simple value of x ,e.g. x=0, 1  or convenient values can be used as the substiuting convenient value to create the necessary numbers of equations with minimum calculation work needed as in method of deducing coefficient.

Techniques of Computing Coefficients

In short, the method of deducing coefficient is the indirect generation of equation of coefficient through substiting convenient values to the numerator equation and the method of comparing coefficients is the direct generation of equation of coefficient through equating the coefficients on both sides of the numerator equation.

The strategy of applying these two techniques is similar to solving simultaneous linear equations of multiple variables. The simultaneous solutions set of the system of equation can be determined by using common algebrac techniques, e.g. method of elimination by substitution method, method of elimination by addition. The key differences beween them is the simulatneous linear equations is given while the system of coefficient equation is to be determined. The problem is to generate the useful equations for obtaining unit solution of the  simultaneous linear equations.

The key step of solving simultaneous linear equations of multiple variables is to eliminate number of variable in equations to two, so that these two variables can nullify each other.

The method of deducing coefficients by substituting the root of original denominator can usually obtain simple coefficient equation. And the substition of convenient value 0 is same as determining the zero degree of the expanded equation, constant. Therefore for partial fractions with linear and repeated factors, the method of deducing coefficients is the most effective way to determine the unknown coefficients.

But for quadratic factors, the method of deducing coefficients using root of the original denominator alone does not always done the job. Sometime substiuting convenient value to create the necessary numbers of equations is needed in order to nullify the unknown coefficients. Method of comparing coefficients can usually acts as the complementary tool to complete system of equations by selecting the most suitable degrees of the coefficient equation for coefficient comparing. If there is no root of origninal denominator, the simultaneous equations for determining unknown coefficients can be set up by the method of comparing coefficients. The simultaneous solutions set of the system of equation can then be determined by using common algebrac techniques, e.g. method of elimination by substitution method, method of elimination by addition.

Rules of Integration for Indefinite Integral

Method of Partial Fractions for Indefinite Integral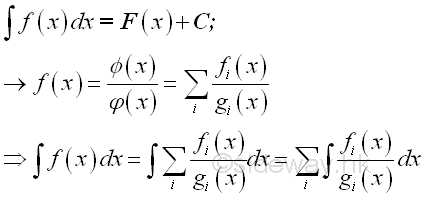

where Φ(x) and φ(x) are rational, integral, algebraical functions of x

The integrand after denominator factorization is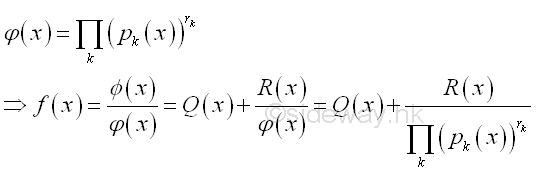

Integration by Partial Fractions

The method of integration by partial fractions can be expressed as

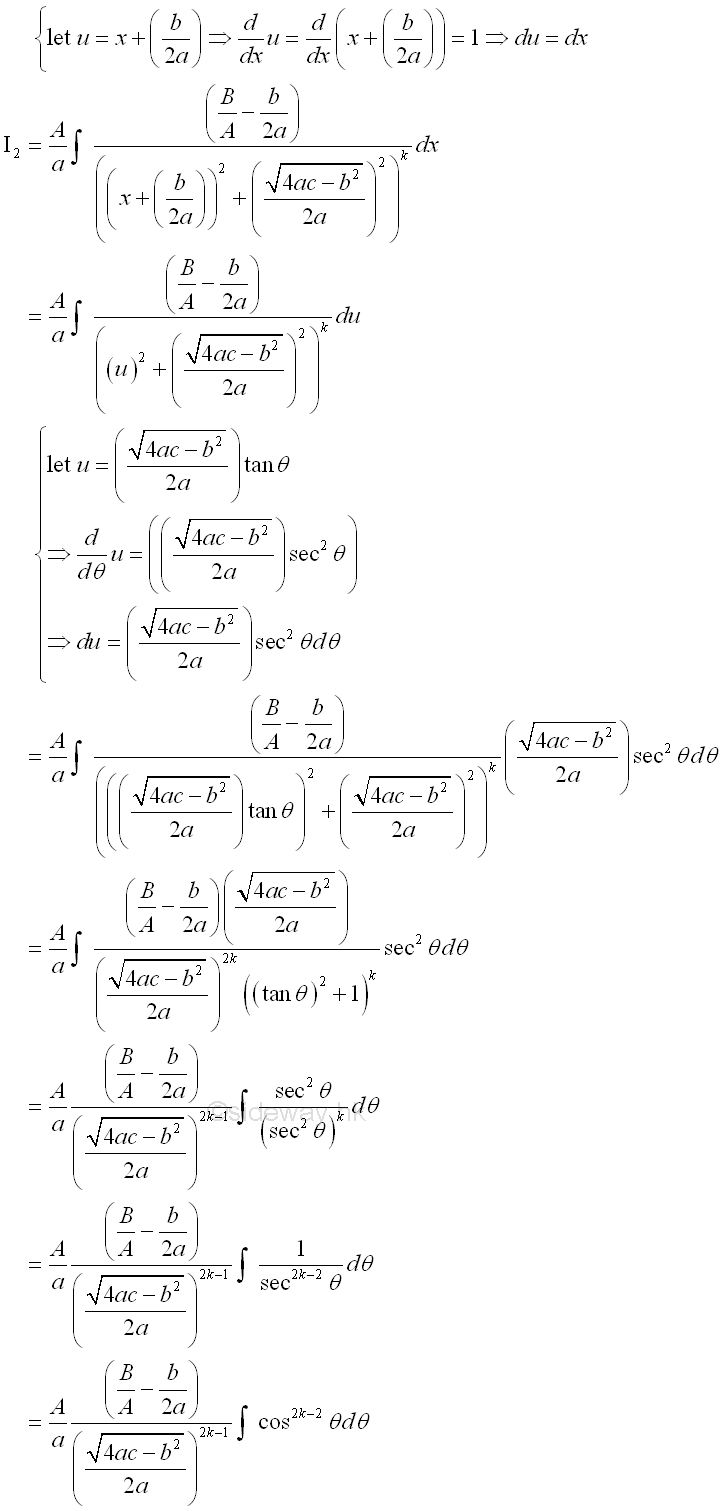
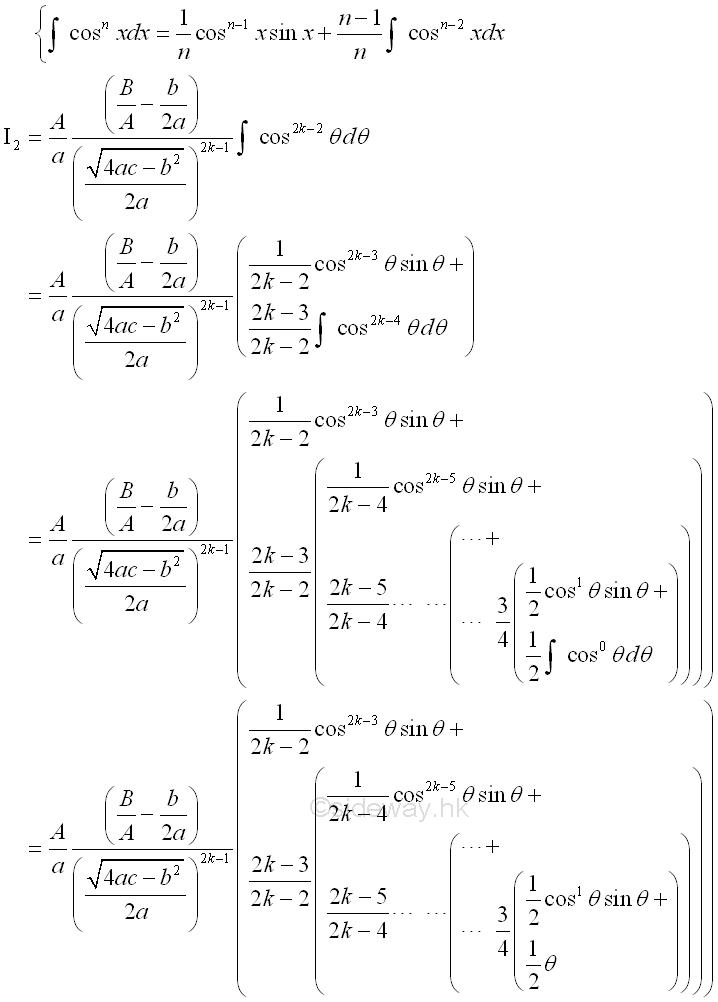
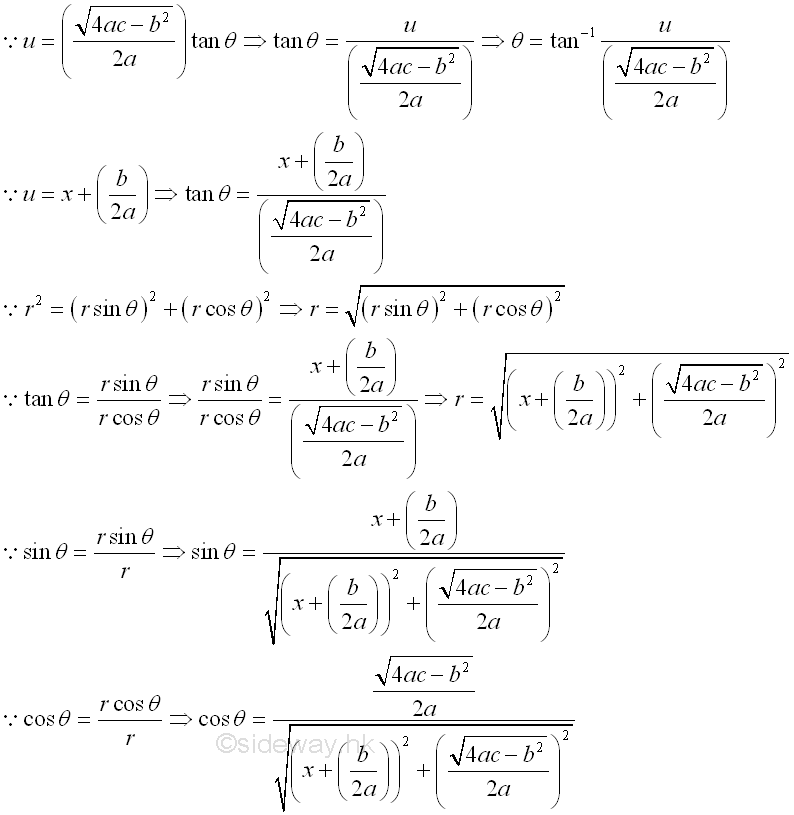
The integral of polynomial Q(x) can be obtained by making use of the constant multiple, sum of function properties of intergration and applying the anti-differentiation of the derivative of polynomial. The integration of the four case of fraction factors after partial fractions are:

1. linear partial fraction A/(ax+b)

   This is the most common type of partial fraction, the integral of the linear partial fraction can be obtained by the quotient of standard functions rule of indefinite integral,

   

   Therefore the integral of linear partial fraction can be determined by:

   

2. repeated linear partial fraction  A/(ax+b)k

   This is the most simple type of partial fraction.The integral of the repeated linear partial fraction can be obtained by product of standard functions rule of indefinite integral.

   

   Therefore the integral of repeated linear partial fraction can be determined by:

   

3. quadratic partial fractionr (Ax+B)/(ax2+bx+c)

   For the quadratic partial fraction, there are some variant forms.

   1. Standard quadratic partial fraction (Ax+B)/(ax2+bx+c).

      1. If the numerator can be expressed as the derivative of the denumerator, imply

         

      2. If the numerator can not be expressed as the derivative of the denumerator, imply

         

         For the last integral, the quadratic factor can be resolved by completing the square, imply

         

         Since the quadratic factor is irreducible, 4ac-b2>0, imply

         

         Therefore the integral is

         

   2. Quadratic partial fraction Ax/(ax2+bx+c). Same as a.ii case where B=0, imply

      

   3. Quadratic partial fraction B/(ax2+bx+c). Same as the last integral in a.ii case where B=D, imply

      
   4. Quadratic partial fraction with quadratic factor, (ax2+bx)

      Quadratic factor (ax2+bx) is same as (ax2+bx+c) by letting c=0, the integral can be obtained as in case a

   5. Quadratic partial fraction with quadratic factor, (ax2+c)

      Quadratic factor (ax2+c) is same as (ax2+bx+c) by letting b=0, the integral can be obtained as in case a. But no complete the square is needed since the factor can be directly transformed into needed format., imply

      

4. repeated quadratic factor  (Ax+B)/(ax2+bx+c)k

   The proceduce of determine the integral is same as case 3 except for the determining of the integral with power after decomposing the original integral into two integrals. Imply

   

   The first integral can be obtained by simple substitution. Imply

   

   The second integral can be obtained by simple substitution. Imply

   

   The second integral can further be expanded using the formule in integration by part as:

   

   The theta angle can be transformed back to x through trigonometry, imply:

   

   And the integral can be expressed as: