 Sideway
BICK BLOG from Sideway
Sideway
BICK BLOG from Sideway
|
Link:http://output.to/sideway/default.asp?qno=140300003 Typical Cases of Tangential Motion Kinematics: Typical Cases of Tangential MotionIn practical engineering problems, there are some typical cases of tangential motion. The object moves in a straight line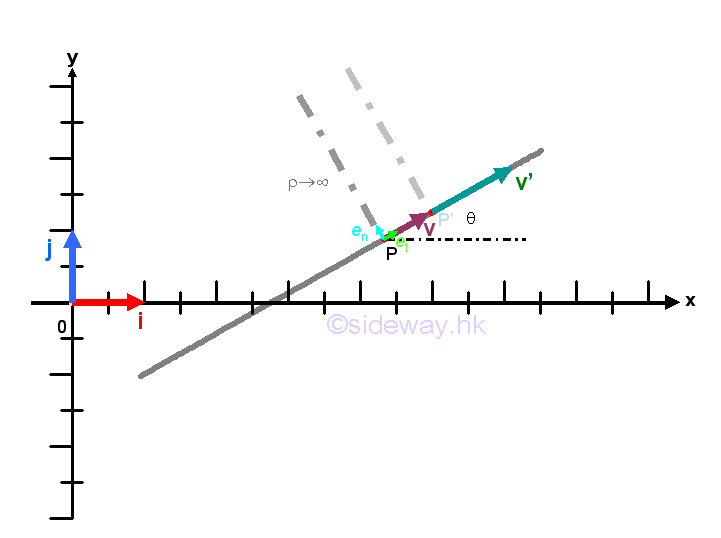
When an object moves in a straight line, the radius of curvature ρ is equal to infinity. Since the normal acceleration component an is inversily propertional to the radius of curvature ρ, the normal acceleration component an is equal to zerol and the acceleration a of the motion is equal to the tangential acceleration componet at only, which is equal to the time rate of change in the magnitude of the velocity dv/dt. In other words, when an object in curvilinear motion, if the radius of curvature tends to infinity, the normal acceleration component of the object approaches zero also. Imply 
The object moves in a curved path with constant speed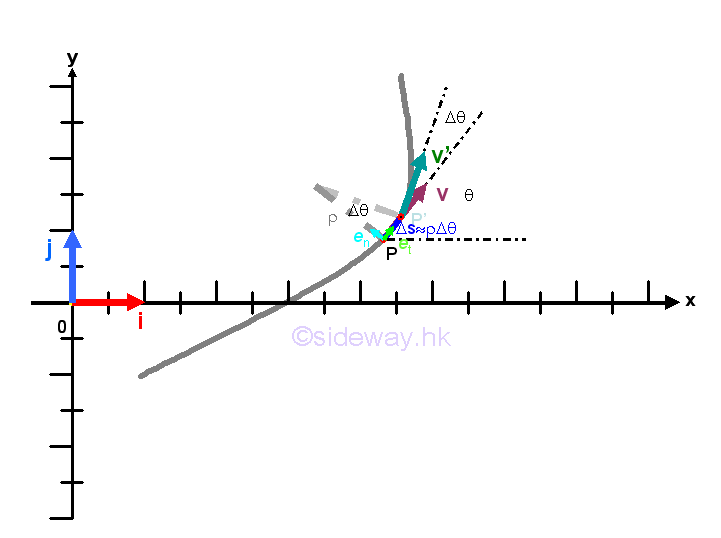
When an object moves in a curved path at constant speed, the tangential acceleration component at along with the tangential velocity component vt which is equal to the speed of the object v, is equal to zero and the acceleration a of the motion is equal to the normal acceleration componet an only, which is equal to the time rate of change in the direction of the velocity. In other words, when an object in curvilinear motion, the normal acceleration component of the object mush not be equal to zero, and the radius of curvature ρ should also be tend to an finite value. Imply 
The object moves in a curved path with constant speed and constant normal acceleration component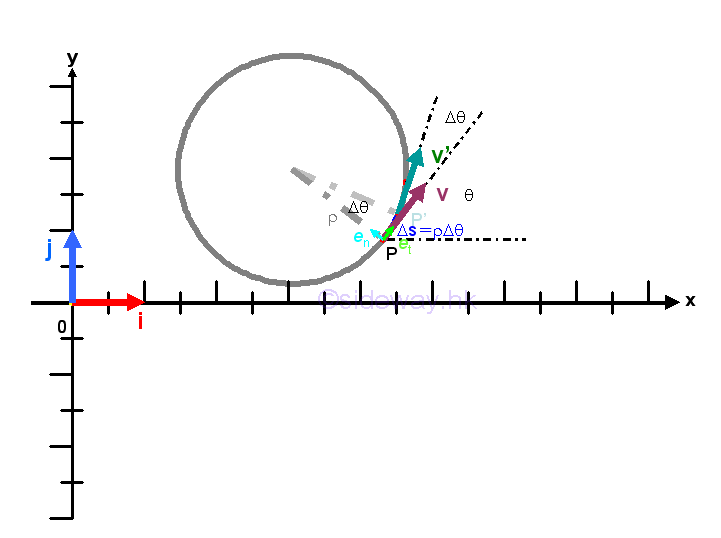
When an object moves in a curved path at constant speed, the tangential acceleration component at along with the tangential velocity component vt which is equal to the speed of the object v, is equal to zero and the acceleration a of the motion is equal to the normal acceleration componet an only, which is equal to the time rate of change in the direction of the velocity. Since the speed of the object is constant, if the normal acceleration component is also a constant, then the radius of curvature ρ should be a constant aslo. In other words, when an object in curvilinear motion, if both the speed and the normal acceleration component of the object are constants, the object is in uniform circular motion with the constant radius of curvature ρ which is equal to the radius of the circular motion. Imply 
For an uniform circular motion, both the radius of curvature ρ and the tangential speed v are constant. Therefore the distance traveled can be expressed in term of the time interval Δt or the change in angle Δθ during time interval Δt. And time interval Δt can then be expressed in term of change in angle Δθ. The change in velocity can also be obtained trigonometrically and be expressed in term of a sine function of change in angle Δθ. By taking limit as the change in angle Δθ approaching zero. the magnitude of acceleration a can then be determined and the direction of the acceleration is always be towards the centre of the circular motion. Imply 
The object moves in a curved path with constant tangential acceleration component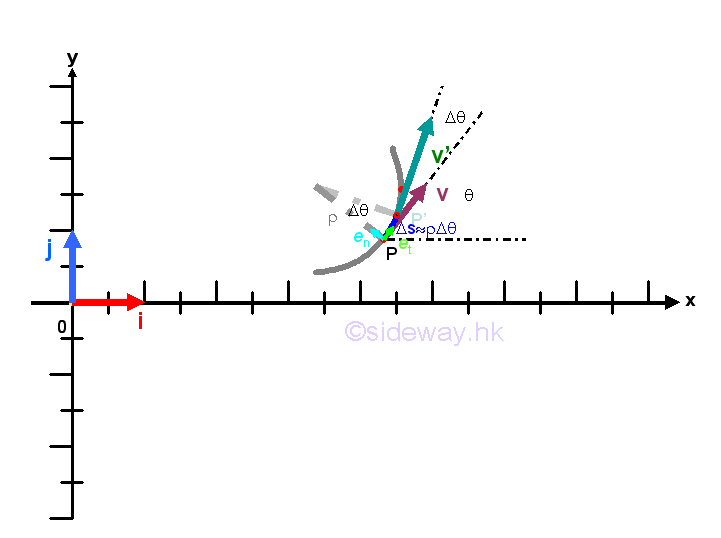
When an object moves in a curved path with constant tangential acceleration component, the normal acceleration component an normal to the tangential velocity component vt should not be equal to zero otherwise the object is in a rectilinear motion. Since there is no normal velocity component vn and the tangential velocity component vt is always along with the motion of the object, the equations of tangential motion are similar to those equations of linear motion. Imply 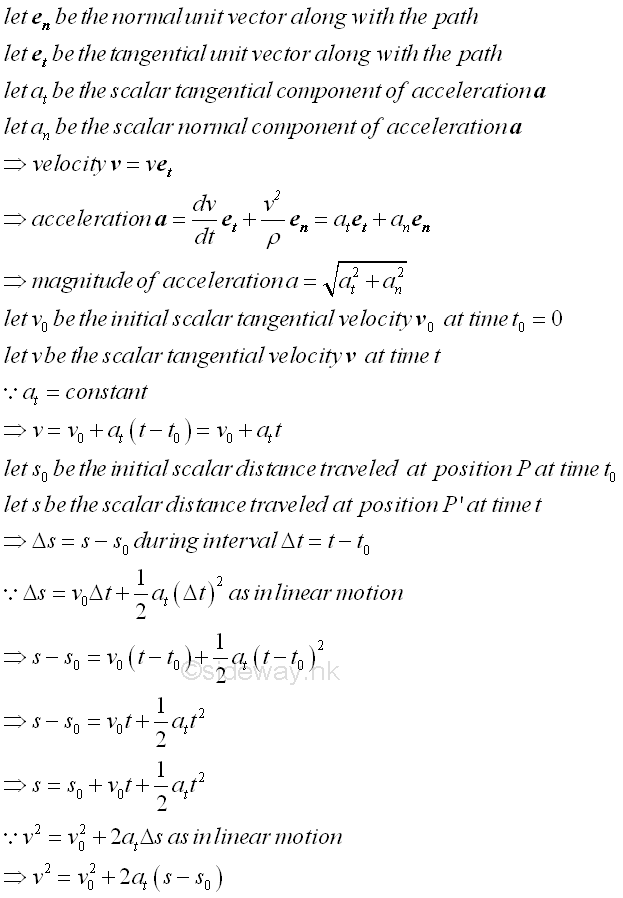
The object moves in a fixed curved path y=f(x), the radius of curvature ρ along the path can be expressed in term of the rate of change of the function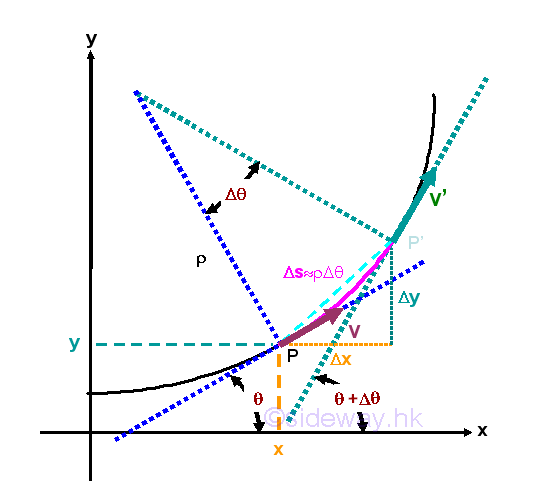
When an object moves in a fixed curved path y=f(x), the radius of curvature ρ along the path can be expressed in term of the rate of change of the function. The radius of curvature ρ can be expressed in term of the rate of change of traveled distance Δs with respect to the angle θ when taking limit as Δθ approaching zero. Since both Δs and Δθ are functions of x also, the radius of curvature ρ can then be expressed in term of the rate of change of the function y=f(x) by making use of the Pythagorean theorem and the slope of the function. Imply 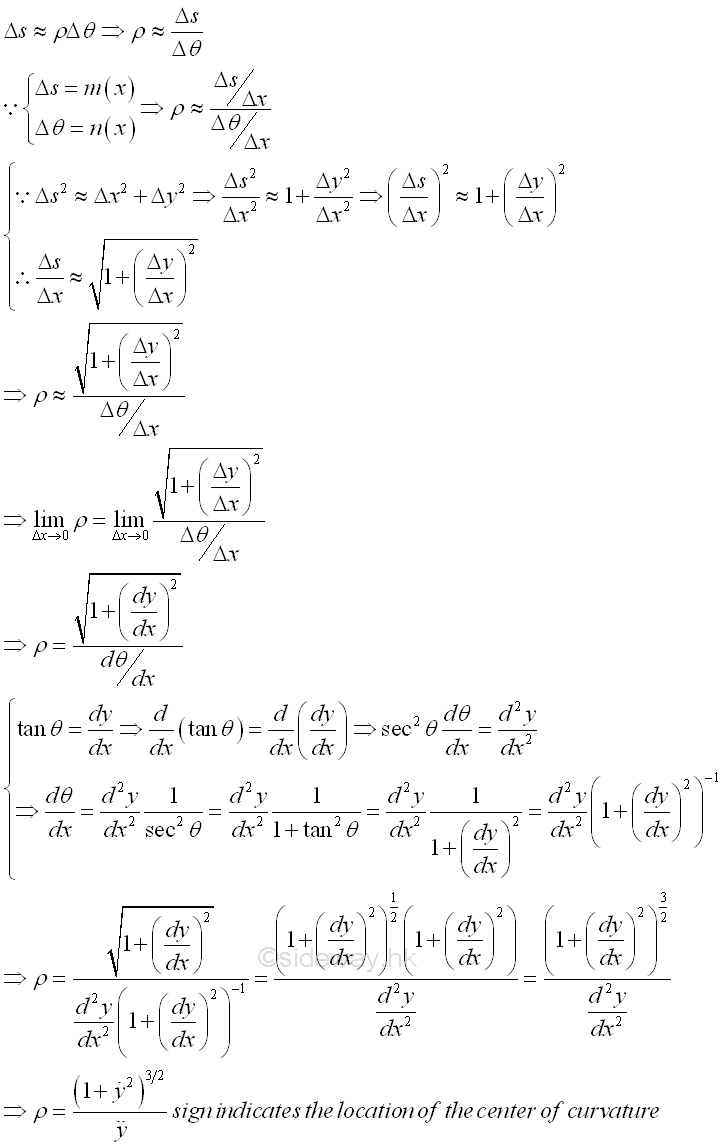
|
Sideway BICK Blog 10/03 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

