Kinematics: Relative Translation Motion

When several objects moving in curvilinear motion, these objects can also be related to each other. Usually, the system of objects are measured by a single time system with the same measurement dimension. However, when objects move in a system more than one dimension, the orientation of object should also be considered because the rate of change of a vector function for an object as observed from a moving object may be different from the rate of change of the object as observed from a fixed frame of reference.

Relative Independent Motion of Two Objects under translation

In simple curvilinear motion, the orientation of an object does not change during the motion along the path. In other words, the object is in translation motions simultaneously along the axes of reference frame of the object which is always parallel to the corresponding axes of a fixed frame of reference.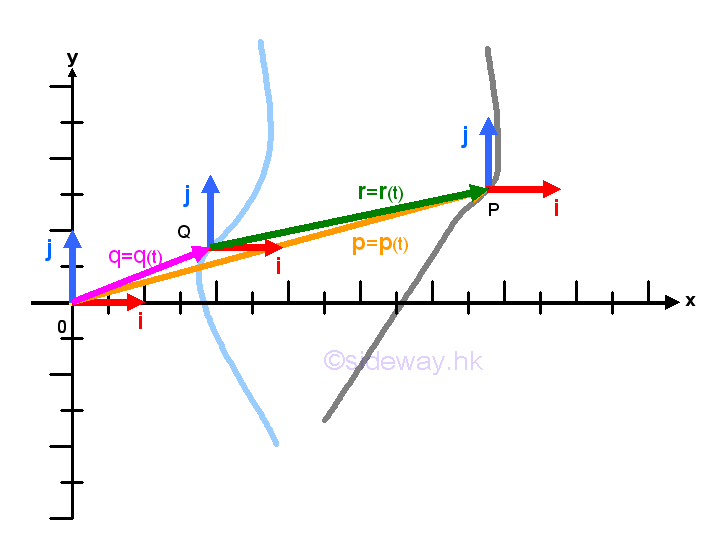  

Since the position vector of a point with respect to the fixed frame of reference, that is the origin O, changes according to the position of the point, the position vector with respect to the fixed frame of reference is also changed with respect to a moving frame of reference. Because the orientation of frame of reference of the moving object does not changed, the relative position of an object as observed from a moving object can be obtained by deducing the position vector of the moving object with respect to the fixed frame of reference from the position vector of the observed target object with respect to the fixed frame of reference as in one dimensional motion. Imply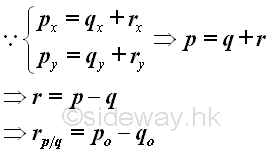 

However, the rate of change of a vector function, observed by the fixed frame of reference, does not change, when the frame of reference of the observing point is in translative motion, where the axes of the frame of reference of the observing point are always parallel to the corresponding axes of the fixed frame of reference.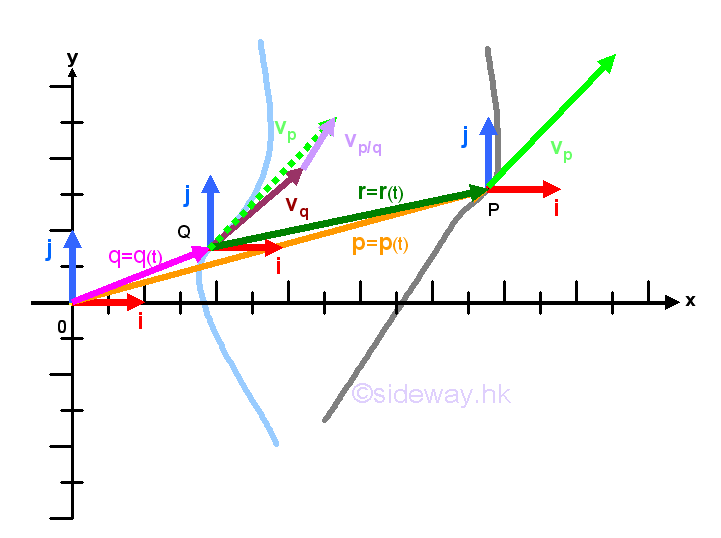

Since the rate of change of a vector at a point with respect to the fixed frame of reference, that is the origin O, is only a relative relationship between two component functions, the rate of change of a vector depends only on the orientation of the frame of reference not the origin of the frame of reference. Therefore the velocity vector does not change when the fixed frame of reference is translated. And thus for objects that are in translation, the relative velocity of an object as observed from a moving object can be obtained by deducing the velocity vector of the moving object with respect to the fixed frame of reference from the velocity vector of the observed target object with respect to the fixed frame of reference as in one dimensional motion. Imply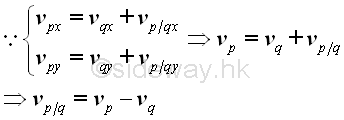 

Similarly, the rate of change of a velocity vector at a point with respect to the fixed frame of reference, that is the origin O, is only a relative relationship between two component functions, the rate of change of the velocity vector depends only on the orientation of the frame of reference not the origin of the frame of reference.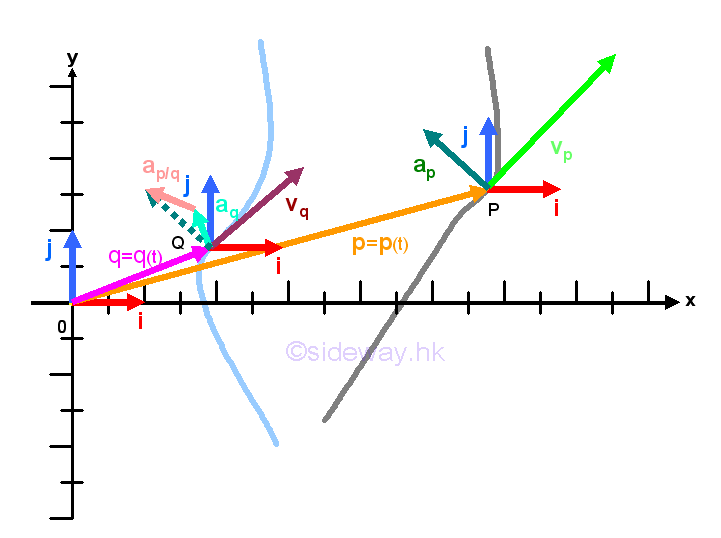

Therefore the acceleration vector does not change when the fixed frame of reference is translated. And thus for objects that are in translation, the relative acceleration of an object as observed from a moving object can be obtained by deducing the acceleration vector of the moving object with respect to the fixed frame of reference from the acceleration vector of the observed target object with respect to the fixed frame of reference as in one dimensional motion.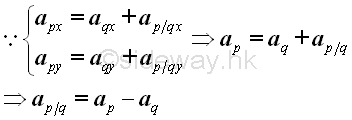 

Inertial Reference Frames

The coordinate system used as the frame of reference to measure the object is called inertial reference frame, which is a rigid system without acceleration such that the Newton's laws of motion are always valid. The surface of the Earth can be considered as an inertial frame for most engineering problems because the daily rotation is quite slow.