Kinematics: Radial Motion and Cylindrical Coordinates

In practical engineering problems, sometimes it is convenient to resolve the component functions of the vector function of motion into components which are the radial and transverse components of the object with respect to a reference origin of the motion together with a longitudinal component or axial motion. Thus the study of the motion can be focused on the motion of an object along the radial direction or perpendicular to the radial direction related to a reference origin. The planar polar motion can be extended to 3 dimensional by adding an axial component to the polar-coordinate system and the coordinates of the new 3D coordinate system is called cylindrical coordinates. 

Component Functions in Cylindrical Coordinate System

There are three independent coordinates  in the cylindrical coordinate system. The coordinates are radial distance component, angular direction component, and longitudinal distance component. In curvilinear motion, when the vector function of motion is resolved into component functions that are radial, transverse and longitudinal to the reference origin of motion, the orientation of the frame of reference of the object changes during the motion along the path. In other words, the frame of reference of the object is in translative and rotational motions simultaneously along the path of motion. In this case, the position of the object is more convenient to be defined by its cylindrical coordinates R, θ, and z instead of rectangular coordinates x, y and z. In fact, the vector sum of the coordinate components for positioning in cylindrical coordinate system and rectangular coordinate system are the same.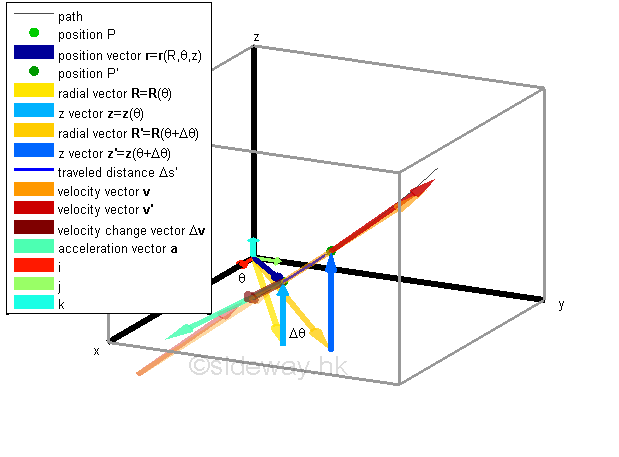  

Since the velocity vector of the motion is alway tangent to the path, the vector function of the velocity vector usually have radial, transverse, and longitudinal velocity components. Similarly the vector function of the acceleration vector also usually have both radial, transverse and longitudinal acceleration components such that the speed of the radial velocity vector can be accelerated by the radial component of the acceleration vector, the direction of the radial velocity vector can be accelerated by the transverse component of the acceleration vector and the longitudinal velocity can be accelerated by the longitudinal component of the acceleration vector.

Unit Vectors in Cylindrical Coordinates

Let the unit radial vector of the velocity vector v be er ,the unit transverse vector of the velocity vector v be eθ and the unit longitudinal vector of the veloctiy vector v be k at position P with reference to the origin O. Unlike the unit vectors i and j of the fixed frame of reference, the unit vectors er and eθ are translated and rotated simultaneously along the path of the motion while unit vector k remains unchange. Sometime the frame of reference used by the observer at the reference origin is more convenient to have the same type of frame of reference. In this case, the position of the object can also be expressed in term of the unit radial vector er and the unit transverse vector eθ also. 

Geometrically both the unit radial vector er and the unit transverse vector eθ can also be expressed in terms of the unit vectors i and j of the fixed frame of reference by triangle rule.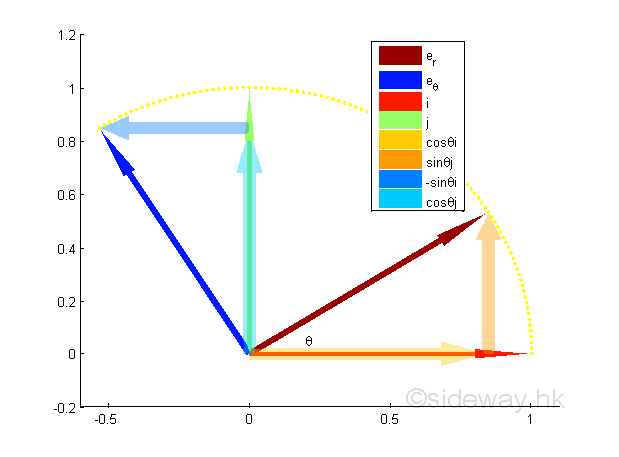

Position Vector in Cylindrical Coordinates

Let the motion of an object at position P is of radial distance R with an angle of θ relative to the x-axis of the fixed frame of reference, and of longitudinal distance z with reference to xy plane at an instant of time t. The position vector r of the object can then be expressed in term of the unit radial vector er ,the unit transverse vector eθ  and the unit vector k also. Since the radial position vector of the object always aligns with the unit radial vector er, the radial position vector can be expressed in term of  the unit radial vector er only, that is rer. Besides, the longitudinal position vector of the object always aligns with the unit longitudinal vector k, the longitudinal position vector can also be expressed in term of the unit longitudinal vector k only, that is zk.  Imply

Velocity Vector in Cylindrical Coordinates

Since the motion of the object can be resolved into radial, transverse and longitudinal motions, the displacement, velocity and aceleration can also be resolved into radial transverse and longitudinal components accordingly. However as the frame of reference of the radial and transverse components translate and rotate along with the motion except the longitudinal components, the component of the motion function cannot be obtained from the corresponding component of the change of the related motion function directly as in the fixed frame of reference because the frame of reference rotates along the path of motion besides translating. This is because the method of vector decomposition used in the vector addition with respect to a fixed or translated frame of reference cannot be applied in the case of the addition of vectors with respect to a rotated frame of reference. In other words, the velocity components cannot be obtained from the position vector components directly.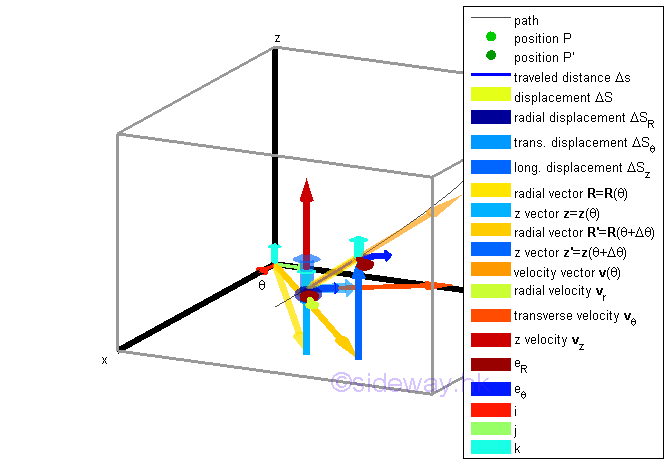

That is, the displacement of the object with radial position vector rer is equal to a displacement vector function with radial and transverse components instead of only radial component because the frame of reference of the position vector at the end of the motion at position P' is rotated with respect to the frame of reference of the displacement vector although both position vector and displacement vector have the same frame of reference at the beginning of the motion at position P. However, as the frame of reference of a velocity vector is always same as the displacement vector, the component functions of the velocity vector can be obtained directly from the corresponding components of the displacement vector.  While the acceleration vector of the motion is similar to the case of displacement vector. Since the frame of reference for the longitudinal component does not changed with respect to time, all components of displacement, velocity and acceleration can be obtained directly as in rectangular coordinate system. 

Acceleration Vector in Cylindrical Coordinates

By definition, the velocity vector function of a motion is equal to the rate of change of the displacement vector function, therefore the velocity vector function of a motion can be derived from the displacement vector function directly. And by definition,  the acceleration vector function of a motion is equal to the rate of change of the veclocity vector function, therefore the velocity vector function of a motion can be derived from the displacement vector function using differentiation also.  Imply

Unit Vector Derivatives in Cylindrical Coordinates

Graphically, the rate of change of a radial unit vector er with respect to the angle θ and the rate of change of a transverse unit vector eθ with respect to the angle θ  are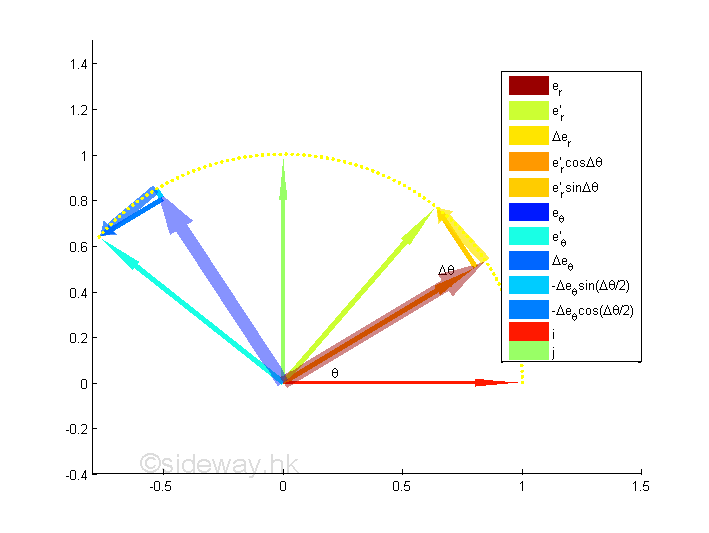

Both the changes of the radial unit vector er and the transverse unit vector eθ , Δer and Δeθ, can be obtained by vector addition as in determining the displacement vector from the position vectors. Based on the frame of reference at time t, the frame of reference rotates clockwisely by angle Δθ during the time interval Δt. Since the radial magnitudes of a radial unit vector er and a transverse unit vector eθ are always equal to a constant, the formed triangles are isosceles triangles with both Δer and Δeθ, are the base of a triangle. The rate of change of the radial unit vector er and the transverse unit vector eθ can be obtained as following using two different approaches. Imply

Motion Functions in Cylindrical Coordinates

Therefore the motion function of an object can be determined as following.

Typical Case: Cylindrical Motion

When an object in cylindrical motion, moves along a cylinder, although the object with position vector r=ReR+zk moves along a cylinder, the radial component function R of the position vector of the motion is always equal to a constant, that is R=constant. Since R is equal to a constant, both the first derivative and the second derivative of function R are equal to zero also. And the motion functions of a cylindrical motion are

Direct Differentiation of the Radial and Transverse Unit Vectors

Since both the Radial and Transverse Unit Vectors can be expressed in term of the unit vectors i and j of the fixed frame of refenece also, the derivative of the Radial and Transverse Unit Vectors can be obtained by direct differenctiation. Imply