Kinematics: Rate of Change of a Vector Function

A vector function with a single variable, time t can be used to describe the motion of an object in 2 or 3 dimensional space. Because of the properties of the derivative of a vector function, rate of change of component functions of a motion along rectangular coordinate axes, x, y, z, can be determined accordingly.

Vector Function of the Position Function of Motion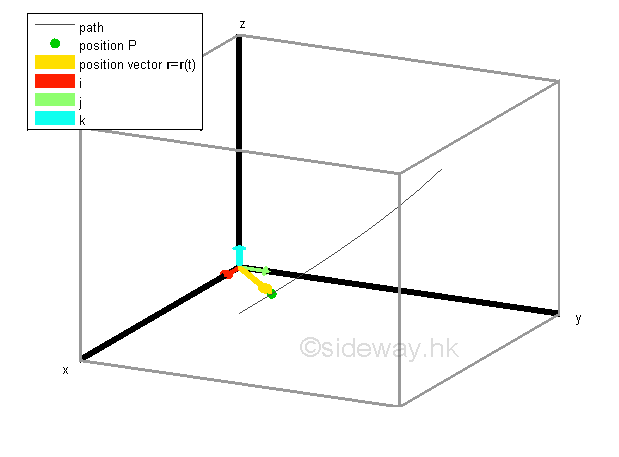

In kinematic 3D motion, the position P of an object can be expressed in term of a vector function which depends on a single parameter, time t, that is r=r(t). Since a vector function r=r(t) can be resolved into component functions along the rectangular coordinate axes x, y, z, the motion of the object can be described by the position function along the coordinate axes independently.

Vector Function of the Velocity Function of Motion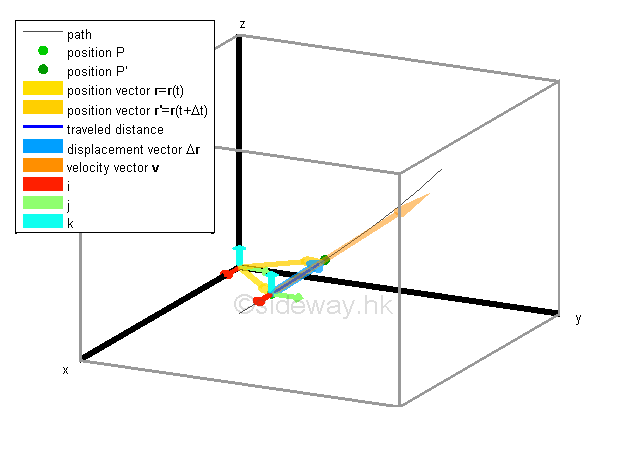

By definition, the rate of change of a vector function of the position function is equal to the velocity function of motion. From the properties of the derivative of vector function, The vector function of velocity functon of motion can be obtained by differentiating the vector function of the position function of motion and a single dot is used to indicate the first derivative of the position function. Imply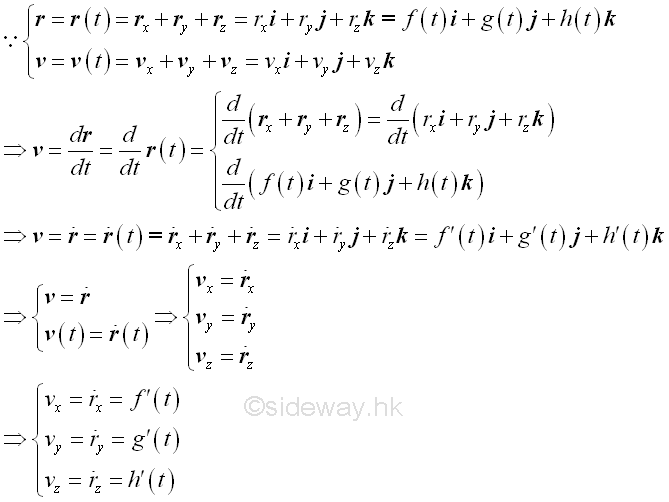

Vector Function of the Acceleration Function of Motion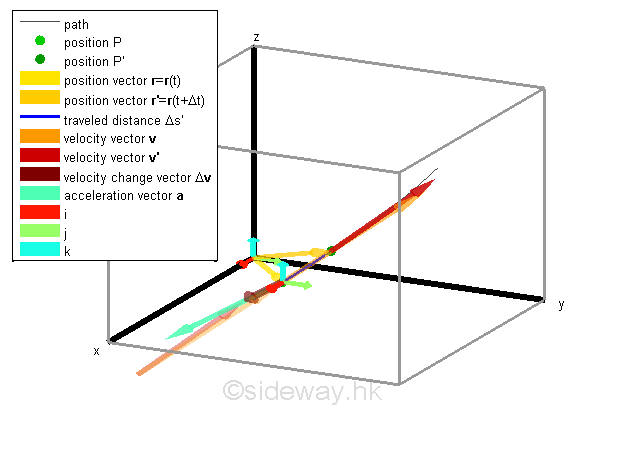

By definition, the rate of change of a vector function of the velocity function is equal to the acceleration function of motion. From the properties of the derivative of vector function, The vector function of acceleration functon of motion can be obtained by differentiating the vector function of the velocity function of motion and a single dot is used to indicate the first derivative of the velocity function. Since a velocity function can be obtained from a position function, therefore a double dot is used to indicate the second derivative of the position function. Imply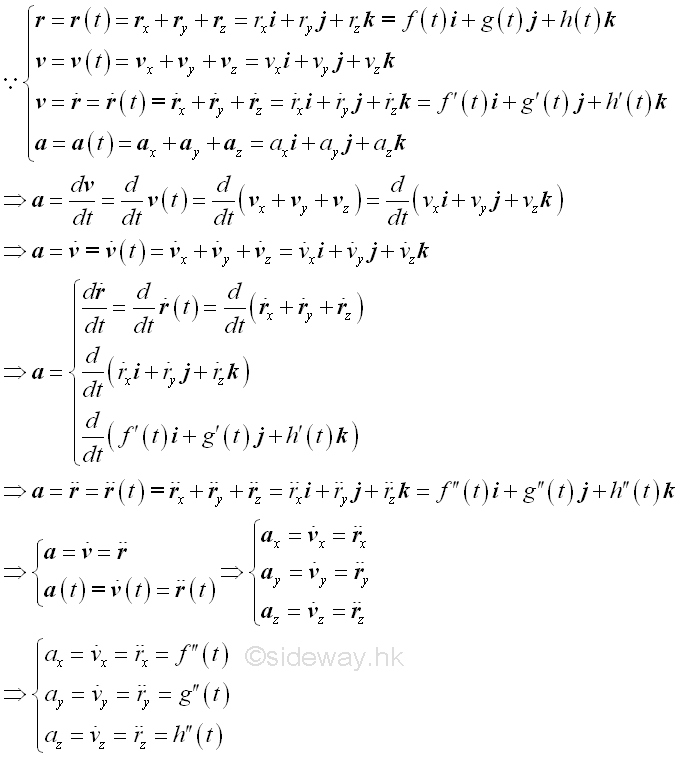

Examples of 3D Kinematics

A particle moves in 3D Cartesian coordinate system can be expressed in terms of the rectangular coordinates, x, y, and z, using the unit vectors, i, j, and k, which is similar to the moton of an particle moves in 2D Cartesian coordinate system. The motion of a particle can be described by a position vector, r with respect to time t, e.g. r(t)=(sin(t)+0.2)i+(cos(t/2)j-0.2)+tk. The motion of the particle is