Prime Number

Prime numbers are natural numbers, e.g. 2, 3, 5, 7,..., which can only be divided by 1 and itself. For other natural numbers, neither 1 nor prime number, they are called composite numbers. In general, a composite number can be expressed as a product of two factors, i.e. n=xy. 1 is not a prime because 1 can only be divided by 1 and 1 has one divisor, 1 only. Besides, prime numbers are always positive numbers. And 1 and 0 are neither prime nor composite. One important relationship between prime number anf composite number is stated in the Fundamental Theorem of Arithmetic, that is every natural number except 1 can be represented by a product of one or more primes uniquely. In other words, natural number except 1 is either prime or composite that can be factored as a product of primes in one unique way.

Infinitely Many Prime Numbers

"There exist infinitely many prime numbers" as there are infinitely natural numbers on the number line. Many supporting proofs can support the existence of infinitely prime numbers along the number line.

Euclid's Method (c 300 BC)[1]

Since there are infinitely natural numbers, if there is a composite number, N, i.e. N=p1p2p3..., formed by the product of some known existing prime numbers, e.g. p1=2< p2=3<p3<...<pi...,  there always exists a number formed P by N+1. From the fundamental theorem of arithmetic, if P is a composite number and P is divisible by prime number p, then p must not be any of the known existing prime numbers, p1, p2, p3<,...., otherwise the prime number p would divide the difference of N and P that is equal to 1. This is impossible because 1 is only divisible by 1 and is not a prime and implies that p is still another prime number not known. If P is a prime number, then P is already another prime number not known and similarly. As there are infinitely natural numbers, by repeating the process, there exists infinitely many prime numbers.

Similarly, this is also true for the product of some primes minus one

Kummer's Proof (1878)[1]

Assume that there are only finitely many prime numbers, p1< p2<p3<...<pi...<pn, a composite number N can be formed by the product of all known existing prime numbers. i.e. N=p1p2p3...pi...<pn and the composite number N is greater than 2. There always exists a number N-1. According to the Fundamental Theorem of Arithmetic, N-1 always has at least one prime factor p, which is also a common prime factor of N.  As shown in Euclid's Method, p divides (N-1)-N=-1 is impossible.

Stieltjes's Proof (1890)[1]

Similar to Kummer's method, assume that there are only finitely many prime numbers, p1< p2<p3<...<pi...<pn, and a composite number N can be formed by the product of all known existing prime numbers. i.e. N=p1p2p3...pi...<pn. Instead of creating another number, the number N is factored according to the Fundamental Theorem of Arithmetic into two factors m and n where m and n is greater or equal to 1. Since pi in the finitely prime number set can only divide either m or n, but not both number m and n. Let P =m+n. Since m+n is not equal to one, therefore P cannot be divided by any of the existing primes which is absurd as there must be at least one new prime factor for the number P, i.e. m+n,

Goldbach's Proof (1730)[1]

Besides the proof by contradiction, Goldbach prove there are an infinitely many prime numbers by constructing an insequence sequence of pairwise relatively primes, p1, p2, p3,..., pi,..., pn,  without a common prime factor from an infinite sequence of natural numbers, a1, a2, a3,..., ai,..., an, greater than 1. In general, if pi, is a prime dividing ai, then p1, p2, p3,..., pi,..., pn are all different. The greatest common divisor can be calculated by the successive euclidean divisions and no knowledge of the prime factors of the numbers is required. Infinitely sequence of Fermat numbers are used by Goldbach in the proof of infinitely many prime numbers. Lemma of the Fermat numbers Fn=22n+1 are pairwise relatively prime for n≥0. The pairwise relatively prime property of Fm-2=F0F1...Fm-1 for n≥1 can be proved by induction and contradiction. Imply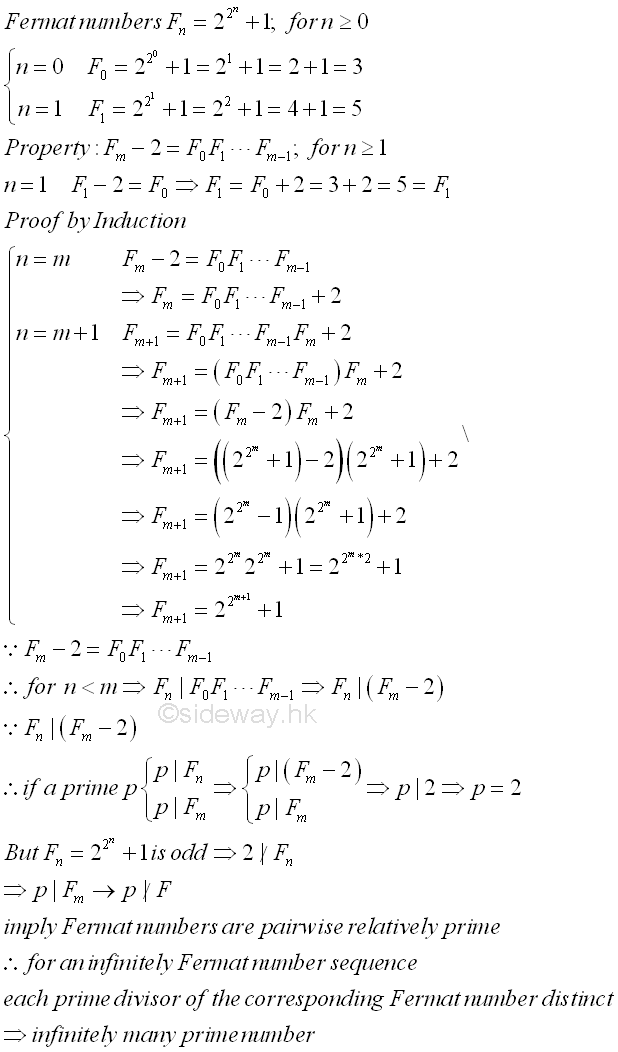

By the lemma, the property of pairwise relatively prime ensures that the sequence of prime numbers generated by choosing a prime divisor pi of each Fermat number Fi of an infinitely sequence are all distinct. Since there is at least one prime pi for each Fermat number Fi , there is at least one prime pi for every integer i. For an infinitely sequence of natural number i, there are also infinitely prime numbers. Although Fermat numbers are using in the proof, any other pairwise relatively prime sequence can also be used to prove that there are an infinitely number of primes.

Schorn's Proof[1]

Assume that there exist only finitely m prime numbers. Let n=m+1. For a pairwise relatively prime sequence with n integers of term (n!)i+1, where i=1,2,3,...,n, as shown in Goldbach's Proof, if a prime pi dividing the i term (n!)i+1, then p1, p2, p3, pi, ..., pn, are distinct primes. In the pairwise relatively prime sequence, greatest common divisor can be found by Euclid's GCD Algorithm. For any two integers i,j, if 1≤i<j≤n, then gcd((n!)i+1,(n!)j+1)=1. By expressing j = i+d where 1≤d<n, then gcd((n!)i+1,(n!)d)=1. Since every prime factor p dividing (n!)d is at most equal to n. There exist at least n prime numbers in n integers and n is greater then m, which is absurd and the infinitely sequence is confirmed.

Euler's Proof[1]

Instead of using a pairwise relatively prime sequence, Euler's proof is making use of an infinitely geometric series.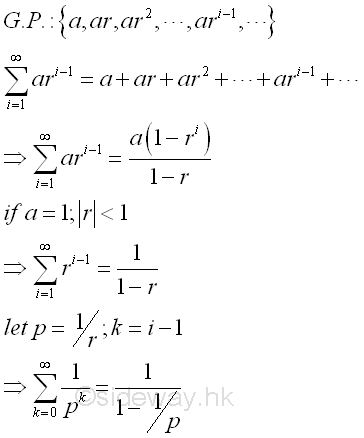

Assume that there are only finitely many prime numbers. If p is any prime number, the product of the sum of geometric series for all existing n primes is

After expanding the product of the geometric series through expanding, multiplying, and rearranging terms, the product becomes the sum of the inverses of all non-repeating natural numbers, as stated in the Fundamental Theorem of Arithmetic that every natural number is equal to the product of primes uniquely. On the right-hand side, the geometric series is divergent, the summation of the geometric series is irrelevant, and therefore the product of geometric series is infinite. However, if there are only a finite number of prime number, the product on the left-hand side is finite. This is absurd and therefore there are infinitely many prime numbers.

Thue's Proof[1]

No sequence or series is used in Thue's proof. Thue's proof is only making use of the Fundamental Theorem of Arithmetic that every natural number is equal to the product of primes uniquely. Therefore, a number m, where 1≤m≤2n can be expressed in term of primes as

Perott's Proof (1881)[1]

Assume that there are only finitely many prime numbers, p1<p2<p3<...<pk...<pm. Let N be any integer such that p1p2p3...pk...pm<N. Let j be any integers such that j≤N and is not divisible by any square of i, i.e. i2 where 1≤i≤n and 1≤j≤n.  From the Fundamental Theorem of Arithmetic, each integer j, 1≤j≤N can be expressed as p1e1, p2e2, p3e3, ..., pkek, ..., pmem, and em≥0. Therefore the ek of all pkek  greater than 1 is divisible by any i2. The number of integers j is therefore equal to 2m. By direct division, the number of integer j divisible by pk2 is equal to N/pk2  at most, the total number of integers j dividible by square of all existing prime numbers, is at most Σ m
k=1 (N/pk2). Therefore the total number of integer j can be expressed in term of all existing prime numbers.  Imply

Therefore the total number N of all nature numbers is bounded by the sum of all possible integers j. And there are infinitely many prime numbers can be prooved by choosing an sufficient large natural number N to break the bounding sum. Imply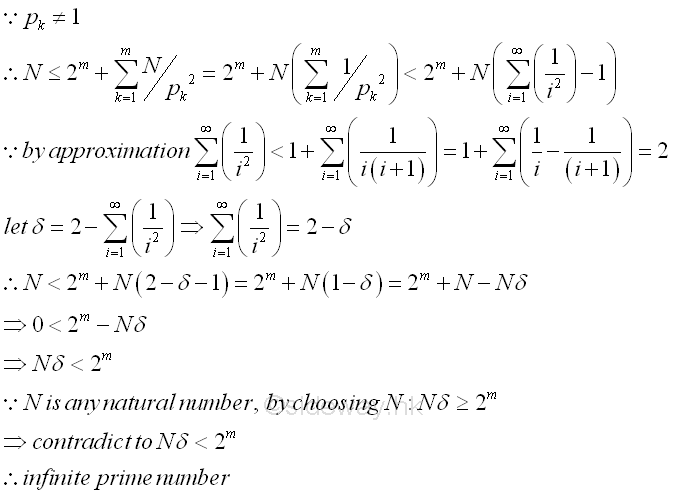

Auric's Proof (1915)[1]

Assume that there are only finitely many prime numbers, p1<p2<p3<...<pk...<pm. Let q be any integer greater or equal to 1 and an integer N=pmq. From the Fundamental Theorem of Arithmetic, each integer j, 1≤j≤N can be expressed as p1e1, p2e2, p3e3, ..., pkek, ..., pmem, and ek≥0. Therefore their relationship can be expressed as p1e1≤m≤N=pmt . Taking log and let E=(log Pr)/(log P1), imply  e1≤tE and the power of each prime number is bounded by tE. Therefore the number of integer m is equal to N and is at most the number of integer form by all finitely prime numbers. Imply, pmq=N≤(tE+1)m≤tm(E+1)m . Similarly, if t is sufficiently large, the inequality cannot hold. Therefore there are infinitely many prime numbers,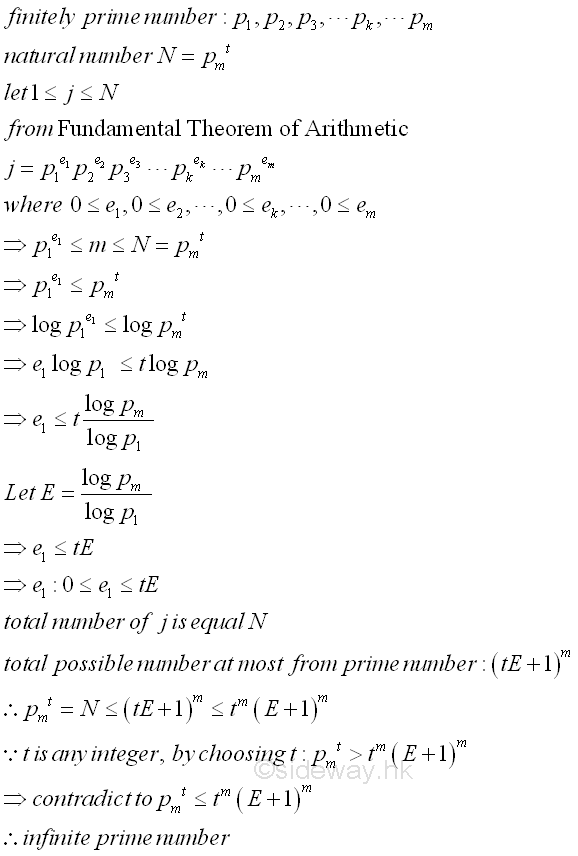

Metrod's Proof (1917)[1]

Assume that there are only finitely many prime numbers, p1<p2<p3<...<pk...<pm. Let N be equal to p1p2p3...pk...pm. Let 1≤j≤m where j≠k. Let Qk=N/pk imply pk does not Qk and pk does divide Qj for all j not equal to k. Let S=Σ m
k=1 (Qk). Therefore pk does not divide S because pk does not divide both  Qk and Qj. Thus there exists another prime S if S is already a prime or a prime p dividing S if S is a composite. More prime numbers can be generated similarly. imply there are infinitely many prime number.