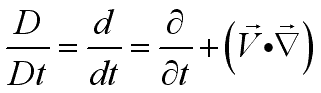Sideway
BICK BLOG from Sideway
Sideway
BICK BLOG from Sideway
|
Link:http://output.to/sideway/default.asp?qno=100100002 Fluid Kinematics Fluid KinematicsKinematics is the study of the velocity and acceleration of the fluid motion.
There are two methods to study the motion of fluid. One way can focus on fluid particles
by tracking their position vector, i.e.
Velocity FieldFluid property can be represented as a function of spatial coordinates in term of a field representation. For a fluid flow, it is also a function of time. 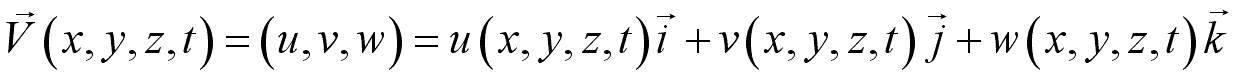
When the velocity value of a location equals to zero, Acceleration FieldIn a fluid flow, the velocity of a particle is a function of
its location and time. Imply
imply
Since the equation can be used to describe any particle, the
acceleration field can be obtained from the velocity field as And the total acceleration can be expressed as
Since the total derivative operator
The total acceleration is therefore also called material acceleration. |
Sideway BICK Blog 22/01 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
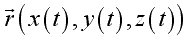 and
determining their associated properties as a function of time, i.e. velocity
vector
and
determining their associated properties as a function of time, i.e. velocity
vector
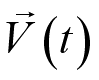 .
This is the Lagrangian description of fluid motion. The other way of describing
fluid motion is the Eulerian description of fluid motion, which focuses on the
fluid flows in and out of a control volume in terms of field variables. Instead
of following individual fluid particles, the description describes the variables
value of the location only and does not care whichever fluid particle
occupying that location inside the control volume as a function of space and
time, i.e. pressure field
.
This is the Lagrangian description of fluid motion. The other way of describing
fluid motion is the Eulerian description of fluid motion, which focuses on the
fluid flows in and out of a control volume in terms of field variables. Instead
of following individual fluid particles, the description describes the variables
value of the location only and does not care whichever fluid particle
occupying that location inside the control volume as a function of space and
time, i.e. pressure field
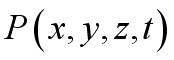 , velocity field
, velocity field
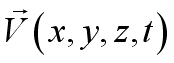 to define the flow field.
to define the flow field.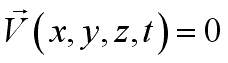 i.e.
i.e.
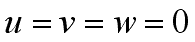 ,
it is called a stagnation point.
,
it is called a stagnation point.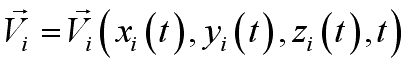 .
By definition, the acceleration of a particle is the time rate of change of its
velocity,
.
By definition, the acceleration of a particle is the time rate of change of its
velocity,
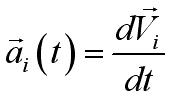 . Using chain rule of differentiation,
. Using chain rule of differentiation,
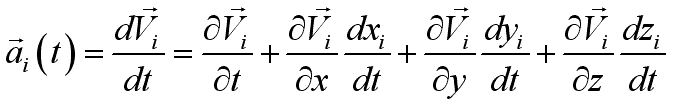 and because
and because
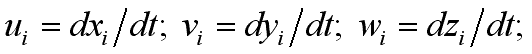
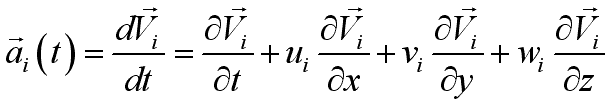 .
.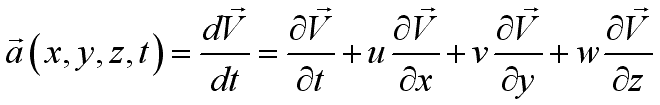 ,or
,or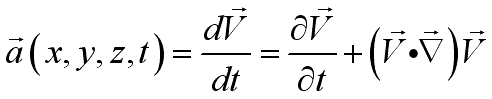 ;
;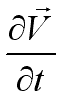 is named local acceleration or unsteady acceleration, which equals to zero for
steady flow and
is named local acceleration or unsteady acceleration, which equals to zero for
steady flow and
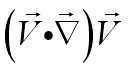 is named advective acceleration or convective acceleration, which equals to
non-zero even for steady flow.
is named advective acceleration or convective acceleration, which equals to
non-zero even for steady flow.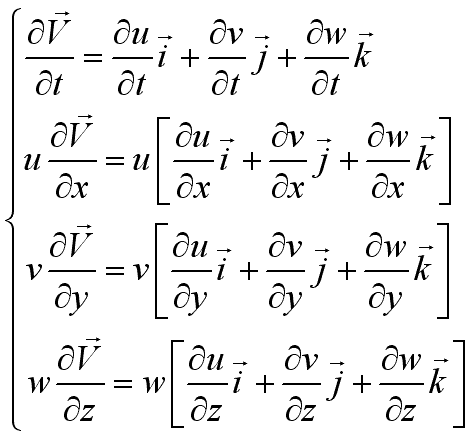 or
or
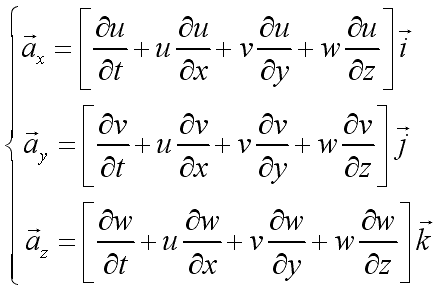
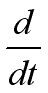 is derived from a fluid particle, it is called material derivative,
is derived from a fluid particle, it is called material derivative,
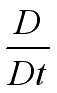 .
i.e.
.
i.e.