 Sideway
BICK BLOG from Sideway
Sideway
BICK BLOG from Sideway
|
Link:http://output.to/sideway/default.asp?qno=101000022 Sound in Enclosure 3D Wave Reflection inside Enclosures, 3DThe 3D wave equation is 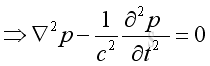
Assume harmonic sound wave imply 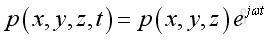
Take the time differential operation, imply 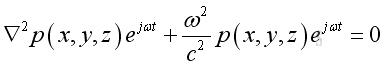
And get the Helmoltz equation, 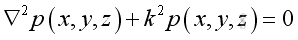
Assume the pressure is of format: 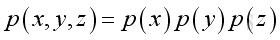
substitute the pressure function into the helmoltz equation, and take the Laplacian differential operation: 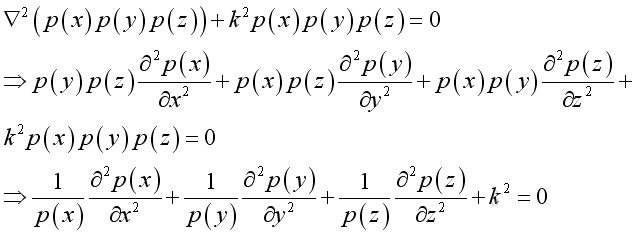
let the dispersion equation : 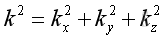
substitute into the Helmoltz equation: 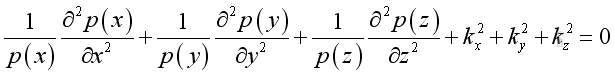
By separating the variable, imply: 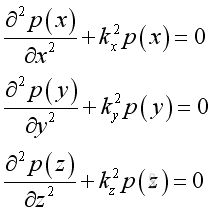
Assume the corresponding solution of the equation of the form,
Assume the rectangular enclosure are with rigid walls, the boundary conditions at 6 walls are with particle velocity equals to zero, imply
and
From the equation of momentum conservation in x direction 
At x = 0 or x=Lx, u=0 at all time, therefore the time derivative of u is zero also, imply:
Therefore at x=0 and x=Lx, imply : 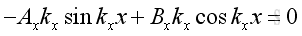
From boundary condition at x=0, imply: 
From boundary condition at x=Lx, imply: 
Substitute kx, A and B into the pressure function, imply:
Similarly ky, kz,are:
And the corresponding pressure function in y and z direction are:
Substitute all individual pressure functions into the total pressure function is:
Substitute all individual wave number into the combined wave number is:
Therefore the frequency is :
Number of ModesThe number of modes increases dramatically with the increase of frequency and with the volume of the cavity and can be estimated by. 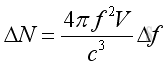
Link:http://output.to/sideway/default.asp?qno=101000021 Sound in Enclosure Wave Reflection inside Enclosures, 1DA sound source radiates outwardly in any direction in a free source will always encounter reflecting surfaces unless the sound source is place in an anechoic chamber where all sound energy is almost absorbed with any reflection. And in such case then only wave equation should be satisified without any boundary conditions. Multiple reflection in an enclosure due to the wall creates standing waves with acoustic modes charactered by frequencies and mode shapes. These modes should satisfied the wave equation and boundary conditions simultaneously. The boundary conditions are usually defined in terms of continuity between the wall motion and the particle velocity. 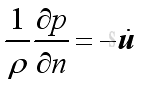
The wall characteristics are usually expressed in term of impedance. A rigid wall is used to describe a wall with higher impedance while a soft wall is used to describe a wall with lower impedance. 
Duct, 1D mode, with two closed ends
The 1D wave equation is 
Assume harmonic sound wave imply 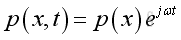
Take the time differential operation, imply 
And get the Helmoltz equation, 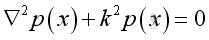
Assume the solution of the equation of the form, 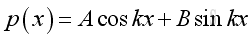
Assume the two closed ends are rigid wall, the boundary conditions at two ends are with particle velocity equals to zero, imply
From the equation of momentum conservation 
At x = 0 or x=L, u=0, therefore the time derivative of u is zero also, imply: 
From boundary condition at x=0, imply: 
From boundary condition at x=L, imply: 
Substitute k, A and B into the pressure function, imply:
Therefore the natural frequency and mode shape is:
Duct, 1D mode, with two open ends
The 1D wave equation is 
Assume harmonic sound wave imply 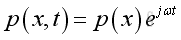
Take the time differential operation, imply 
And get the Helmoltz equation, 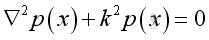
Assume the solution of the equation of the form, 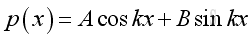
With two open ends, the boundary conditions at two ends are with pressure equals to zero, imply
From boundary condition at x=0, imply: 
From boundary condition at x=L, imply: 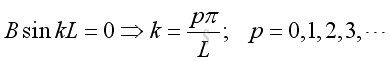
Substitute k, A and B into the pressure function, and p<>0, imply:
Therefore the natural frequency and mode shape is:
Duct, 1D mode, with one end open and one end closed
The 1D wave equaton is 
Assume harmonic sound wave imply 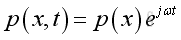
Take the time differential operation, imply 
And get the Helmoltz equation, 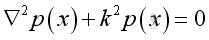
Assume the solution of the equation of the form, 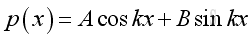
Assume the closed end is rigid wall, the boundary conditions at closed end is with particle velocity equals to zero, imply 
From the equation of momentum conservation 
At x = 0, u=0, therefore the time derivative of u is zero also, imply: o, imply: 
From boundary condition at x=0, imply: 
From boundary condition at x=L, imply: 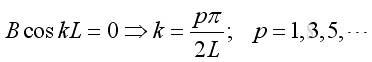
Substitute k, A and B into the pressure function, imply:
Therefore the natural frequency and mode shape is:
|
Sideway BICK Blog 20/10 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
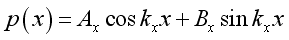
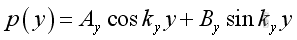
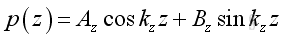
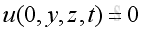 ,
,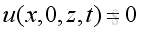 ,
,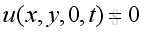
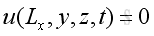 ,
,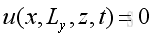 ,
,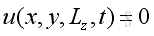
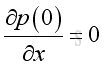 and
and
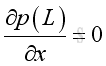
 and
and
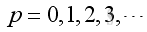
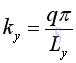 and
and
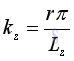
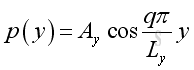 and
and
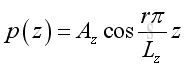 , where
, where
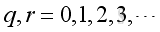
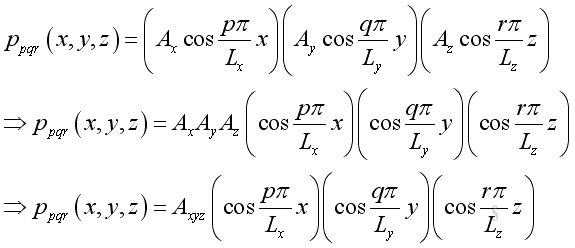 where
where
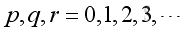
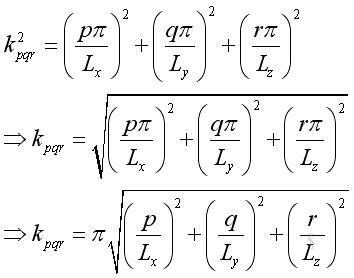 where
where
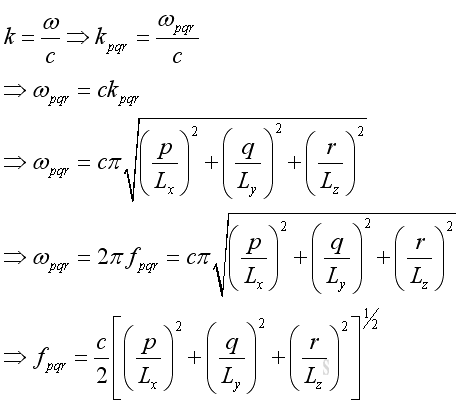 where
where

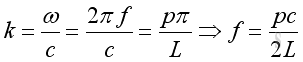 ,
,
 and
and
 and
and

 and
and
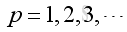
 and
and
 and
and

 ,
,
 and
and

