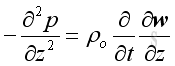Sideway
BICK BLOG from Sideway
Sideway
BICK BLOG from Sideway
|
Link:http://output.to/sideway/default.asp?qno=101000015 Acoustic Spherical Wave Acoustic Spherical WaveWhen a small spherical sound source propagates outward uniformly and radically in a free space. The acoustic functions are spherically symmetric and therefore are functions of time and radial coordinate only. Acoustic Spherical Wave EquationSince there is no tangential motion during wave propagation, the spatial operator on the pressure in the wave equation can be converted to 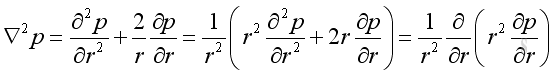
substitute the spherical operator into the rectangular wave equation: 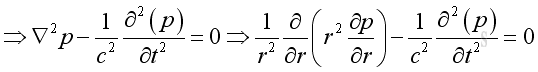
Therefore the 3D wave equation in spherical coordinate system is:
Acoustic Spherical WaveThe general solution of the spherical wave is: 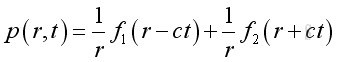
for harmonic wave, it can be expressed as 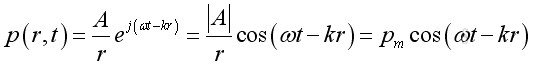
or 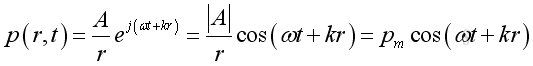
The acoustic pressure of a spherical wave is inversely proportional to the distance from the source. Therefore when the distance r is doubled, the pressure will be reduced by 6dB. Since there is no tangential motion in spherically symmetric wave, a linearized relationship with spherical coordinates between radial velocity and radial pressure from the momentum conservation can be obtained: 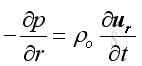
Assume the radial velocity of the form 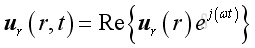
The time derivative of the velocity is: 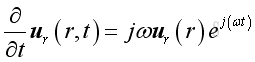
Substitute all variables into the momentum conservation equation and get the radial velocity in term of its acoustic pressure : 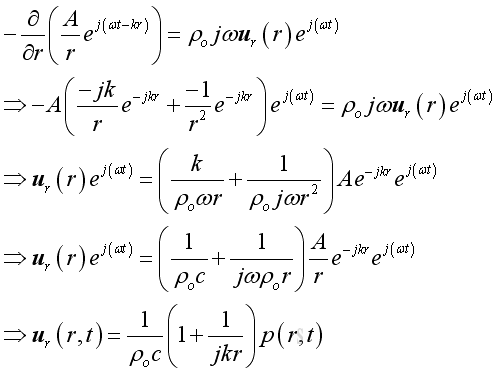
Substitute acoustic pressure into the acoustic velocity imply the real part of acoustic velocity : 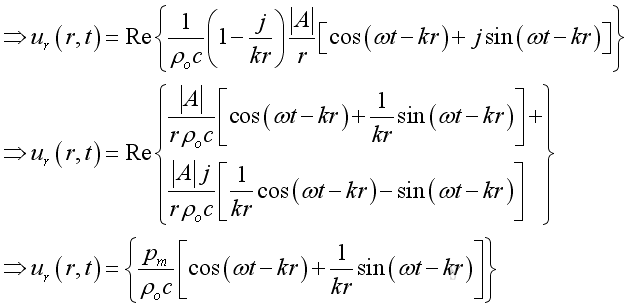
Therefore the modulus or absolute value is: 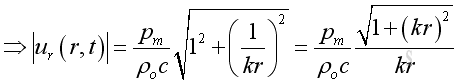
The acoustic velocity composes of two parts. The first part is in phase with the acoustic pressure with property 1/r as the propagating part. While the second part is not in phase with the acoustic pressure with property 1/r2 as the evanescent part. When the in phase component is comparable to the not in phase component, the position of interest is in the near field. Otherwise it is in the far field. The root mean square velocity is: 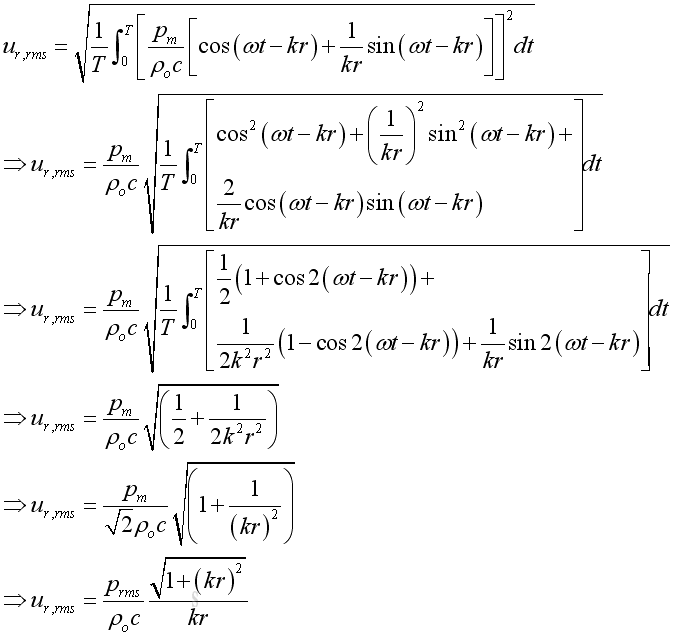
Acoustic Intensity Similar to the plane wave, the instantaneous intensity is: 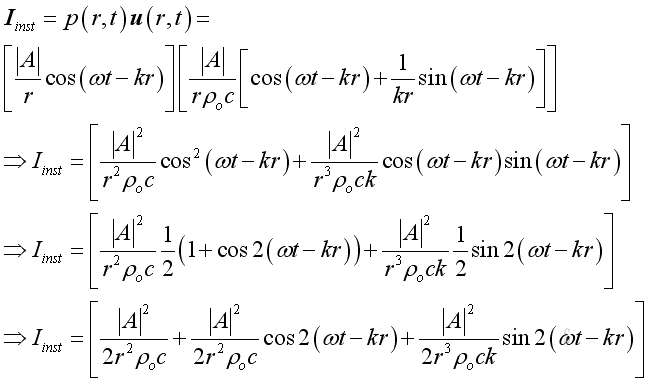
Similarly, the intensity usually expressed as an average in practice. The mean or time average intensity, in which the cosine and sine term of function of time becomes zero, imply: 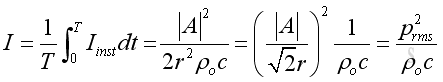
Although the expression for a spherical wave is same as that for the plane wave, the root mean square acoustic pressure is no longer a constant and is inversely proportion to the distance r from the source. Besides, only the propagating component contributes the intensity. The evanescent component is not in phase with the pressure becomes zero after the time average process because of its oscillating property Acoustic Power The total acoustic power is the integration of intensity over the spherical area enclosing the enclosure and equals 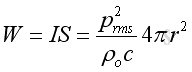
The total acoustic power is a constant and independent of distance r. Since the acoustic pressure is inversely proportion to r and the spherical surface area is proportion to r2. As intensity is proportion to square acoustic pressure, the distance r will be cancelled. Link:http://output.to/sideway/default.asp?qno=101000014 Acoustic 3D Plane Wave Acoustic 3D Plane WaveThe 1D plane wave can be extended into a 3D plane wave by considering a rectangular volume with coordinates x, y, z. Continuity Equation, 3DFor a control volume, from the principle of conservation of mass, the instantaneous rate of change of mass in a control volume equals to the net mass flux flow into or out of the control volume, therefore: 
As in 1D plane wave, the linearized form is :
And the time derivative of the equation is: 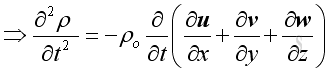
Euler's Equation of Inviscid Motion, 3DFor a control volume, from principle of momentum conservation, the instantaneous rate of change of net momentum of a control volume equals to the net applied force and the net momentum change due to the momentum flux flow into or out of the control volume. The applied force in this case is pressure only and no other forces, no gravity, no viscous force etc., then: In x direction: 
As in 1D plane wave, the linearized form is :
And the position derivative of the equation is 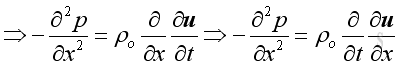
Similarly in y and z direction is
And get:: 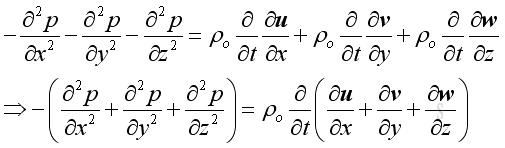
Equate two equations:: 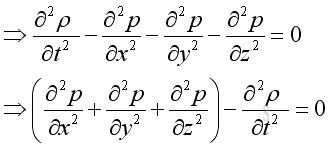
Wave Equation, 3D Applying the equation of state and substitute the speed of propagation, imply. 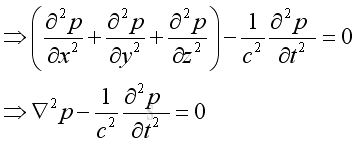
Plane Wave in 3D Assume harmonic sound wave, imply 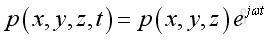
substitute the harmonic function into the 3D wave equation and take the time differential operation, imply: 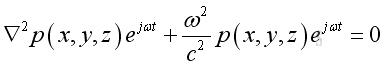
and get the Helmholtz equation: 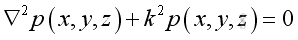
Assume the pressure is of format: 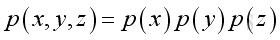
substitute the pressure function into the Helmholtz equation, and take the Laplacian differential operation: 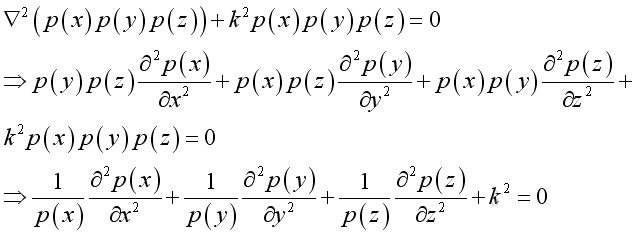
let the dispersion equation : 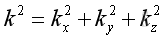
substitute into the Helmholtz equation: 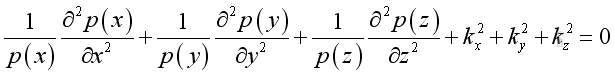
By separating the variable, imply: 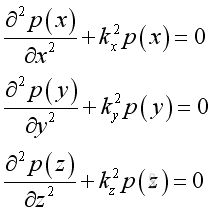
The corresponding solutions are: 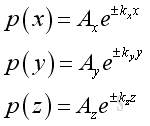
substute all into the pressure function and get the solution of wave equation is: 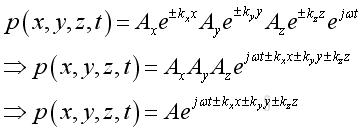
Therefore a propagating wave can be decomposed into three components along three axes. A positive sign implies a forward wave from the source to the free space. While a negative sign implies a reflected wave. With the dispersion of the value, k into three components along the three axes |
Sideway BICK Blog 16/10 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
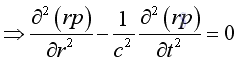
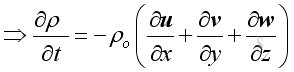
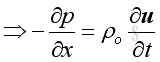
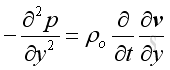 and
and