 Sideway
BICK BLOG from Sideway
Sideway
BICK BLOG from Sideway
|
Link:http://output.to/sideway/default.asp?qno=110600003 Moment about axis Moment of force about axisThe moment of a force about a reference point is represents by a moment vector, MO normal to the plane formed by the reference point and the line of action of the force. The direction of moment vector also specifies the axis of rotation. Therefore when the rotating axis, OL is specified, the moment of a force is also limited to rotate about the specified rotating axis only. 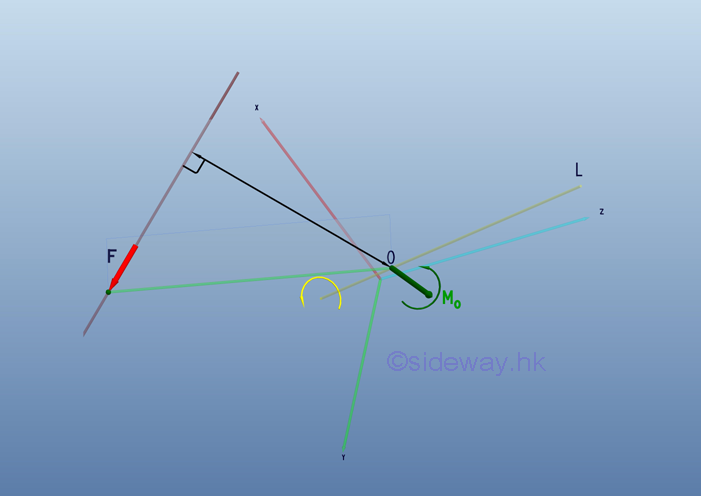
Force Decomposition Physically, the effective moment MOL about a specified axis is only due to the force lying on the plane normal to the specied axis and the moment due to the force parallel to the specified axis is zero. Besides, the effective moment MOL and the moment MO also form a rotating angle in the space. 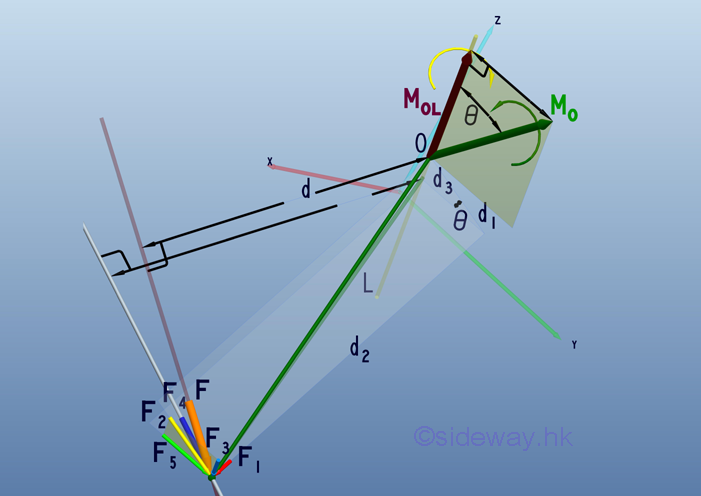
Geometrically, a plane can be constructed by the moment MO of force F about a point O and the axis OL. Therefore force (orange) F can be resolved into force (red) F1 normal to the plane and force (yellow) F2 parallel to the plane. Imply the moment of force F about a point O equals: 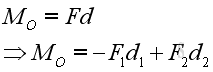
In order to determine the effective moment MOL of the applied force F about the specified axis OL, the applied force F is resolved into two retangular components with one force (cyan) F3 parallel to the specified axis and the other force (blue) F4 lying on the normal plane of the specified axis. Force F4 can further be decomposed into two retangular components with one force equals to the force (red) F1 and the other force (green) F5 lying on the normal plane of the force (red) F1 . Since the force (cyan) F3 is parallel to the specified axis, the moment of the force about the specified axis is equal to zero, Imply the moment of force F about a specificed axis OL equals: 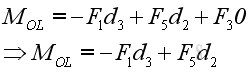
Through force decomposition, force F is resolved into three retangular components, F1, F3, and F5. And Force F2 can also be resolved into two retangular components, F3, and F5. According to the geormetry, force F5 can be expressed as 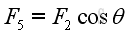
Besides, the moment arm d3, can also be expressed as: 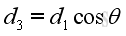
Substitute all variables, and the effective moment MOL equals: 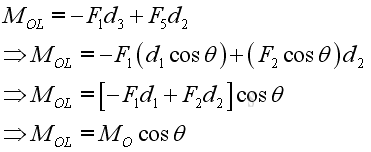
Moment Decomposition The effective moment about a specified axis can be determined by moment decomposition. The moment, MO can be resolved into two retangular components with the moment, MOL along the specified axis and the other moment normal to the specified axis on a plane formed by the two axes. Therefore the effective moment, MOL about a specified axis is equal to the moment, , MO projected on the axis, OL. 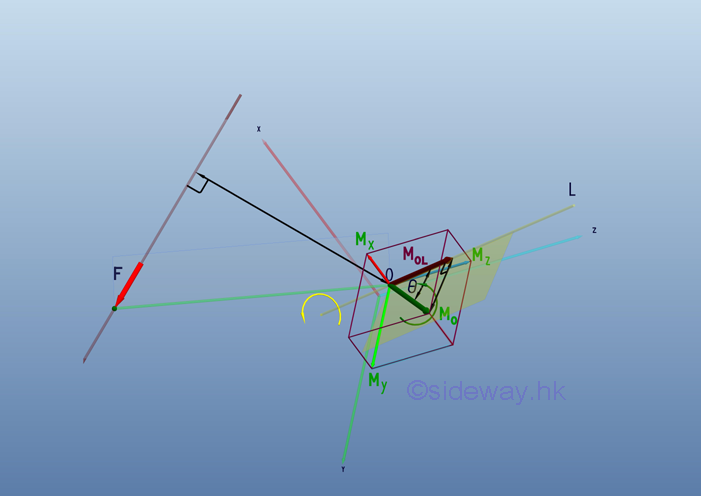
The magnitude of moment vector, MOL can be expressed as: 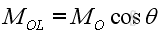
The moment vector, MO in the form of three retangular components is 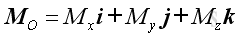
Let the unit vectors of moments, MO and MOL are λO and λOL and they can be expressed as:
where:
From the law of cosine, imply 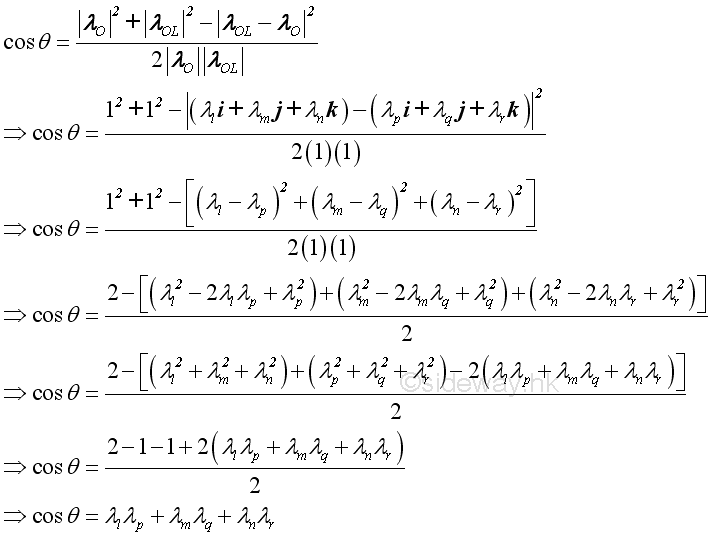
Therefore the moment about the specified axis can be expressed as: 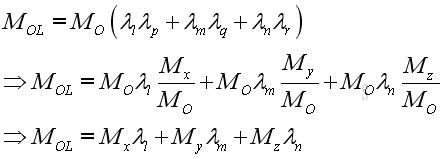
Moment Vector The magnitude of moment MOL of a force F about a specified axis OL can be defined as the scalar product of the unit vector λOL along the axis OL and MO. 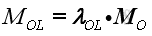
Imply 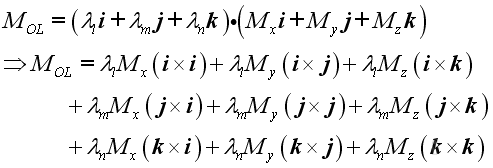
Since the scalar product of two vectors is the product of the magnitudes of the two vectors and the cosine of the angle formed by the vectors, imply 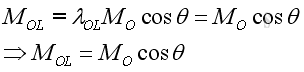
Therefore, the scale product of a unit vector with itselt is equal to one, imply
And, the scale product of two different unit vectors is equal to zero, imply
Substitute all variables into the moment vector equation, imply
Since the moment of force about a point can be expressed as the vector product of the position vector and the force vector, imply the magnitude of the moment of force about a fixed axis equals to the mixed triple product of three vectors
Imply :
The magnitude of the moment of force about a fixed axis can also be expressed in the determinant form, :
|
Sideway BICK Blog 19/06 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
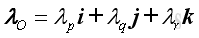 and
and
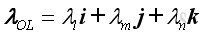
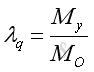 ,
,
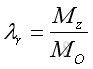
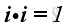 ,
,
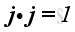 and
and
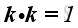
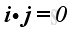 ,
,
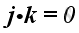 and
and
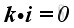
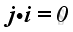 ,
,
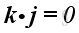 and
and
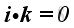
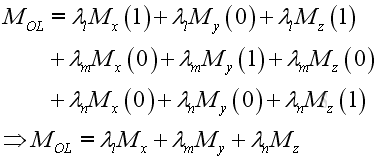 .
.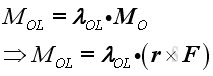 .
.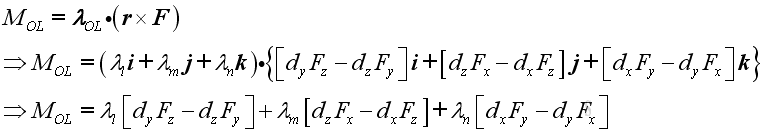 .
.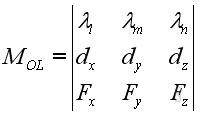 .
.
