 Sideway
BICK BLOG from Sideway
Sideway
BICK BLOG from Sideway
|
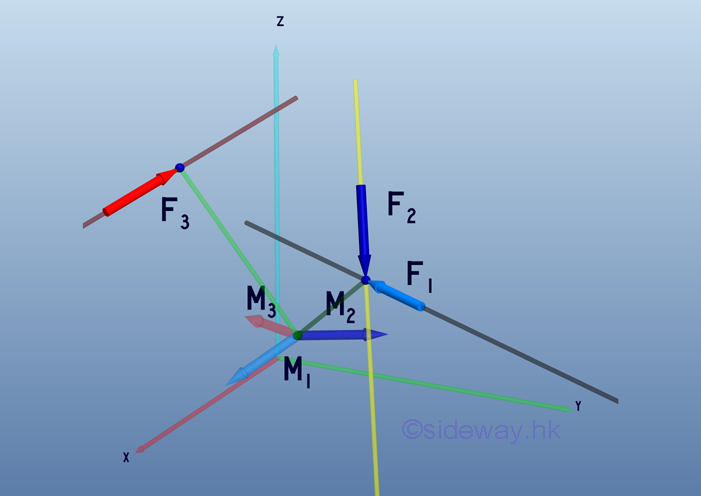
Link:http://output.to/sideway/default.asp?qno=110600002 Moment in 3D Moment of force in 3D about a pointWhen an application is subjected to forces in space, the determination of the effective moment of forces about a reference point is much more complicated than application with forces in a plane. In most case, the effective moment in space can only be determined by moment vectors addition in space instead of algebraic addition of moment vectors in the 2D case.
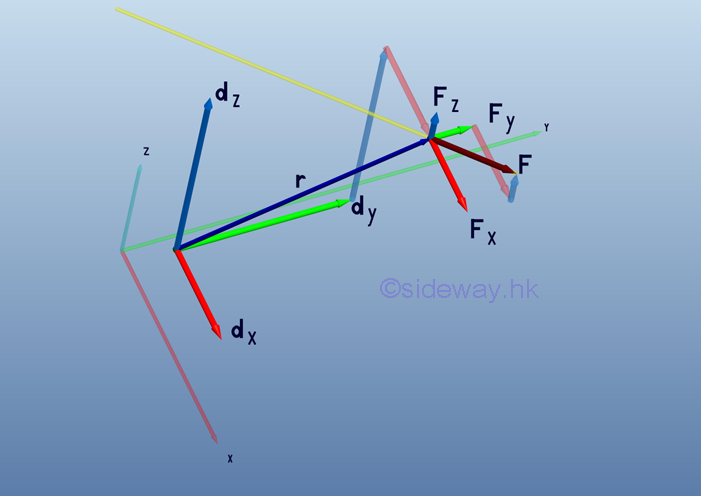
Moment Decomposition Since the effective moment of concurrent forces about a reference point is equal to the sum of the moments of the concurrent forces as stated in Varignon's Theorem. Both the force vector and the position vector can be resolved into three rectangular components as in the 2D case. A force vector, F in space can be resolved into three retangular components, Fx Fy and Fz. The position vector, r in space can also resolved into three retangular components, dx, dy and dz. Similarly, the moment vector, M of force, F can also be resolved into three retangular components, Mx, My and Mz.
Therefore, the force vector, F and position vector, r can be expressed as:
And express the resultant moment vector, M in the form of three retangular components 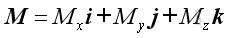
The moment M of a force F about a reference point can be defined as the vector product of r and F. 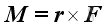
Imply. 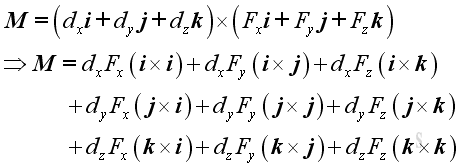
Since the magnitude of vector product is the product of the magnitudes of the two vectors and the sine of the angle formed by the vectors, imply 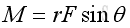
Therefore, the vector product of a unit vector with itselt is equal to a zero vector, imply
For the sense of the direction, the vector product of two different unit vectors is equal to the unit vector in the third dimension according to the right hand rule, imply
Substitute all variables into the moment vector equation, imply
Each force component exerts zero moment along its own dimension, and exerts two moments with opposite sense along the other two dimensions. By grouping moments along the same dimension, moment, M can therefore be decomposed into three retangular components:
The magnitude of the three retangular components can be determined by:
The sense or direction of the moment is indicated by the sign of the retangular resultant component. The moment can be expressed in the determinant form:
Moment Addition The effective moment of forces about a reference point in space can be represented by a moment vector, M, in three dimensional space.
The most practical way of determining the resultant moment in space is to add up their rectangular components respectively.
where:
|
Sideway BICK Blog 13/06 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
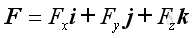 and
and
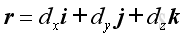
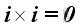 ,
,
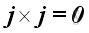 and
and
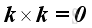
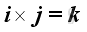 ,
,
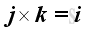 and
and
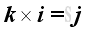
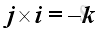 ,
,
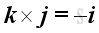 and
and
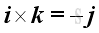
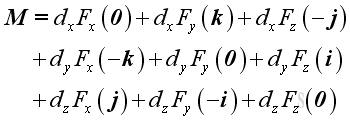 .
.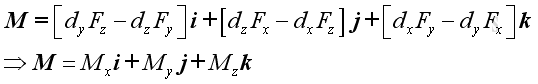 .
.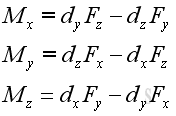 .
.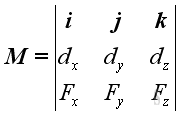 .
.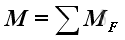 .
.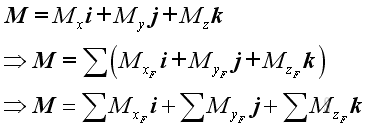 .
.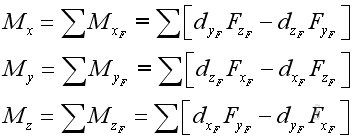 .
.
