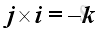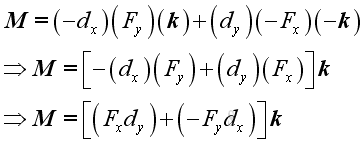Sideway
BICK BLOG from Sideway
Sideway
BICK BLOG from Sideway
|
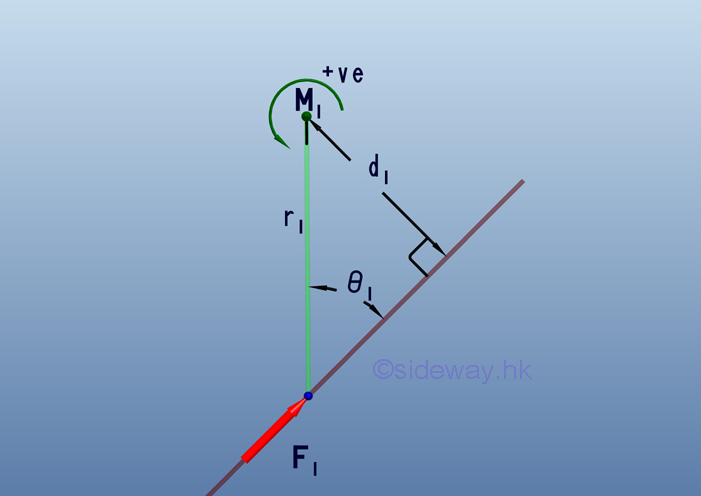
Link:http://output.to/sideway/default.asp?qno=110600001 Moment in 2D Moment of a force in 2D about a pointWhen an application is subjected to coplanar forces, forces in a plane and the effect of the depth on structure analysis is negligible, the problem can be simplified into two dimensional analysis. Because the direction of moment of a force is always normal to the plane joining the reference point and the line of action, the moment of forces in a plane about a point can therefore refer to the sense of the moment about a point.
According to the right hand rule, a counterclockwise moment about a reference point can be taken as positive, while a clockwise moment about a reference point can be taken as negative.
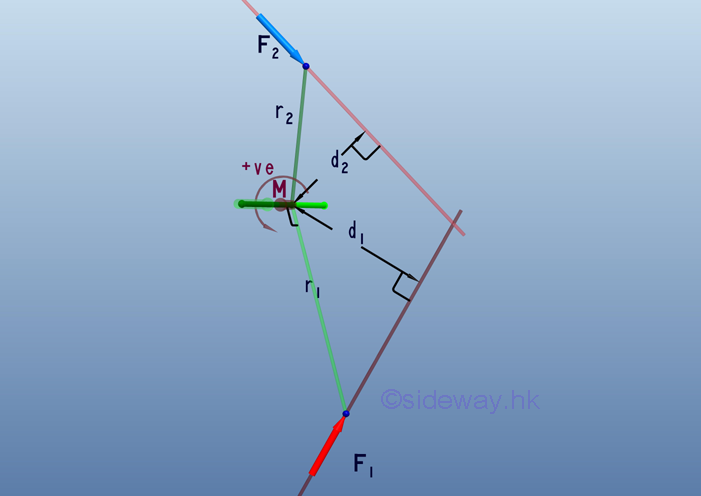
Moment Addition of Coplanar Forces The total moment of forces about a reference point can be determined by adding up all moments of forces.
Therefore, the magnitude of the effective moment , M, can be expressed as:
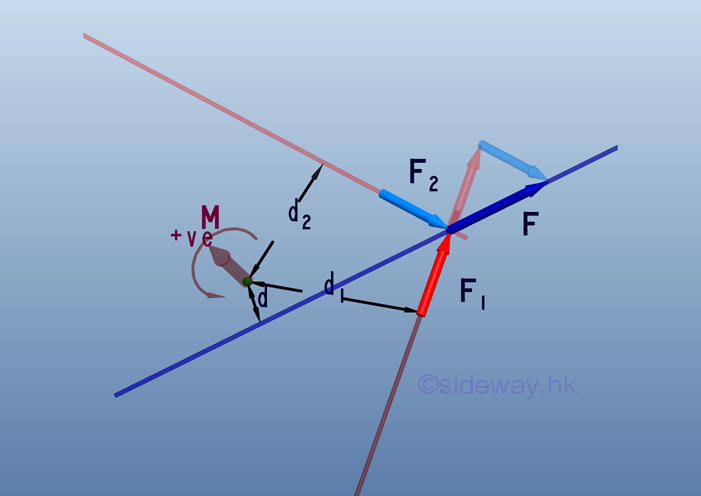
Moment of Concurrent Forces For concurrent forces, the moment of the resultant of concurrent forces is also equal to the resultant force times the prependicular distance between the reference point and the line of action of the rusultant force. The effective moment can also be computed by adding up all individual moment of concurrent forces.
Therefore, the magnitude of the moment , M, can be expressed as:
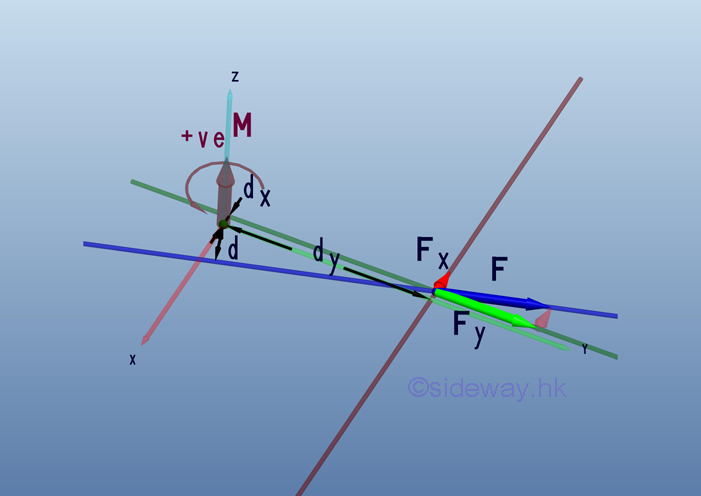
Moment Decomposition Since the effective moment of concurrent forces about a reference point is equal to the sum of the moments of the concurrent forces as stated in Varignon's Theorem. In other words, moment of a force can also be decomposed through force decomposition. A force, F in a plane can be decomposed into two retangular components, Fx and Fy. The moment, M of force, F can therefore be decomposed into MFx and MFy.
Therefore, the magnitude of the moment , M, can be expressed as:
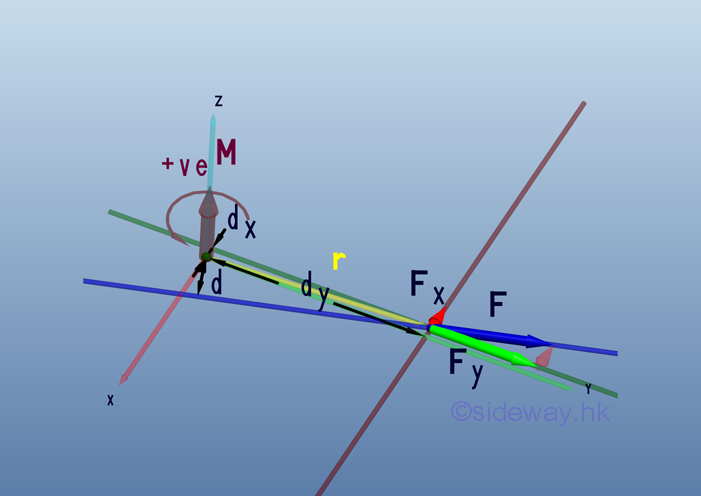
Moment Vector When the force vector is decomposed into two rectangular components, the corresponding perpendicular distance components are also equal to the magnitudes of the two rectangular components of the postition vector, r of the point of application. And the moment vector, M becomes the third dimension of the rectangular coordinate system.
Therefore the force vector, F and position vector, r can be expressed as:
where the minus sign indicates the direction as usual The moment of a force, M about a reference point can be defined as the vector product of r and F. 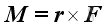
Imply
Since the magnitude of vector product is the product of the magnitudes of the two vectors and the sine of the angle formed by the vectors, imply 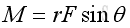
Therefore, the vector product of a unit vector with itselt is equal to a zero vector, imply
For the sense of the direction, the vector product of two different unit vectors is equal to the unit vector in the third dimension according to the right hand rule, imply
Substitute all variables into the moment vector equation, imply
|
Sideway BICK Blog 07/06 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

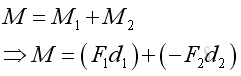
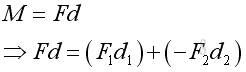
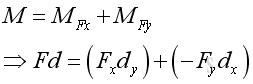
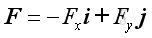 and
and
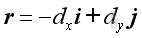
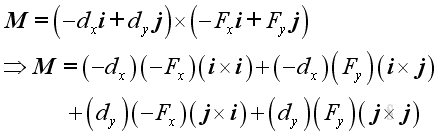
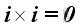 and
and
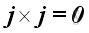
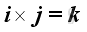 and
and