 Sideway
BICK BLOG from Sideway
Sideway
BICK BLOG from Sideway
|
Link:http://output.to/sideway/default.asp?qno=121100086 Moment of Inertia of Mass, Mass Moment inertia of Common Shapes Moment of Inertia of Common ShapeIn general, the second moment of mass in space about an axis can be determined by 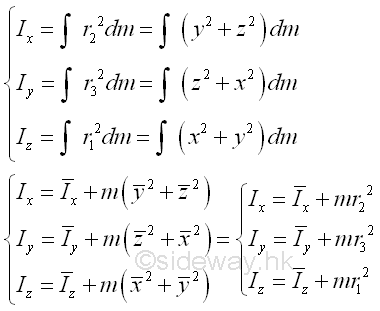
Moment of Inertia of a Mass of Homogeneous BodyMoment of Inertia of Slender Rod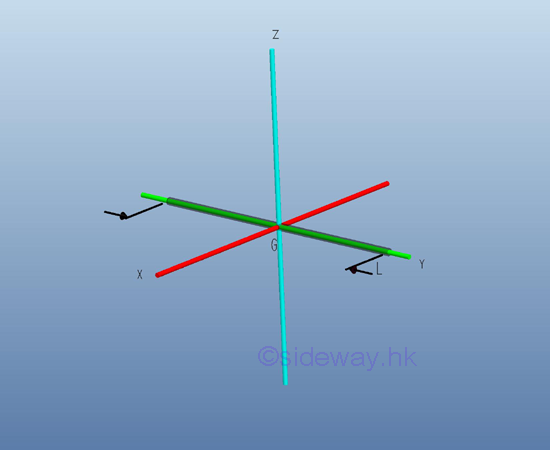
Consider a slender homogenous circular rod of length L with uniform cross-sectional area A and homogenouse material density ρ. Both the cross-sectional area and the material density are constant over the lenght. Since the cross-sectional radius r is much smaller than the length of slender rod, the mass and the elemental mass of the slender rod can be expressed in terms of the mass per unit length, if the reference axis lies in centre of gravity of the slender rod, the mass moment of inertia of the slender rod with respect to an centroidal axis can be expressed as the elemental mass on the axial axis with the distance x as the radius between the elemental mass and the reference axis. Imply 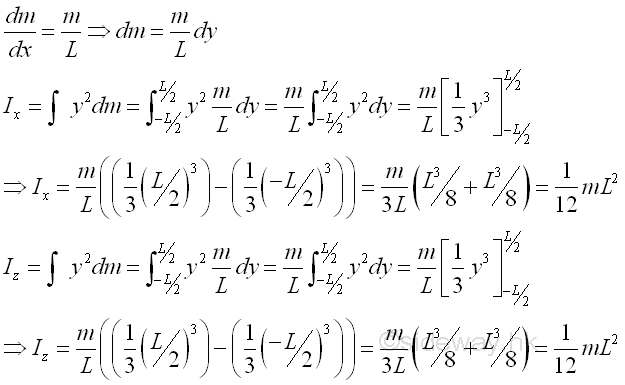
Moment of Inertia of Circular Cylinder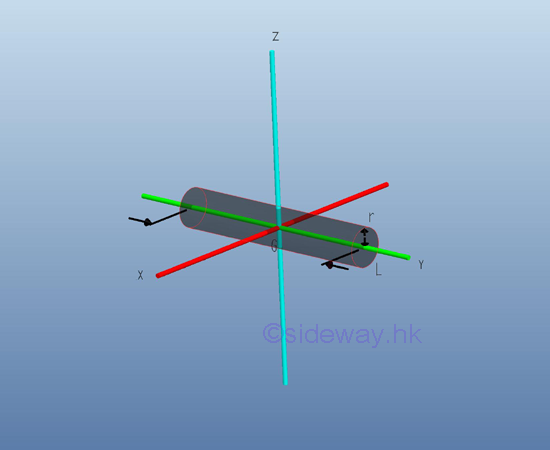
Consider a homogenous circular cylinder of length L with uniform cross-sectional area A of radius r and homogenouse material density l. Both the cross-sectional area and the material density are constant over the lenght, the mass and the elemental mass of the circular cylinder can be expressed in terms of the volume of the circular cylinder. Since the cross-sectional radius r cannot be neglected, the actual distance between the elemental mass and the reference axis should be used. The moments of inertia about axes x and z, can be determined by parallel-axis theorem. Imply 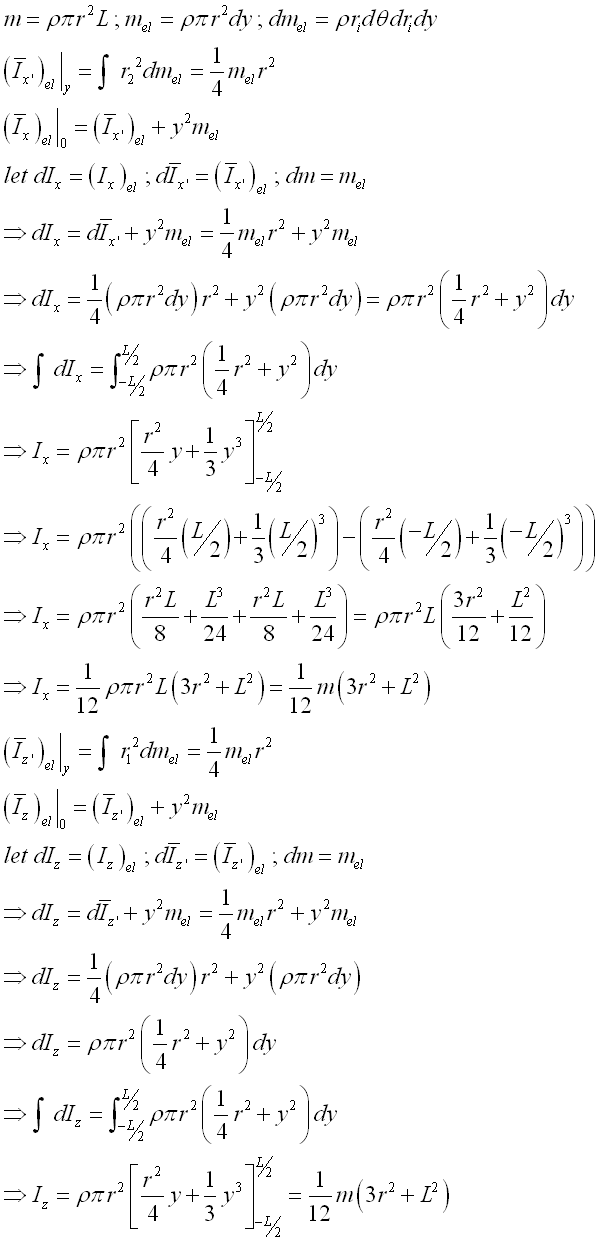
And the moments of inertia about axis y can also be determined by parallel-axis theorem. Imply 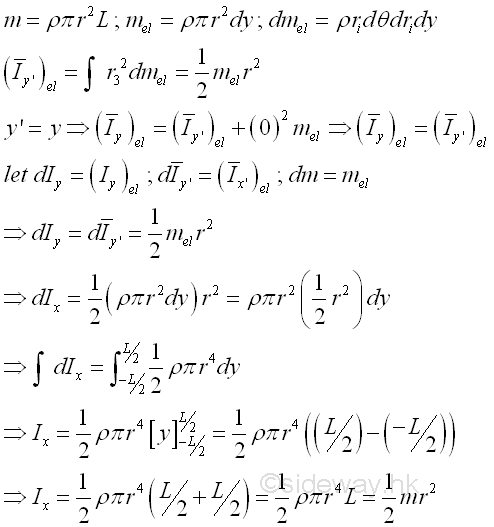
Moment of Inertia of Rectangular Prism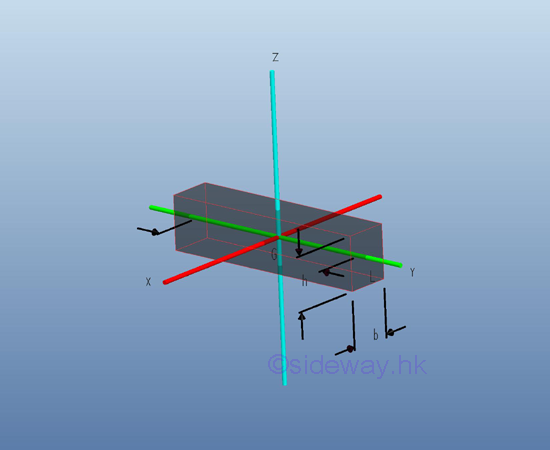
Consider a homogenous rectangular prism of length L with uniform cross-sectional area A of height h, width b and homogenouse material density l. Both the cross-sectional area and the material density are constant over the lenght, the mass and the elemental mass of the rectangular prism can be expressed in terms of the volume of the rectangular prism. Since the cross-sectional dimensions cannot be neglected, the actual distance between the elemental mass and the reference axis should be used. The moments of inertia about axes x and z, can be determined by parallel-axis theorem. Imply 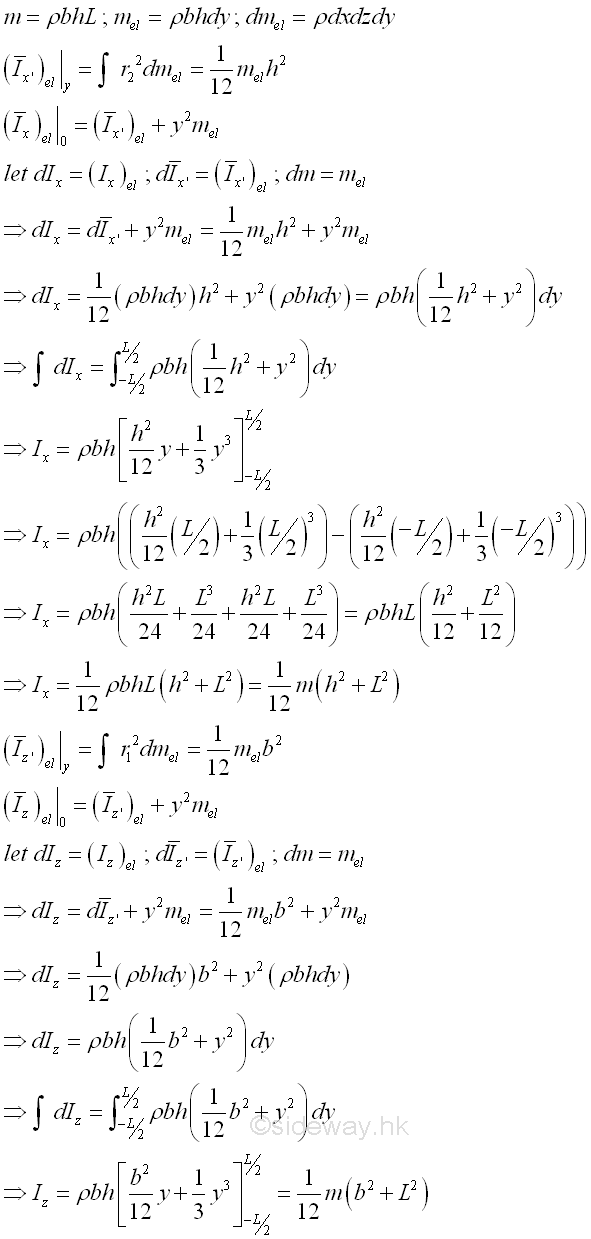
And the moments of inertia about axis y can also be determined by parallel-axis theorem. Imply 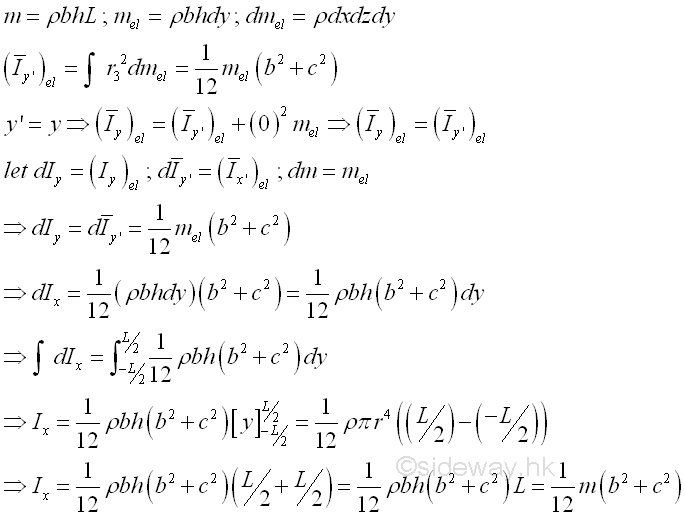
Moment of Inertia of Circular Cone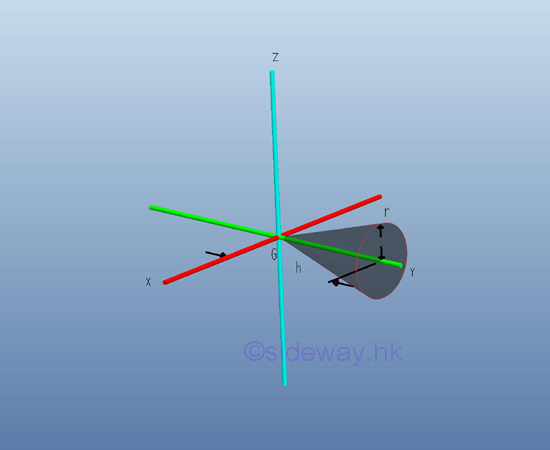
Consider a homogenous circular cone of height h with base area A of radius r and homogenouse material density l. The material density is a constant, the mass and the elemental mass of the circular cone can be expressed in terms of the volume of the circular cone. Since the radius r of the base area cannot be neglected, the actual distance between the elemental mass and the reference axis should be used. The moments of inertia about axes x and z, can be determined by parallel-axis theorem. Imply 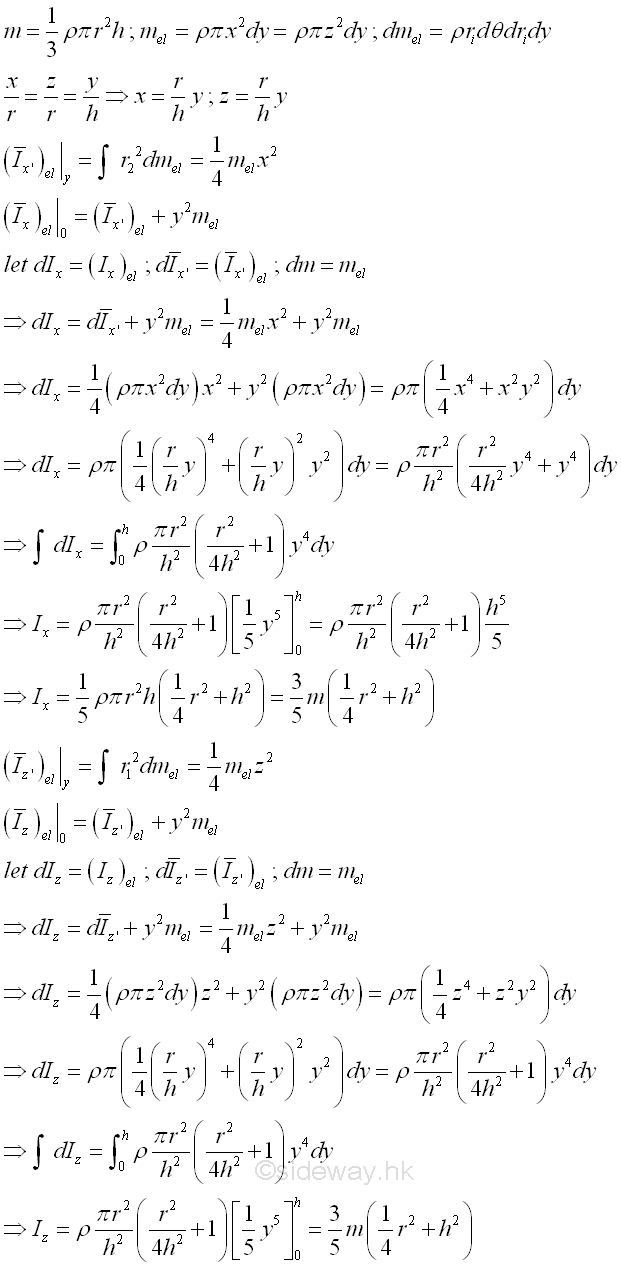
And the moments of inertia about axis y can also be determined by parallel-axis theorem. Imply 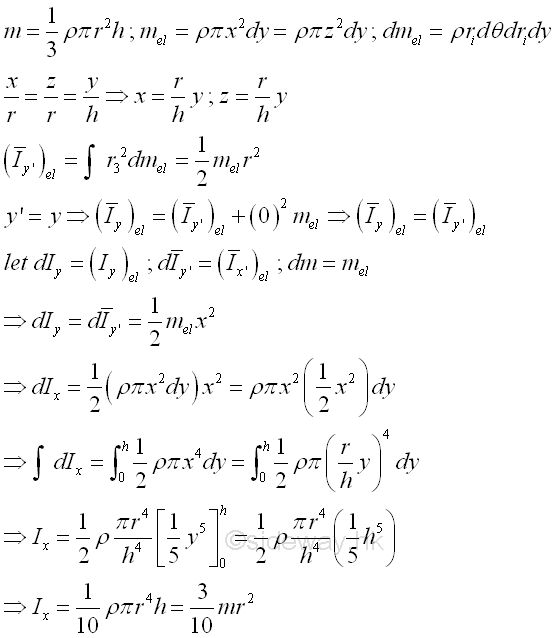
Moment of Inertia of Sphere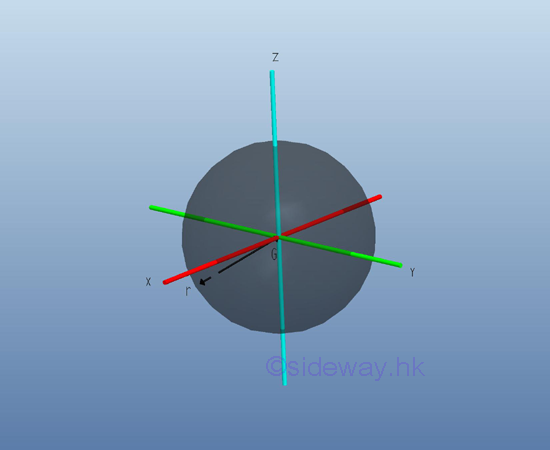
Consider a homogenous sphere of radius r and homogenouse material density l. The material density is a constant, the mass and the elemental mass of the circular cone can be expressed in terms of the volume of the circular cone. Since the radius r of the sphere area cannot be neglected, the actual distance between the elemental mass and the reference axis should be used. The moments of inertia about axes x, y and z, can be determined by triple integration. Imply 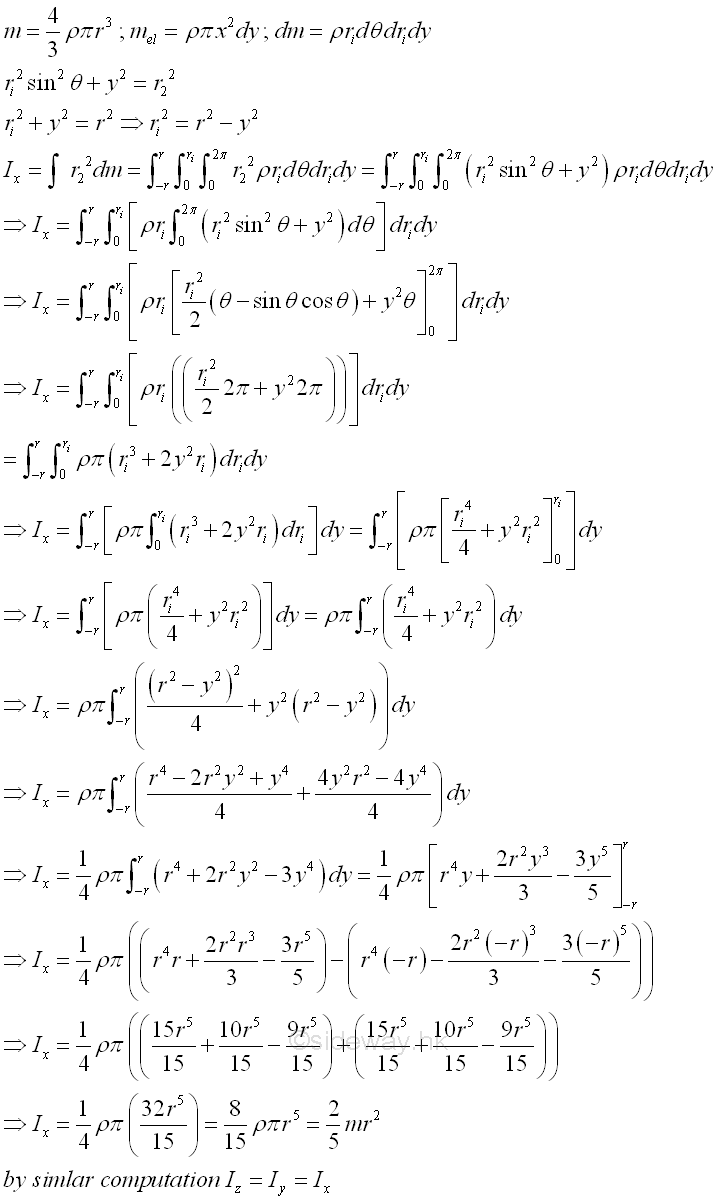
|
Sideway BICK Blog 14/11 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

