 Sideway
BICK BLOG from Sideway
Sideway
BICK BLOG from Sideway
|
Link:http://output.to/sideway/default.asp?qno=121100087 Moment of Inertia of Mass, Mass Moment inertia of Composite Body Moment of Inertia of Composite BodyBy definition, moment of inertia about an axis is equal to the summation of the products of the square of the distance between the elemental mass and the reference axis, and the elemental mass over the body. If these elemental mass can be grouped into known component masses M1, M2, M3, ...., the second moment I of the composite body A with respect to an axis can be obtained by the summation of the second moments, I1, I2, I3, .... of these component masses M1, M2, M3, ...., about the same reference axis respectively. Imply 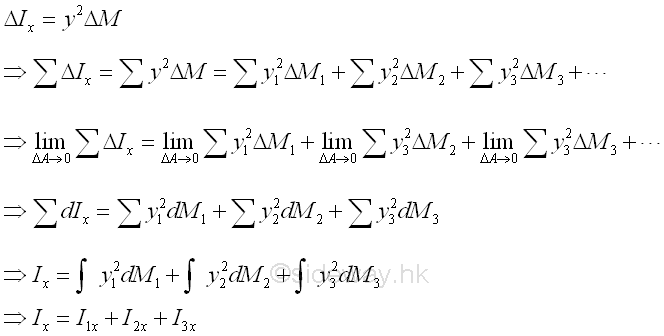
The component body of a composite body is represented by a positive mass while a hollow body is represented by a negative mass. Moment of Inertia of a Mass of Homogeneous Composite BodyMoment of Inertia of Hollow Circular Cylinder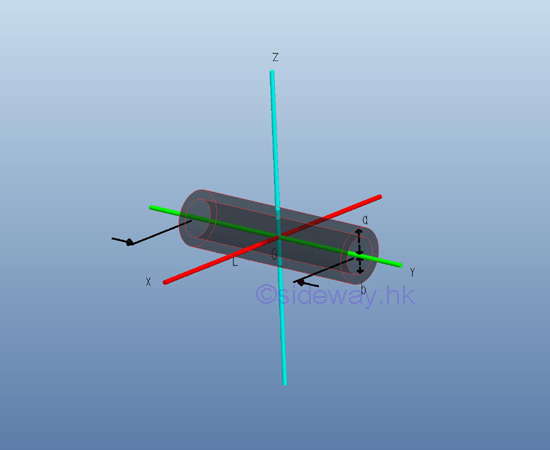
Consider a homogenous hollow circular cylinder of length L with uniform cross-sectional area A of inner radius b, outer radius a and homogenouse material density l. Both the cross-sectional area and the material density are constant over the lenght, the mass and the elemental mass of the hollow circular cylinder can be expressed in terms of the volume of the hollow circular cylinder. Since the cross-sectional radius cannot be neglected, the actual distance between the elemental mass and the reference axis should be used. The moments of inertia about axes x and z, can be determined by the method of composite body. Imply 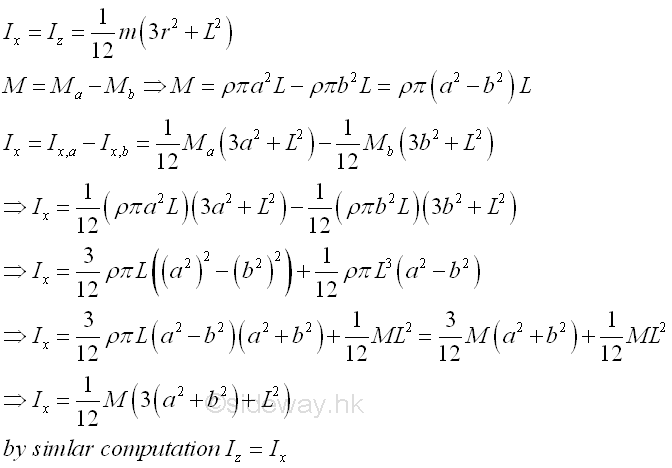
And the moments of inertia about axis y can also be determined by parallel-axis theorem. Imply 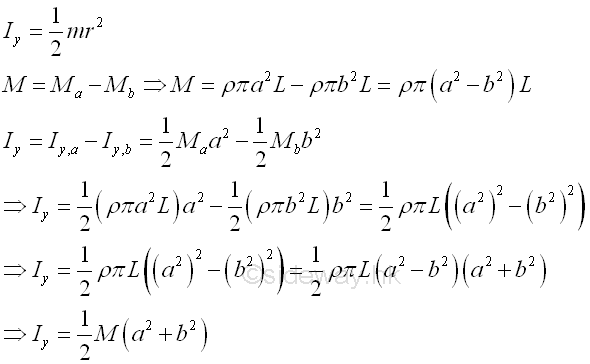
Moment of Inertia of Hollow Sphere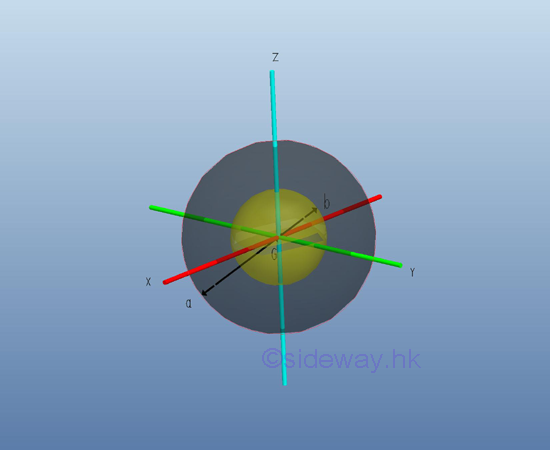
Consider a homogenous hollow sphere of inner radius b, outer radius a and homogenouse material density l. The material density are constant over the lenght, the mass and the elemental mass of the hollow sphere can be expressed in terms of the volume of the hollow sphere. Since the cross-sectional radii cannot be neglected, the actual distance between the elemental mass and the reference axis should be used. The moments of inertia about axes x, y, and z, can be determined by the method of composite body. Imply 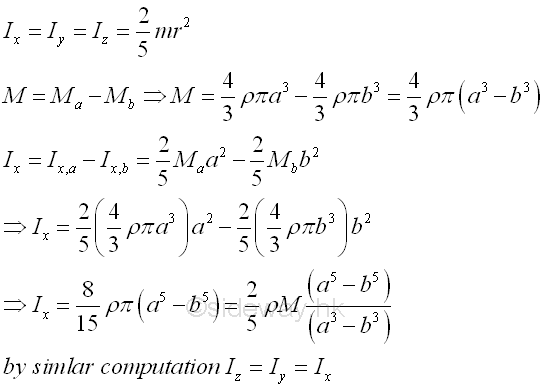
Radius of Gyration of Composite BodySimilar to case of the area moment of inertia, the radius of gyration of a composite body can not be obtained using the radii of gyration of all component bodies of a composite body only. The radius of gyration of a composite body can be determined by the second moment of the composite body and the mass of the composite body directly or making use of the radii of gyration of all component bodies of a composite body together with the masses of the component bodyies of a composite body. Imply 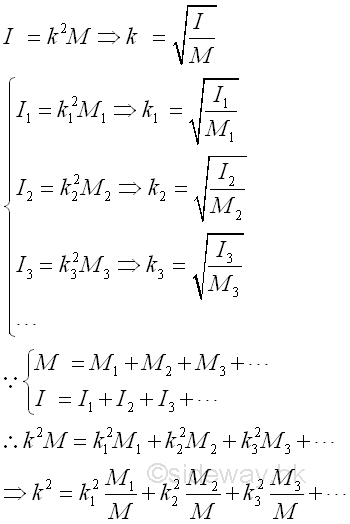
|
Sideway BICK Blog 16/11 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

