 Sideway
BICK BLOG from Sideway
Sideway
BICK BLOG from Sideway
|
Link:http://output.to/sideway/default.asp?qno=121100088 Principal Moments & Product of inertia Principal Moments of InertiaOne of the major interest in the moment of inertia of a body is determining the orientation of the orthogonal axes passing a origin on the body with maximum or minimum moment of inertia about the axes. Product of Inertia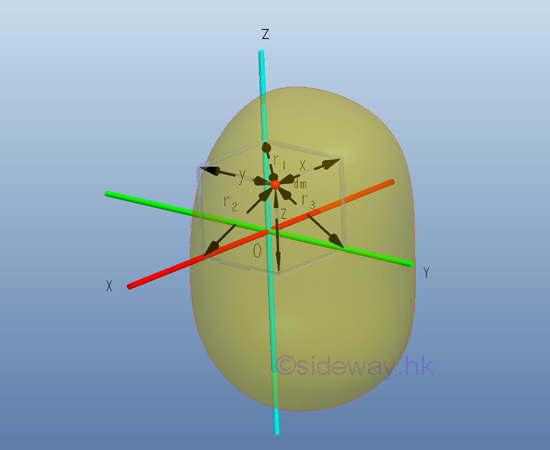
Similar to the product of inertia of an area, a mass product of inertia can also be obtained from an integral over a body of mass m by multiplying the product of the two coordinates, x and y, y and z, and z and x, about the corresponding reference coordinate axes by the elemental mass. Therefore the definition of the mass product of inertia is a little bit different from the definition of the mass moment of inertia in three dimensional space. Imply 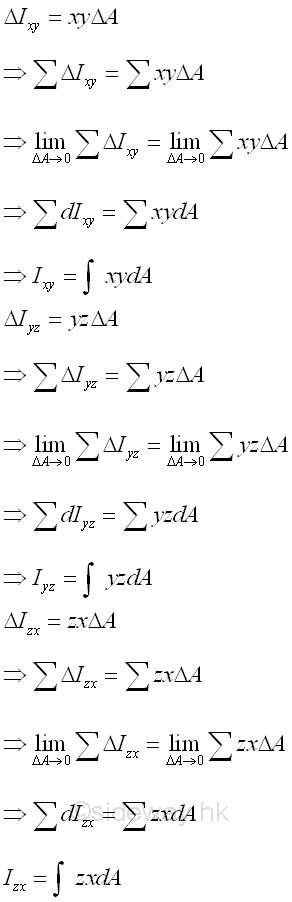
When considering the second moment of a body of mass m as the effect of the first moment acting on the same reference axis, the product moment of a body of mass m can be considered as the cross effect of the first moment acting on the rectangular orthogonal axis through a origin O at the specified rectangular planar orientation with respect to the body. Since the cross effect of the first moment about one rectangular axis will affect the other two rectnagular axes simultaneously, the mass products of inertia a body of mass m in space usually exists in two. Similar to the area product of inertia, the mass product of inertia can be positive, negative, or zero because the value of the paired coordinates, x and y, y and z, and z and x, can be positive, negative, or zero. And similar the first moment of an area about the the axis of symmetry, when one or both of the coordinate planes, pr and qr are the plane of symmetry of the body of mass m, the integral, the mass product of inertia Ipq about the coordinate axes is zero. For example, a cross-sectional plane of a symmetrical elemental body on coordinate axes p=x, q=y, r=z, with plane of symmetry, coordinate plane xz or coordinate plane yz or both. 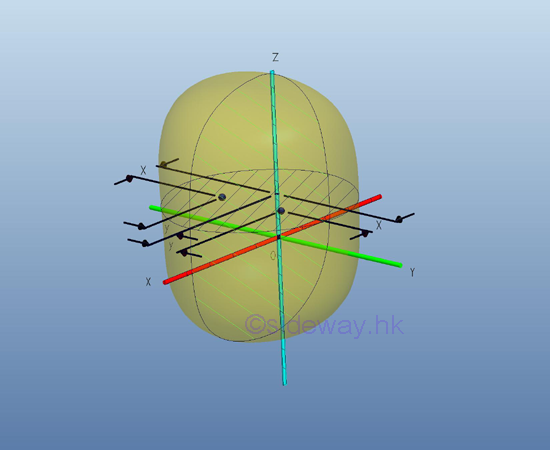
Although the body of mass m is not symmetrical about plane yz, however since the body is symmetrical about plane xz, for any elemental mass at a distance y above the plane xz, there is always an elemental mass below the plane xz at the same mirror location of distance -y below the axis x. Therefore the mass product of inertia of a paired elemental area will cancel out each other and becomes zero, and the integral will reduces to zero also. Imply 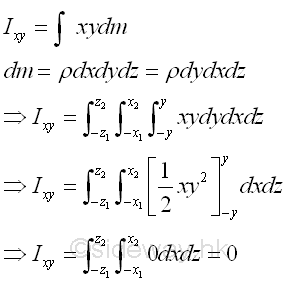
Since the product of inertia of a symmetrical body about one or two planes of symmetry must be zero, the mass product of inertia with respect to planes can be used to test the dissymmetry or imbalance of the body about planes pr and qr because when the mass product of inertia about planes pr and qr is not equal to zero, the body is not symmetrical about both planes pr and qr. But when the mass product of inertia about planes pr and qr is equal to zero, the body may be not symmetrical about planes pr and qr. Parallel-Axis Theorem of Mass Product of InertiaSince the mass product of inertia is evaluated with respect to the cooresponding planes, the parallel-axis theorem of mass product of inertia can be derived similar to the product of inertia of an area. 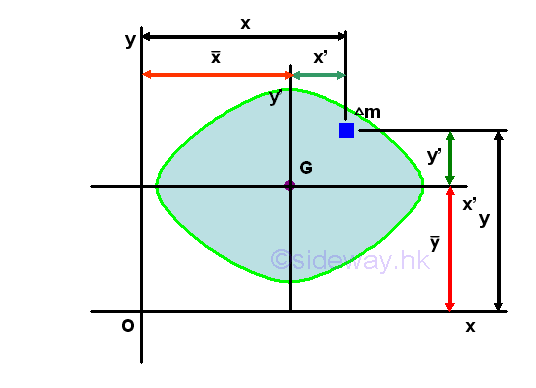
Assume axes x and y are the interested rectangular coordinate axes lying on the planes xz and yz and axes x' and y' are the two rectangular centroidal axes of the body parallel to the coordinate axes lying on plane x'z' and y'z' respectively. Using axes x and y as the system coordinate, the coordinate of the centre of gravity G can be denoted by x and y accordingly and the coordinate of the elemental mass can be denoted by x and y respectively. Therefore the location (x,y) of the elemental mass can also be expressed in terms of the coordinate (x,y) of the centre of gravity G as derived in the parallel-axes theorem for the product of inertia of an area. Imply 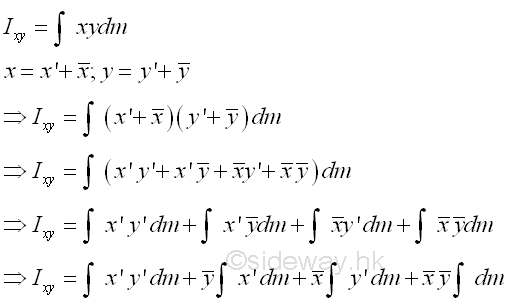
The first integral is the mass product of inertia Ix'y' of the body about the centroidal axes, x' and y' . The second an third integrals are the first moment of the mass m about the centroidal axes, x' and y' and the value of the first moment of the mass m about the centroidal axis is equal to zero. The fourth integral is equal to the total mass m only. Imply 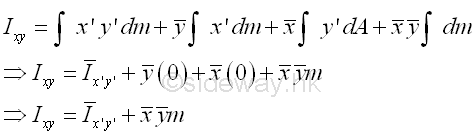
Both the coordinate (x,y) of centre of gravity G of the body and the coodinate (x',y') of the elemental mass dm can be posititve, negative and zero, the mass product of inertia Ixy can therefore also be posititve, negative and zero. Similarly, by substituting the other two pairs of coordinate axes, yz and zx, to the expression, the parallel-axis theorem for the mass products of inertia are 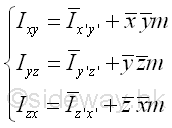
Principal Axes and Principal Moments of InertiaMoment of Inertia about an arbitary axis through O in Space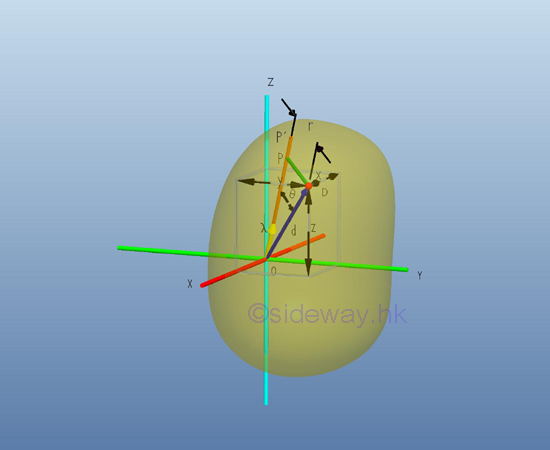
In general, the rectangular moments and product of inertia about an axis at the pole O is depending on the orientation of the axis of which the rectangular moments and product of intertia with respect to. Consider an mass dm is located in space with a system of rectangular coordinate, x, y, and z through the pole O, the rectangular moments and product of inertia of the body with respect to the axes, x, y, and z are 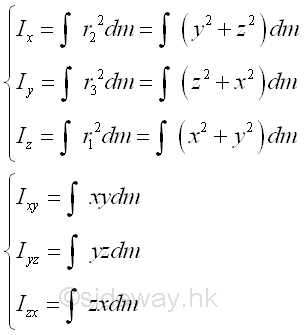
An arbitrary axis OP' can be obtained by tilting about the pole O with the unit direction cosine vector λ. Let the position vector of the elemental mass dm is d, the perpendicaular distance r is equal to r(sin θ) and is equal to the magnitude of the cross product fo vector λ and d, λxd,. The moment of inertia of body with respect to the new axis, OP' is 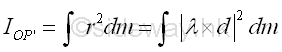
Assume P be a point lying on the axis OP', the line OP can be represented by the parametric equation of line. Imply 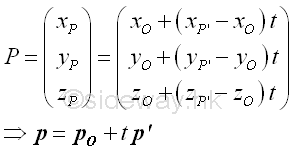
Assume D is the point of the elemental mass dm, the squared distance r2 between points P and Q is 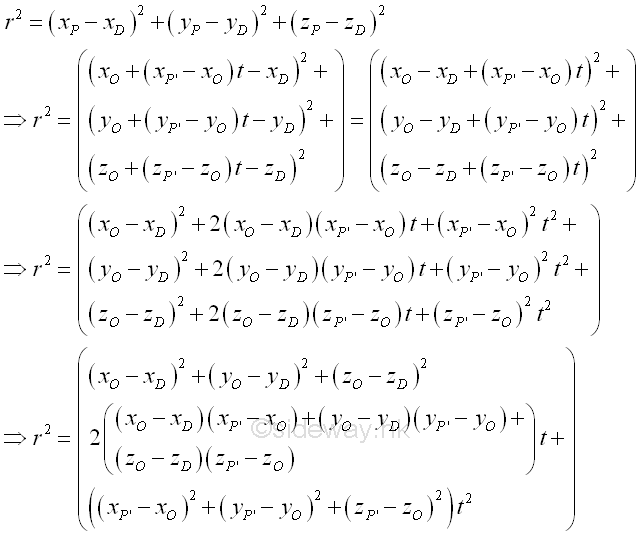
For a perpendicular distance from D to line OP', the distance is minimum. solved by differentiation Imply 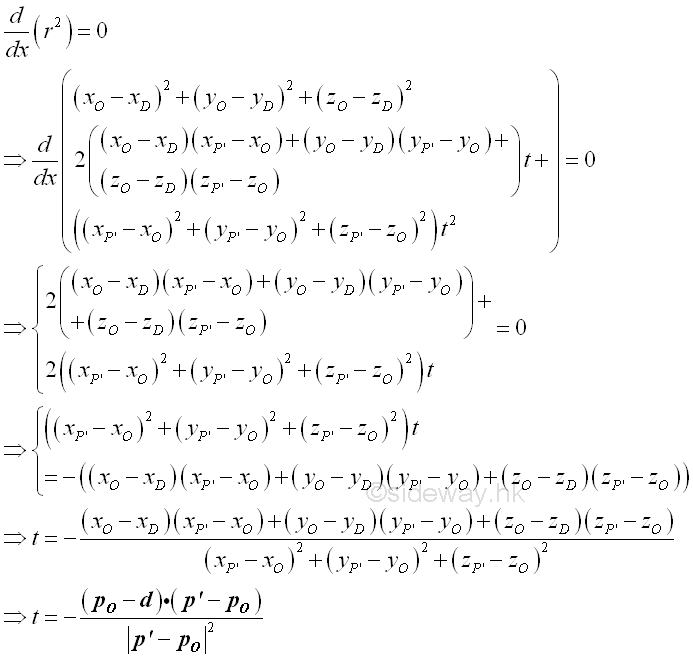
The squared perpendicular distance from D to line OP' can then be obtained by substituting t into the distance equation. Imply 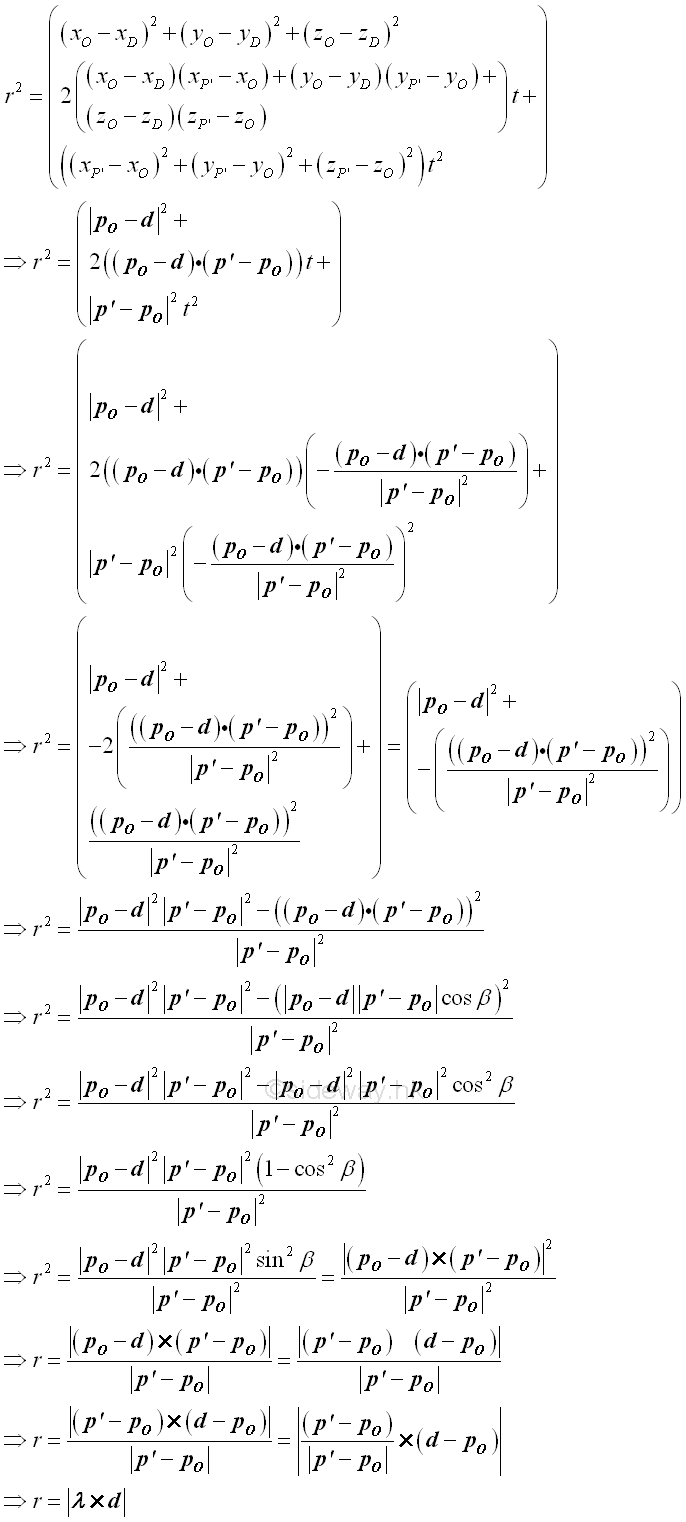
Therefore the perpendicular distance r in terms of the rectangular components of reference coordinate axes is 
The mass moment of inertia about the arbitrary axis OP' can then be expressed in terms of the rectangular components of reference coordinate axes is 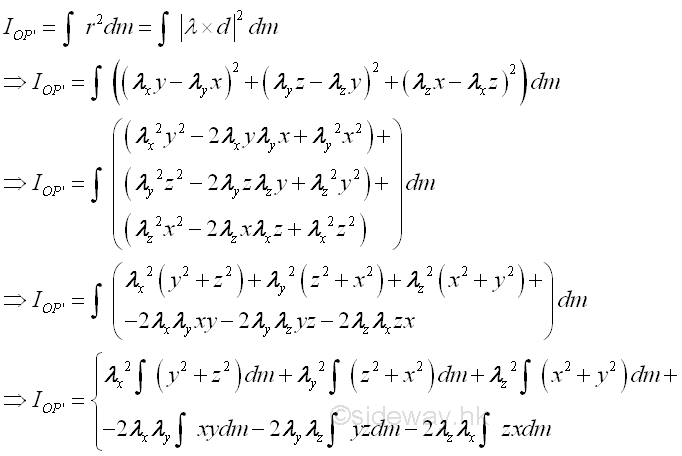
And the mass moment of inertia about the arbitrary axis OP' can therefore be expressed in terms of the rectangular moments and products of inertia about reference coordinate axes. Imply 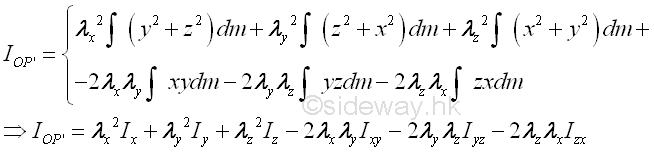
Principal Axes of Moments of Inertia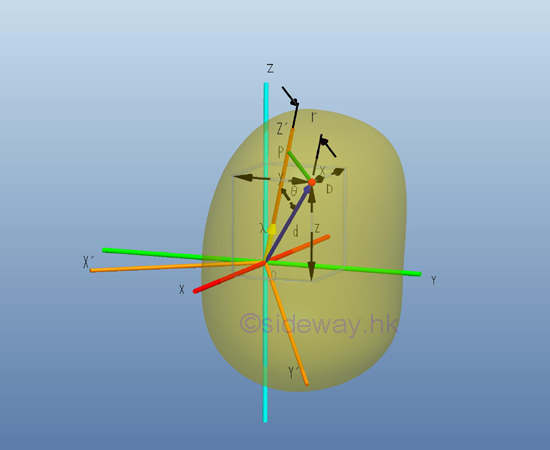
Similar to the rotation of rectangular coordinate axes in area moment of inertia, the rectangular coordinate axes can also be freely rotated in space. Consider the rectangular mass moments of inertia about a pole, the origin O, and by definition the mass moments of inertia can be expressed in terms of the distance of the elemental mass from the pole. Imply 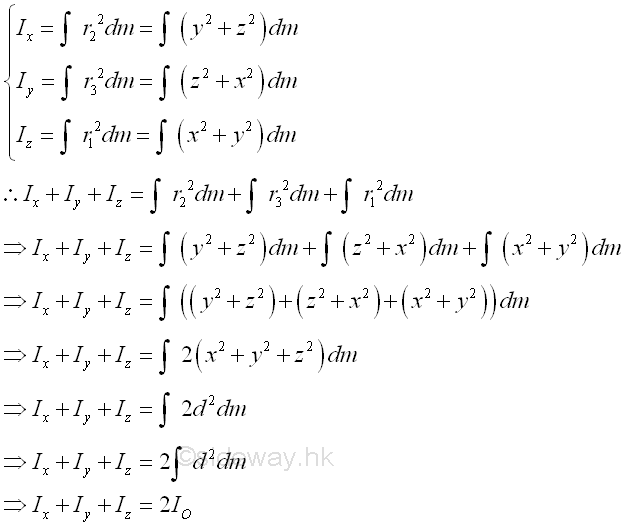
Since the rectangular moments of inertia is always positive and the distance between an elemental mass and the origin does not change with the rotation of the rectangular coordinate axes, the sum of the rectangular mass moments of inertia about the rectangular coordinate axes through a origin through a coordinate system rotation is invariant. For the product of inertia, the rectangular coordinate axes rotation will cause changes in both the valuse and signs of the products of inertia as the change in the angle of rotation. For example, consider a coordinate rotation of axes about the z-axis, the mass product of inertia can be evaluated as in the area product of inertia similarly with the angle of rotation is the angle of rotation on the corresponding plane respectively. Imply 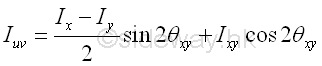
Therefore a rotation of 90o about the z-axis will reverse the sign of Ixy. and a rotation of 180o about the z-axis will only reverse the sign of Iyz and Izx because of the positive of x and y axes are reversed while the sign of Ixy. remains unchanged. Since the change of rotation angle can be varied smoothly, there is always an angle of orientation that the product of inertia is equal to zero. Similarly, another two angle of orientation that the product of inertia is equal to zero can also be located on the other two rectangular coordinate axes. Since the change of direction cosines can be varied smoothly in space, It is always possible to orientate the rectangular coordinate axes system relative to a given body with known rectangular moments of inertia about the given rectangular coordinate system. The three mutually orthogonal coordinate axes x', y' and z' through O, with products of inertia equal to zero are called the principal axes of moments of inertia through O. If origin O is the centre of gravity of the body, the principal axes are called central principal axes. Ellipsoid of Inertia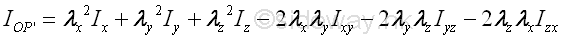
According to the equation of the moment of inertia about an arbitary axis through O, the value of the moment of inertia about an artbitary axis through O is a function of the direction cosines. Since the rectangular moments of inertia are always greater than zero and the sum of the rectangular moments of inertia about a reference pole is invariant, the moment of Inertia about an arbitary axis through O in space is limited. For the rectangular moments of inertia, the coefficients, squared direction cosines, are alway positive. But for the products of inertia , the coefficients, 2 times product of direction cosines, are varied smoothly between 2 and -2, similar to the case in the product of inertia of an area. Graphically, the moments of inertia of a body about the rectangular axes through a reference point can be plotted in term of a point R on the rectangular coordinate axes system with known rectangular moments of inertia. Let IOP'=kOP'2 m=1/ROR2 ⇒ROR=1/√IOP' = 1/kOP'√m , where kOP' is the radius of gyration about the reference axis, then the moment of inertia about an axis with direction cosine λ can be repsented by a corresponding point with the corresponding direction cosine f on the coordinate axes system, where R is the distance from the point to the origin O. The equation of moment of inertia becomes 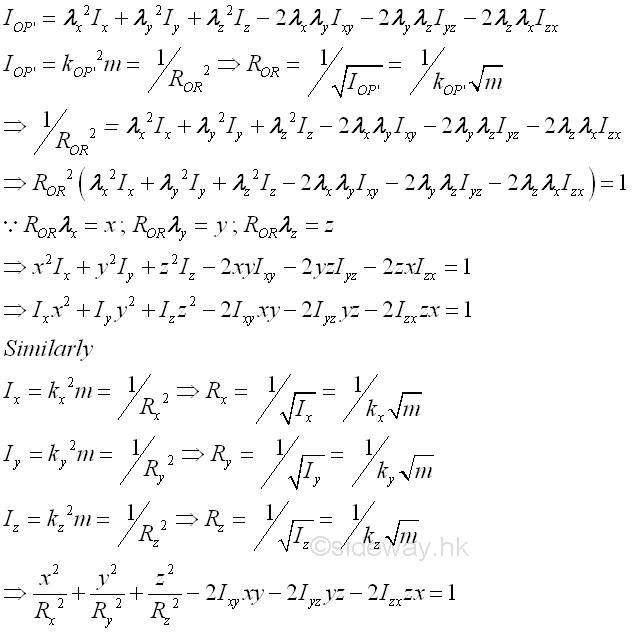
Therefore, the plot of the moment of inertia about all possible axes through the refence point O from the equation of the moment of inertia by varying the direction cosines in space represented by the locus of R is in the form of an ellipsoid surface. Imply 
Since the magnetude of ROR is proportion to the reciprocal of the radius of gyration only which is depending on the location of the reference axis relative to the body itself, the value of ROR does not change with the position or orientation of the body in space, that is not depending on the choice of the rectangular coordinate axes system. Therefore the ellipsoid surface can be fixed to the body at a fixed orientation relative to the body and the ellipsoid surface is the ellipsoid of inertia about the origin O of the body. If the origin O is same as the centre of gravity, the ellipsoid of inertia is called the principal ellipsoid of inertia. Principal Moments of InertiaIn other words, when considering the rectangular coordinate axes system xyz, the ellipsoid surface is crooked and tilted at an angle to the rectangular coordinate principal axes system x'y'z' with the quadric surface equation 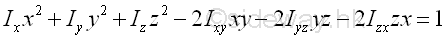
where the direction cosines, rectangular moments and products of inertia are evaluated with respect to the rectangular coordinate axes system xyz. However when considering the rectangular coordinate principal axes system x'y'z', the quadric surface equation becomes the standard equation. Imply 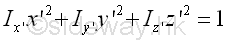
where the direction cosines, and rectangular moments are evaluated with respect to the rectangular coordinate principal axes system x'y'z'. By comparing with the ellipsoid surface equation, the products of inertia with respect to principal axes system x'y'z' should be equal to zero. By similar procedures with reverse substitution, the moment of inertia about an arbitary axis through O with respect to the rectangular coordinate principal axes system in space becomes 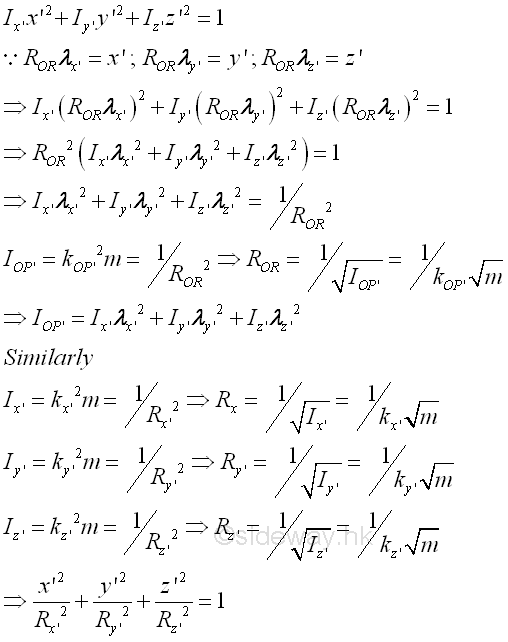
Since the products of inertia about the principal axes of the rectangular coordinate principal axes system through O in space are equal to zero, the moments of inertia, Ix', Iy', and Iz' about the principal axes are the principal moments of inertial through O. If origin O is the centre of gravity of the body, the principal moments of inertia are called central principal moments of inertia. Principal Axes and Principal Moments of Inertia DeterminationBody with plane of symmetryIn general, the principal axes of a body can be determined by the plane of symmetry, since the product of inertia about the plane of symmetry is always equal to zero. For example, the planes of symmetry of a shpere always pass through the centre of sphere. Any two mutually perpendicular planes passing through the centre of sphere would be two mutually perpendicular planes of symmetry and all of the products of inertia are zero also. Including these two mutually perpendicular planes of symmetry, the coordinate axes along the intersection of the three mutually perpendicular planes are then the principal axes of moments of inertia. And the planes of symmetry of a right cone of elliptical base always passing through a semi-principal axis of the elliptic base and the central axis. The coordinate axis along the intersection of the two mutually perpendicular planes of symmetry is the principal axis of moments of inertia. Including these two mutually perpendicular planes of symmetry, the coordinate axes along the intersection of the three mutually perpendicular planes are then the principal axes of moments of inertia. And the planes of symmetry of a regular tetrahedron always passing through an edge of the tetrahedron and an axis through a vertex and perpendicular to the opposite plane. Since the shape remains unchange after a rotation of the regular tetraedron about the axis by 120 degree, the axis is a principal axis and the ellipsoid of inertia along the axis remains unchanged under this rotation, i.e. the ellipsoid of inertia is a circle. Therefore any axis along the intersection of the two mutually perpendicular planes perpendicular to the axis of the principal axis is another principal axis. For a regular tetrahedron or polyhedron, when considering another vertex, same ellipsoid of inertia along the axis is obtained respectively. And therefore the ellipsoid of inertia through the centre of gravity of a regular tetrahedron is a sphere. Body of arbitary shapeIf there is no obvious property of symmetry on the body under evaluation, the principal axes and the principal moments of inertia at point O can be determined from the known ellipsoid of inertia with respect to a rectangular coordinate axes system with origin at point O by the method of vector differential calculus. 
Since the ellipsoid of inertia of a body only depends on the orientation of the body and the given origin, and not depends on orientation of the rectangular coordinate axes system, all equations of quadric surface derived from the body at the origin O are describing the same ellipsoid surface of the ellipsoid of inertia of the body at the point O. As the principal axes of the moment of inertia always coincides with the semi-principal axes of the ellipsoid, the radius vectors ROR of points on the principal axes are always collinear with the normal vector of the ellipsoid surface. The direction of vertor n at a point R normal to the ellipsoid surface of function can be obtained by the gradient ∇f of the function f at point R. The equation of the ellipsoid surface provides fixed relations between the coordinates x, y and z, the ellipsoid surface can also be described by the locus of a scalar function f(x,y,z), a function of coordinates x, y, and z in space as a level surface by setting the function f(x,y,z) equal to a constant. Therefore the ellipsoid surface can also be respresented a level surface f(x,y,z)=c, e.g. f(x,y,z)=0. The equation. Imply 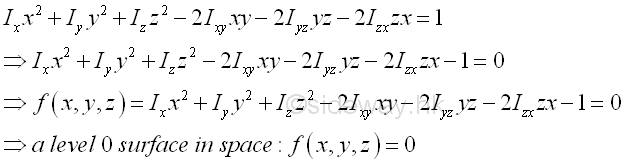
If a parametric curce C(t)=x(t)i+y(t)j+z(t)k lies on the ellipsoid surface, then function x(t), y(t), and z(t) also lies in the ellipsoid surface also. Imply 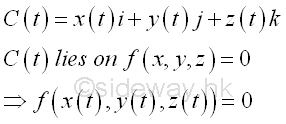
By differentiating the equation with respect to t and by chain rule. Imply 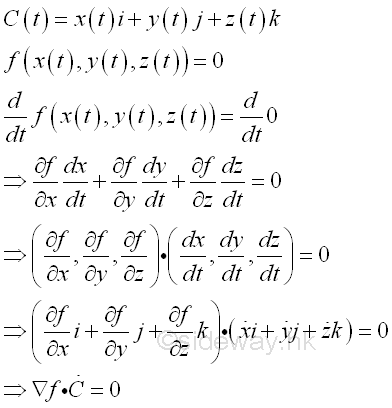
Since the dot product of two vectors is equal to zero when the two vectors are orthogonal, and dC/dt is always tangent to the curve C or tangent to the surface f, the gradient ∇f of function f must normal to the surface. Imply 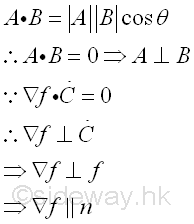
In other words, the gradient ∇f of function f(x,y,z) of the ellipsoid surface can be the normal vector n at any point with coordinate (x,y,z) on the ellipsoid surface. And the locus vector of the ellipsoid surface is equal to R(x,y,z) at any point with coordinate (x,y,z) on the ellipsoid surface. Since vectors ∇f and R are collinear at point R(x,y,z) of different magnitude, two vectors can be equated by multiplying one vector with a constant, e.g. 2K, imply 
In order to have non-trivial solution, i.e. λx0 and fy0 and λz0, the discriminant of the system of equations must be vanish, i.e. the determinant of the coefficients should equal to zero. Imply 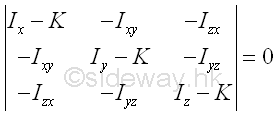
Expanding the determinant. Imply 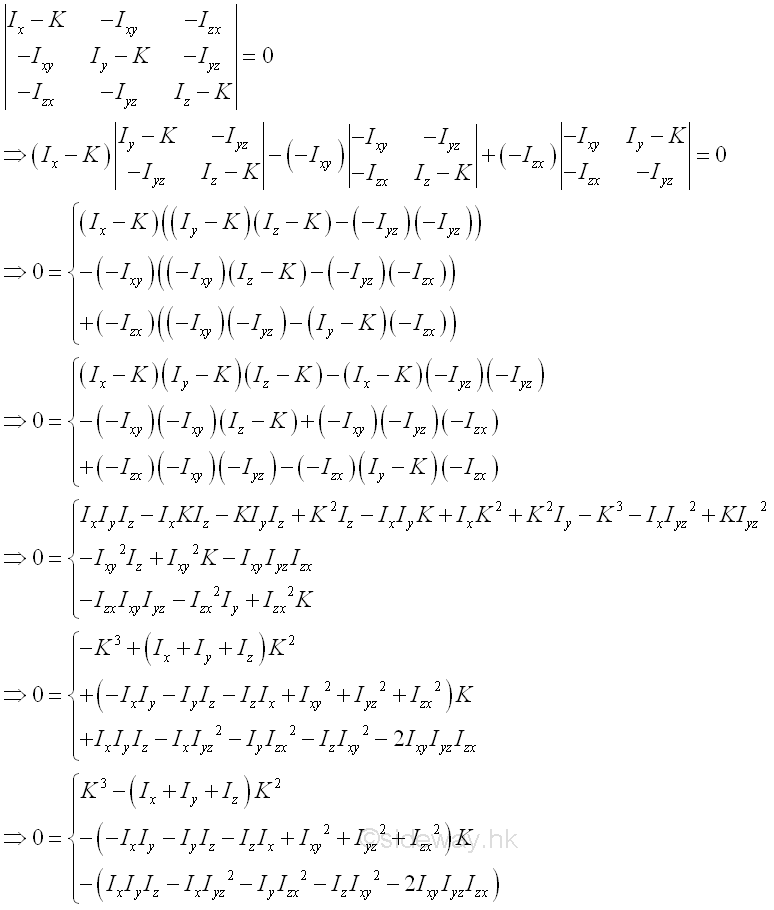
The determinant leads to the secular or characteristic equation of cubic order in K, which yields three real, positive roots or eigenvalues, i.e. K1, K2, and K3. Each root can therefore represent a moment of inertia about the corresponding principal axis of the ellipsoid surface. For example, substitute K1, for K in the system of equations. Imply 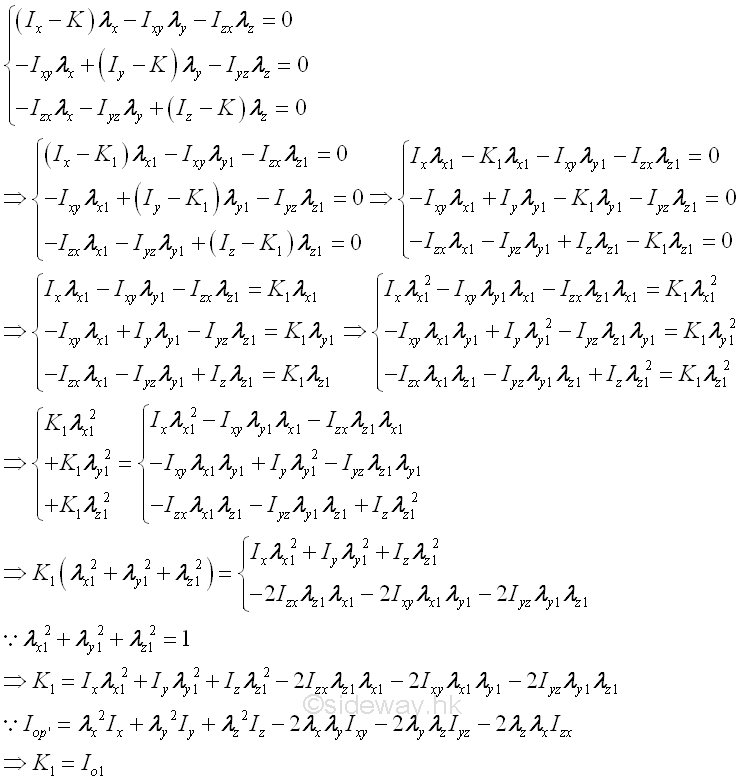
Since the system of equations are linearly dependent after substituting the roots or eigenvalues to the system of equations, only two of the system of equations are used to determine the direction cosines, λx, fy, and λz with free variable by Gauss elimination or rows reduction. |
Sideway BICK Blog 17/11 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

