Product of Matrices
Product of Matrices,

Let
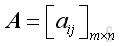 ,
,
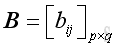 and
and
 ,
,
for matrix
A
of order m x n,and matrix
B
of order p x q, product of matrices exist if and only if
 . Then the product of matrices is
. Then the product of matrices is
 where the order of matrix
D
is x by y and
where the order of matrix
D
is x by y and
 ,
,
 .
The elements of
D are
.
The elements of
D are
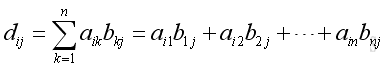
Or

For example,

From the definition of matrix multiplication, it is possible to have
 without
without
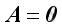 or
or
 and
and
 without
without
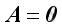 or
or
 .
.
Properties of Matrix Multiplication
If both matrix B
premultiplied by matrix
A,
 and matrix
B
postmultipled by matrix
A,
and matrix
B
postmultipled by matrix
A,
 are defined,
are defined,
 . In general, matrix multiplication is not commutative.
. In general, matrix multiplication is not commutative.
 . Multiplication of matrices is associative.
. Multiplication of matrices is associative.
For matrix
A
of order m x n, matrix
B
of order p x q and matrix
C
of order s x t, product of matrices exist if and only if
 and
and  . Then element of
. Then element of
 is
is

And the element of
 is
is

Rearrange the order of terms

And equals to the element of
 or
or
 .
.
Matrix multiplication is distributive with respect to addition.
If
 , then
, then
 and
and
 .
.
If A
and D
are of same order and
B
and C
are square matrices, then
A,
B,
C
and D
are all square matrices.
Since
 equals
equals
 and the element is
and the element is

And equals to the element of
 .
.
Identity Matrix
The identity under matrix multiplication is the identity matrix, that is

Let
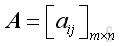 ,
,
 and
and
 then
then

and

In order to have the same order as
A,
for element x, order of k should equal to i and for
element y, order of l should equal to j, and therefore
the identity matrix must be square.
According to the equality of matrices,
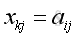 only when
only when
 ,
and
,
and
 only when
only when
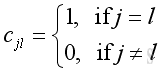 .
.
The form of identity matrix is
 .
.
If
 , that is
, that is
 , then
A
must be a square matrix.
, then
A
must be a square matrix.
And therefore it is also called unit matrix.
Inverse Matrix
If A
has an multiplication inverse
 and
and
 then
A
must be square.
then
A
must be square.
If a matrix has an inverse, the inverse is unique.
Assume both B
and C
are inverses of A,
then
 and
and
 .
.
Premultiply first equation by
C,
imply
 .
.
From second equation, imply
 and the inverse is unique.
and the inverse is unique.
Division of matrices has not been defined, the multiplying of the
reciprocal of a matrix can be replaced by multiplying the inverse of the matrix.
Therefore solving
B
in
 can be obtained by premultiplying
can be obtained by premultiplying
 .
.

Let
 , If both matrices have an inverse, then
, If both matrices have an inverse, then
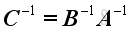 . That is
. That is

The inverse of a matrix's inverse equals to the matrix itself,
 . Let
. Let
 then
then

Transpose of a matrix
Transpose of a matrix,
 or
or
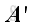
The transpose of a matrix, written as
 , is obtained by interchanging the rows and
columns of the original matrix
A.
Therefore if
, is obtained by interchanging the rows and
columns of the original matrix
A.
Therefore if
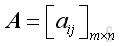 amd
amd
 , the elemnt,
, the elemnt,
 of matrix
of matrix
 equals to the element,
equals to the element,
 of matrix,
A.
And if the order of
A
is m x n then the order of
of matrix,
A.
And if the order of
A
is m x n then the order of
 is n x
m.
is n x
m.
For example,

Properties of Matrix Transpose
 , if and only if
, if and only if
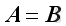 .
.



Matrix Products Transpose
if the matrix multiplication of
 exists, then
exists, then
 .
.
Since
 is defined,
is defined,
 is also defined while
is also defined while
 may not be.
may not be.
Let
 , where
A
is of order m x n and
B
is of order n x r, and
C
is of order m x r then
, where
A
is of order m x n and
B
is of order n x r, and
C
is of order m x r then
 and element of
C is
and element of
C is

Let D
is the transpose of
C,
then

That is element in the row j and colume
i of matrix
D
equals to product of row i of matrix
A
and column j of matrix
B,
that is

Let
 , since
, since
 is of order n x
m and
is of order n x
m and
 is of order r x
n, then
E
is of order r x m.
is of order r x
n, then
E
is of order r x m.
Let X
be the transpose of
A, imply
 ,
,
Let Y
be the transpose of
B,
imply

and imply
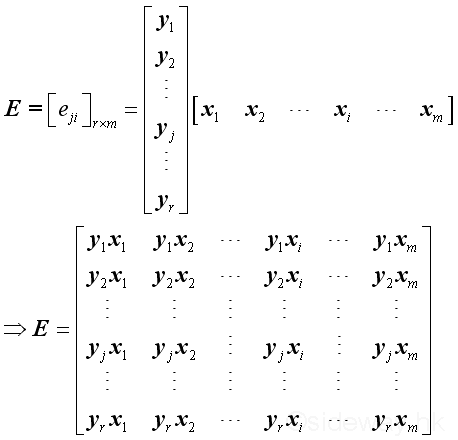 ,
,
That is element in the row j and colume
i of matrix
E
equals to
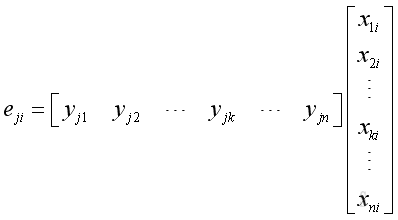 ,
,
Subsitute corresponding elements in row of matrix
B
and in column of matrix
A
imply
 ,
,
And equals to the element of
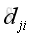 .
Therefore
.
Therefore

Transpose of Inverse Matrix
If
 exists, then
exists, then
 .
Since
.
Since
 and
and
 , imply
, imply
 ,
,
 Sideway
BICK BLOG from Sideway
Sideway
BICK BLOG from Sideway Sideway
BICK BLOG from Sideway
Sideway
BICK BLOG from Sideway