Sideway BICK BLOG from Sideway

A Sideway to Sideway Home

Script, Scripting Language, VBScript elements, Server-Side VBScript Function, Math Function, Derived Math Function

VBScript Derived Math Functions

Some common non-intrinsic math functions can be derived from the intrinsic vbs math functions

‎Mathematical Constants

Examples of ‎mathematical constants

Constant π

ASP VbScript Command:

<script runat="server" language="VBScript">
Dim pi:pi= 4*Atn(1)
Response.Write "π≈pi=4*Atn(1)="&pi&"<br />"
</script>

HTML Web Page In-line Output:

π≈pi=4*Atn(1)=3.14159265358979

Constant e

ASP VbScript Command:

<script runat="server" language="VBScript">
Dim e:e= Exp(1)
Response.Write "e=e^1≈Exp(1)="&e&"<br />"
</script>

HTML Web Page In-line Output:

e=e^1≈Exp(1)=2.71828182845905

‎Trigonometric Functions

Examples of ‎trigonometric functions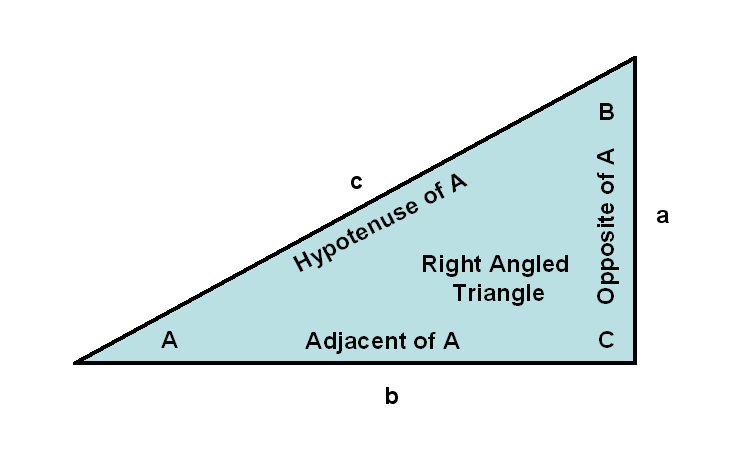

Function (let c=1)Mathematical EquationDerived equivalent Secant function, sec(A)=c/bsec(A)=1/cos(A)1/Cos(A) Cosecant function, csc(A)=c/acsc(A)=1/sin(A)1/Sin(A) Cotangent function, cotan(A)=b/acotan(A)=1/tan(A)1/Tan(A) Inverse sine function, A=arcsin(a/c)= arcsin(a)A=arcsin(a/c)=arctan(a/b)= arctan(a/(c^2-a^2)^0.5)Atn(a/Sqr(-a*a+1)) Inverse cosine function, A=arccos(b/c)= arccos(b)A=arccos(b/c)=arccotan(b/a)= π/2-arctan(b/(c^2-b^2)^0.5)= arctan(-b/(c^2-b^2)^0.5)+π/2Atn(-b/Sqr(-b*b+1))+2*Atn(1) Inverse secant function, A=arcsec(c/b)A=arcsec(c/b)=π/2-arccsc(c/b)2*Atn(1)–Atn(Sign(x)/Sqr(x*x–1)) Inverse cosecant function, A=arccsc(c/a)A=arccsc(c/a)=arctan(a/b)= arctan(a/(c^2-a^2)^0.5)= arctan(Sign(c/a)/((c/a)^2-1)^0.5)Atn(Sgn(c/a)/Sqr((c/a)*(c/a)–1))= Atn(Sign(x)/Sqr(x*x–1)) Inverse cotangent function, A=arccotan(b/a)A=arccotan(b/a)= π/2-arctan(b/a)2*Atn(1)-Atn(b/a)= 2*Atn(1)-Atn(x)

Hyperbolic Functions

Examples of hyperbolic functions

FunctionMathematical EquationDerived equivalent Hyperbolic sine sinh(x)(e^x-e^-x)/2(Exp(x)–Exp(-x))/2 Hyperbolic cosine cosh(x)(e^x+e^-x)/2(Exp(x)+Exp(-x))/2 Hyperbolic tangent tanh(x)(e^x-e^-x)/(e^x+e^-x)(Exp(x)–Exp(-x))/(Exp(x)+Exp(-x)) Hyperbolic secant sech(x)2/(e^x+e^-x)2/(Exp(x)+Exp(-x)) Hyperbolic cosecant csch(x)2/(e^x-e^-x)2/(Exp(x)–Exp(-x)) Hyperbolic cotangent coth(x)(e^x+e^-x)/(e^x-e^-x)(Exp(x)+Exp(-x))/(Exp(x)–Exp(-x)) Inverse hyperbolic sine arcsinh(x)ln(x+(x^2+1)^0.5)Log(x+Sqrt(x*x+1)) Inverse hyperbolic cosine arccosh(x)ln(x+(x^2-1)^0.5)Log(x+Sqrt(x*x–1)) Inverse hyperbolic tangent arctanh(x)ln((1+x)/(1-x))/2Log((1+x)/(1–x))/2 Inverse hyperbolic secant arcsecH(x)ln(1/x+(1/x^2-1)^0.5)= ln((1+(1-x^2)^0.5)/x)Log((Sqr(-x*x+1)+1)/x) Inverse hyperbolic cosecant arccsch(x)ln(1/x+(1/x^2+1)^0.5)= ln((1+Sign(x)*(1+x^2)^0.5)/x)Log((Sgn(x)*Sqr(x*x+1)+1)/x) Inverse hyperbolic cotangent arccoth(x)ln((x+1)/(x-1))/2Log((x+1)/(x–1))/2

‎Logarithm Functions

Examples of ‎logarithm functions

Logarithm Functions

ASP VbScript Command:

<script runat="server" language="VBScript">
Dim e:e=Exp(1)
Dim ln_e:ln_e=log(Exp(1))
Response.Write "Log(x): The natural logarithm of x has the number e (≈ 2.718) as its base."&"<br />"
Response.Write "Log(x):Logarithm of x to base e:"&"<br />"
Response.Write "e=Exp(1)="&e&"<br />"
Response.Write "ln_e=log(e)="&ln_e&"<br /><br />"
Dim ten:ten=10^1
Dim log10_10:log10_10=log(10)/log(10)
Response.Write "Log10(x): The common logarithm of x has the number 10 as its base."&"<br />"
Response.Write "Log10(x):Logarithm of x to base 10:"&"<br />"
Response.Write "ten=10^1="&ten&"<br />"
Response.Write "log10_10=log(10)/log(10)="&log10_10&"<br />"
Dim hundred:hundred=10^2
Dim log10_100:log10_100=log(100)/log(10)
Response.Write "hundred=10^2="&hundred&"<br />"
Response.Write "log10_100=log(100)/log(10)="&log(100)&"/"&log(10)&"="&log10_100&"<br /><br />"
Response.Write "LogN(x): The logarithm of x has the number N as its base."&"<br />"
Response.Write "LogN(x):Logarithm of x to base N=Log(x)/Log(N)"&"<br />"
</script>

HTML Web Page In-line Output:

Log(x): The natural logarithm of x has the number e (≈ 2.718) as its base.
Log(x):Logarithm of x to base e:
e=Exp(1)=2.71828182845905
ln_e=log(e)=1

Log10(x): The common logarithm of x has the number 10 as its base.
Log10(x):Logarithm of x to base 10:
ten=10^1=10
log10_10=log(10)/log(10)=1
hundred=10^2=100
log10_100=log(100)/log(10)=4.60517018598809/2.30258509299405=2

LogN(x): The logarithm of x has the number N as its base.
LogN(x):Logarithm of x to base N=Log(x)/Log(N)

Sources

MAR 2018

S	M	T	W	T	F	S

				1	2	3
4	5	6	7	8	9	10
11	12	13	14	15	16	17
18	19	20	21	22	23	24
25	26	27	28	29	30	31

JAN 2010

S	M	T	W	T	F	S

					1	2
3	4	5	6	7	8	9
10	11	12	13	14	15	16
17	18	19	20	21	22	23
24	25	26	27	28	29	30
31

Sideway BICK Blog

14/03