Sideway BICK BLOG from Sideway

A Sideway to Sideway Home

Moment of Inertia of an Area

Second Moment of An Area of Geometric Shape

The second moment of an area of a geometric shape can be determined by integration or the parallel-axis theorem. Imply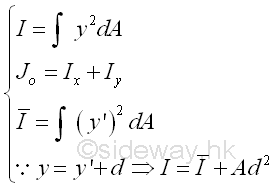

Moment of Inertia of Areas

Second Moment of Area of Rectangle

Second Moment about x' by Double Integration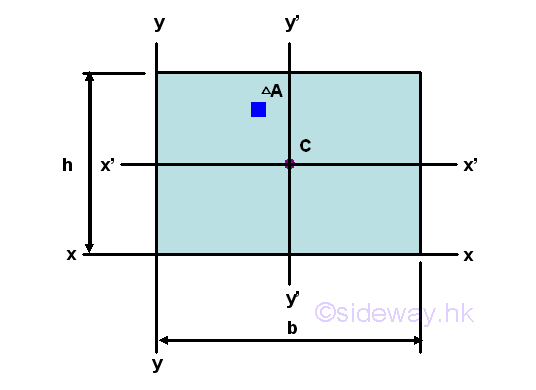

The second moment of an area of a rectangle about the centroidal axis x' is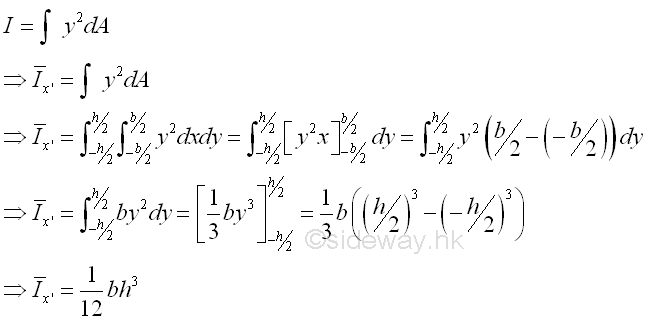

Second Moment about y' by Single Integration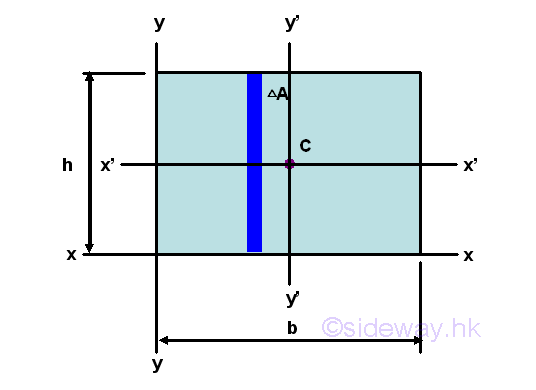

The second moment of an area of a rectangle about the centroidal axis y' is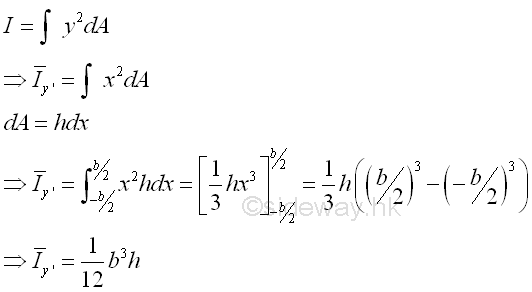

Second Moment about x by Parallel-Axis Theorem

The second moment of an area of a rectangle about the axis x is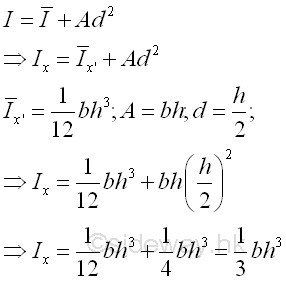

Second Moment about y by Parallel-Axis Theorem

The second moment of an area of a rectangle about the axis y is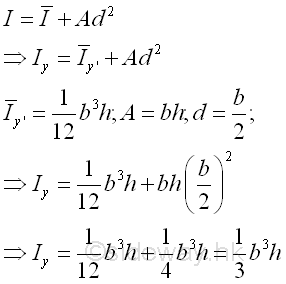

Polar Moment about C from Rectangular Moments of Inertia

The polar moment of an area of a rectangle about the centroid C is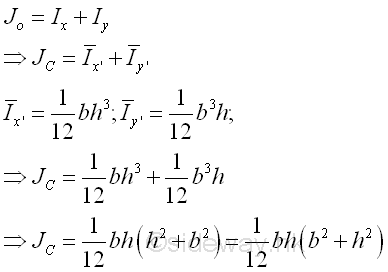

Second Moment of Area of Circle

Second Moment about x' by Double Integration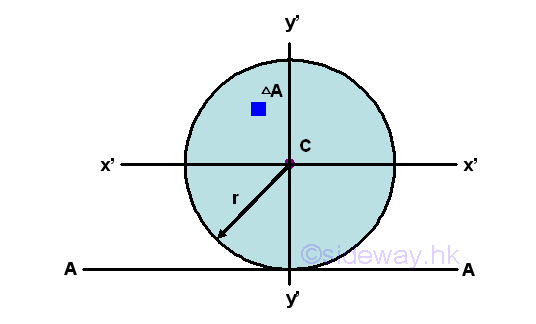

The second moment of an area of a circle about the centroidal axis x' is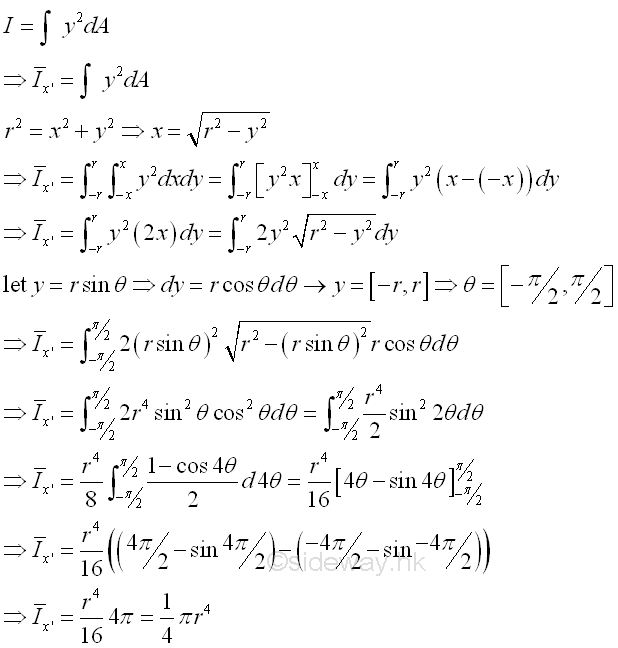

Second Moment about y' by Double Integration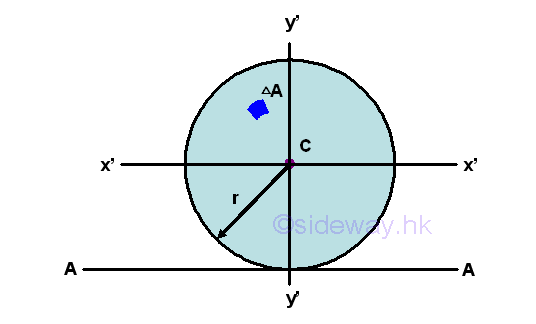

The second moment of an area of a circle about the centroidal axis y' is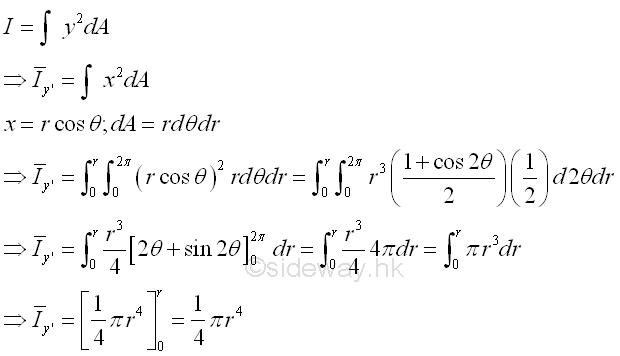

Polar Moment about C from Rectangular Moments of Inertia

The polar moment of an area of a circle about the centroid C is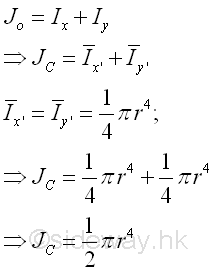

Second Moment about A by Parallel-Axis Theorem

The second moment of an area of a rectangle about axis A is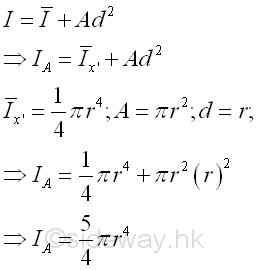

Second Moment of Area of Triangle

Second Moment about x' by Single Integration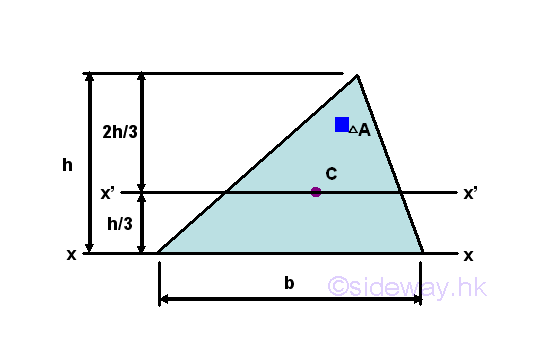

The second moment of an area of a triangle about the centroidal axis x' is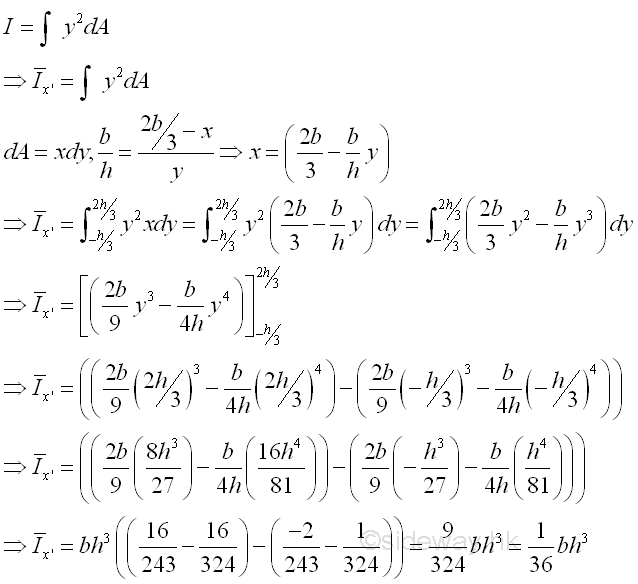

Second Moment about x by Parallel-Axis Theorem

The second moment of an area of a triangle about the axis x is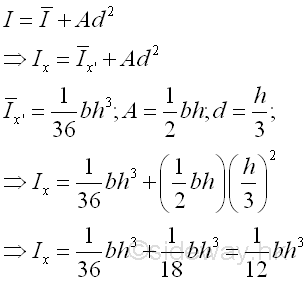

Link:http://output.to/sideway/default.asp?qno=121000006

FontForge

FontForge is a outline and bitmap font editor from http://sourceforge.net/projects/fontforge/ by fontforge.org.

The graphic user interface of FontForge from http://sourceforge.net/projects/fontforge/ :

Site of FontForge

FontForge http://fontforge.org/ last updated 7/22/2017
FontForge – An Outline Font Editor download | SourceForge.net https://sourceforge.net/projects/fontforge/?source=navbar last updated 7/22/2017
FontForge Open Source Font Editor http://fontforge.github.io/en-US/ last updated 7/22/2017

Links of FontForge

A meandering bibliography of font related things http://fontforge.github.io/bibliography.html last updated 7/27/2017
acorn2sfd -- A program for comparing fonts http://fontforge.github.io/acorn2sfd.html last updated 7/27/2017
Bézier Splines http://fontforge.github.io/bezier.html last updated 7/27/2017
Bitmap Character View http://fontforge.github.io/bitmapview.html last updated 7/27/2017
Bitmap strikes http://fontforge.github.io/editexample8.html last updated 7/27/2017
Building accented glyphs http://fontforge.github.io/editexample4.html last updated 7/27/2017
Command Line Arguments http://fontforge.github.io/cliargs.html last updated 7/27/2017
Consistent serifs and stem widths http://fontforge.github.io/editexample3.html last updated 7/27/2017
Contextual features http://fontforge.github.io/editexample6-5.html last updated 7/27/2017
Creating a glyph using spiro points http://fontforge.github.io/editspiro.html last updated 7/26/2017
Creating the letter "o" -- consistant directions http://fontforge.github.io/editexample2.html last updated 7/27/2017
Documentation http://fontforge.github.io/en-US/documentation/ last updated 7/22/2017
Error Recovery http://fontforge.github.io/errrecovery.html last updated 7/27/2017
Examining and controling metrics and kerning http://fontforge.github.io/editexample5.html last updated 7/27/2017
File List http://fontforge.github.io/nvd.html last updated 7/27/2017
Files used by FontForge http://fontforge.github.io/files.html last updated 7/27/2017
Final cleanup http://fontforge.github.io/editexample7.html last updated 7/27/2017
Font database files for FontForge http://fontforge.github.io/sfds/index.html last updated 7/27/2017
Font Info http://fontforge.github.io/fontinfo.html last updated 7/27/2017
FontForge – An Outline Font Editor - Browse /fontforge-source at SourceForge.net https://sourceforge.net/projects/fontforge/files/fontforge-source/ last updated 7/27/2017
FontForge -- An outline font editor for PostScript®, TrueType and OpenType fonts http://fontforge.github.io/overview.html last updated 7/26/2017
FontForge install procedures for cygwin (MS/Windows) http://fontforge.github.io/ms-install.html last updated 7/27/2017
FontForge install procedures for unix/linux based systems http://fontforge.github.io/nix-install.html last updated 7/27/2017
FontForge Scripting Tutorial http://fontforge.github.io/scripting-tutorial.html last updated 7/27/2017
FontForge's math http://fontforge.github.io/pfaeditmath.html last updated 7/27/2017
Frequently Asked Questions http://fontforge.github.io/faq.html last updated 7/27/2017
Glossary of (some) typographical terms http://fontforge.github.io/glossary.html last updated 7/27/2017
High level description of what each source file contains… http://fontforge.github.io/src.html last updated 7/27/2017
Hot Keys http://fontforge.github.io/HotKeys.html last updated 7/27/2017
Importing a glyph designed in some other vector editor http://fontforge.github.io/importexample.html last updated 7/27/2017
Index http://fontforge.github.io/realindex.html last updated 7/27/2017
License and Copyright http://fontforge.github.io/license.html last updated 7/27/2017
More advanced features, ligatures, mark positioning, glyph variants http://fontforge.github.io/editexample6.html last updated 7/27/2017
Outline Glyph View http://fontforge.github.io/charview.html last updated 7/27/2017
Plugins in FontForge http://fontforge.github.io/plugins.html last updated 7/27/2017
sfddiff -- A program for comparing fonts http://fontforge.github.io/sfddiff.html last updated 7/27/2017
Special thoughts for special scripts http://fontforge.github.io/scriptnotes.html last updated 7/27/2017
Spline Font Database File Format http://fontforge.github.io/sfdformat.html last updated 7/27/2017
Steps to creating a font… http://fontforge.github.io/editexample.html last updated 7/26/2017
The File Menu http://fontforge.github.io/filemenu.html last updated 7/27/2017
The Font View http://fontforge.github.io/fontview.html last updated 7/27/2017
The Metrics View http://fontforge.github.io/metricsview.html last updated 7/27/2017
Unicode Corporate Characters used by FontForge http://fontforge.github.io/corpchar.html last updated 7/27/2017
User Interface Translation Notes http://fontforge.github.io/uitranslationnotes.html last updated 7/27/2017
Using FontForge with TeX http://fontforge.github.io/PfaEdit-TeX.html last updated 7/27/2017
Writing python scripts to change fonts in FontForge http://fontforge.github.io/python.html last updated 7/27/2017
Writing scripts to change fonts in FontForge http://fontforge.github.io/scripting.html last updated 7/27/2017
X Resources http://fontforge.github.io/xres.html last updated 7/27/2017

Link of Related Download

Download FontForge http://fontforge.github.io/en-US/downloads/ last updated 7/22/2017

The FontForge can be downloaded at
http://downloads.sourceforge.net/project/fontforge/fontforge-executables/FontForgeSetup_2012-07-31_Windows.exe (setup version)
http://sourceforge.net/projects/fontforge/files/fontforge-executables/FontForge_2012-07-31_Windows.7z/download (exe version)

OCT 2012

S	M	T	W	T	F	S

	1	2	3	4	5	6
7	8	9	10	11	12	13
14	15	16	17	18	19	20
21	22	23	24	25	26	27
28	29	30	31

FEB 2011

S	M	T	W	T	F	S

		1	2	3	4	5
6	7	8	9	10	11	12
13	14	15	16	17	18	19
20	21	22	23	24	25	26
27	28

Sideway BICK Blog

16/10