 Sideway
BICK BLOG from Sideway
Sideway
BICK BLOG from Sideway
|
Link:http://output.to/sideway/default.asp?qno=121100002 Moment of Inertia of Mass, Moment inertia of Thin Plate Second Moment of MassSimilarly, the second moment of mass about an axis is equal to the summation of the products of the square of the distance between the elemental mass and the reference axis, and the elemental mass over an area. As the second moment of mass is usually refered to the rotation, the distance between the elemental mass and the rotating axis is denoted by r. Imply 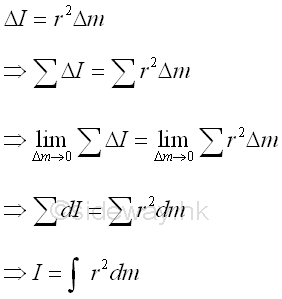
Moment of Inertia of a Thin Plate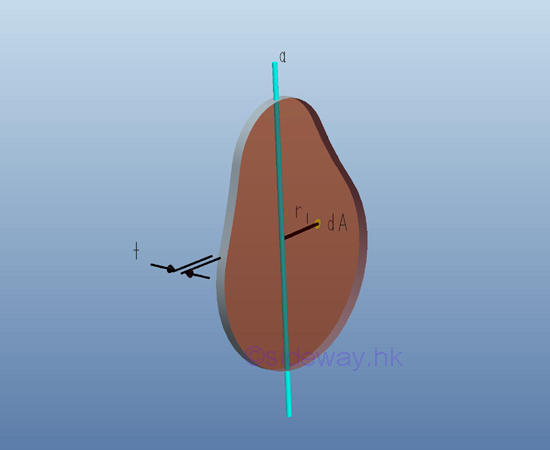
Consider a thin plate of area A with uniform thickness t and homogenouse material density ρ. Both the thickness and the material density are constant over the area. Since the thickness t is much smaller than the plate dimension, the mass and the elemental mass of the thin plate can be expressed in terms of the thickness and the material density, if the reference axis lies in the middle plane of the plate, the mass moment of inertia of the thin plate with respect to an axis can be expressed as the elemental area on the middle plane with the distance r as the radius between the elemental area and the axis. Imply 
Therefore for a uniform homogenous thin plate, the mass moment of inertia about axis a can be expressed in terms of area moment of inertia about axis a. Imply 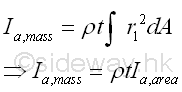
For the mass moment of inertia about axis b, which is perpendicular to axis a. 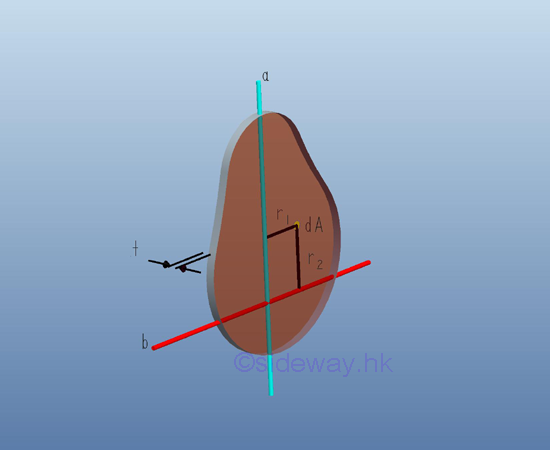
Similarly, the mass moment of inertia about axis b, which is perpendicular to axis a can be expressed in terms of the area moment of inertia about b as in the rectangular moments of inertia. Imply 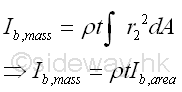
And for the mass moment of inertia about axis c, which is perpendicular to the plate and pass through the intersection of axes a and b. 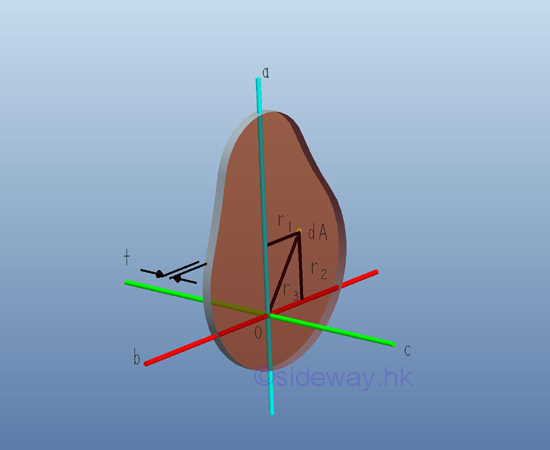
Similarly, the mass moment of inertia about axis c, which is perpendicular to the plate and pass through the intersection of axes a and b can be expressed in term of the area polar moment of inertia about pole O in magnitude but the mass moment of inertia is concerning about the inertia of rotation about the axis c. Imply 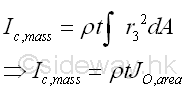
Therefore, from the relation between the rectangular area moments of inertia and the polar area moment of inertia, the relationship for the rectangular mass moments of inertia of a unform homogenous thin plate is 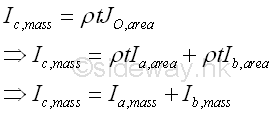
Moment of Inertia of Thin Circular Plate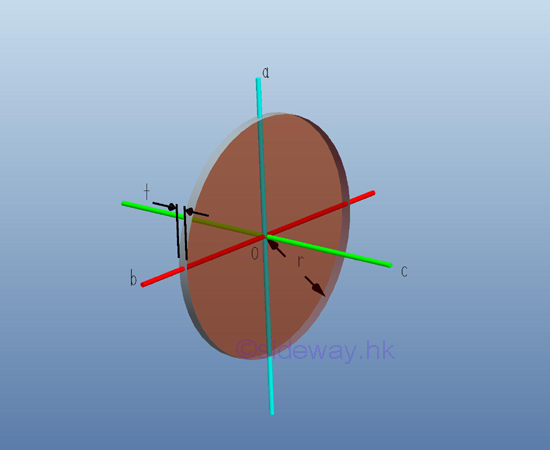
For a thin uniform homogenous circular plate, the mass moment of inertia about the rectangular coordinate axes, a and b, passing through the centre of gravity of the circular plate can be obtained from the area moment of inertia. Imply 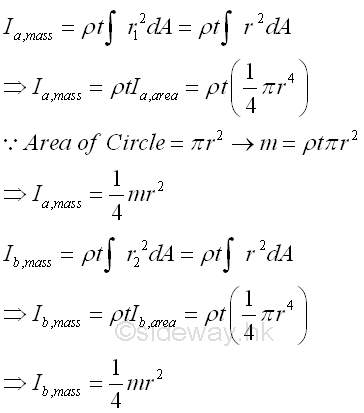
Similarly, the mass moment of inertia about axis c perpendicular to the rectangular coordinate axes a and b can also be obtained from the relation between the polar area moment of inertia and the rectangular area moment of inertia. Imply 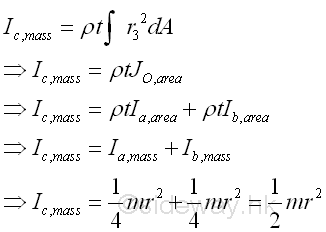
Moment of Inertia of Thin Rectangular Plate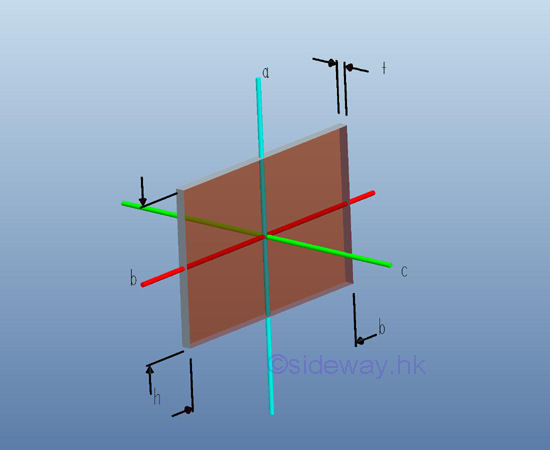
For a thin uniform homogenous rectangular plate, the mass moment of inertia about the rectangular coordinate axes, a and b, passing through the centre of gravity of the circular plate can be obtained from the area moment of inertia. Imply 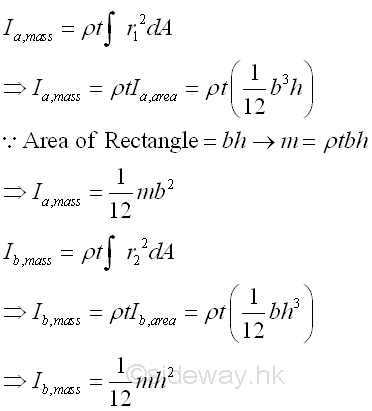
Similarly, the mass moment of inertia about axis c perpendicular to the rectangular coordinate axes a and b can also be obtained from the relation between the polar area moment of inertia and the rectangular area moment of inertia. Imply 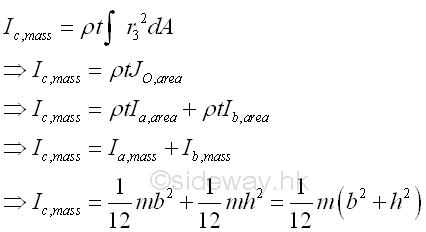
Link:http://output.to/sideway/default.asp?qno=121000002 Moment of Inertia of an Area Second Moment of An Area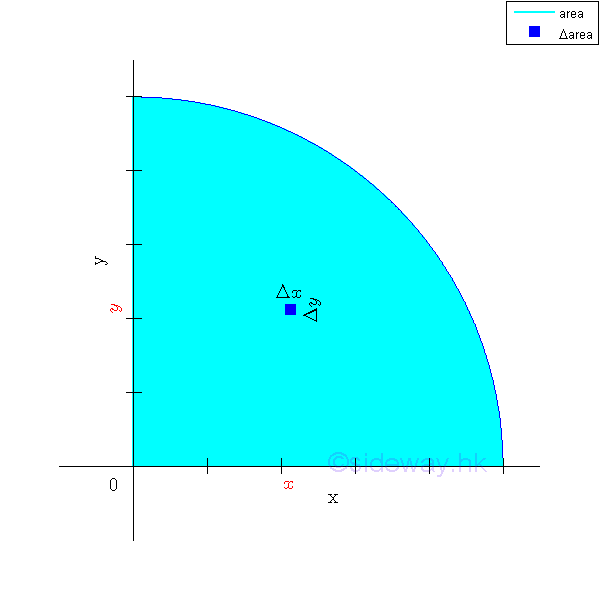
By definition, second moment of an area about an axis is equal to the summation of the products of the square of the distance between the elemental area and the reference axis, and the elemental area over an area. Rectangular Moment of Inertia of an AreaThe two most common second moments are the rectangular moments of inertia of an area about the two coordinate axes. Imply 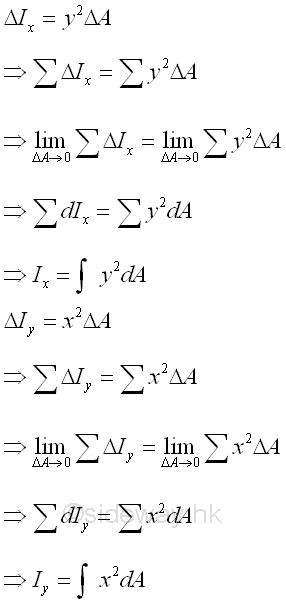
The elemental differential area is defined as a second order element of dxdy. And a double integration is needed to determine the second moment of an area. 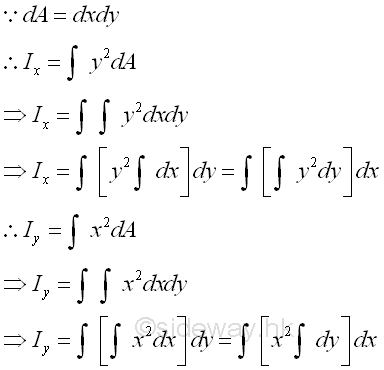
However, when a group of second order elements can be grouped into a first order element, the elemental differental area can then be expressed as a first order element e.g. a rectangular strip. Only a single integration is needed to determine the second moment of an area. Elemental Horizontal Strip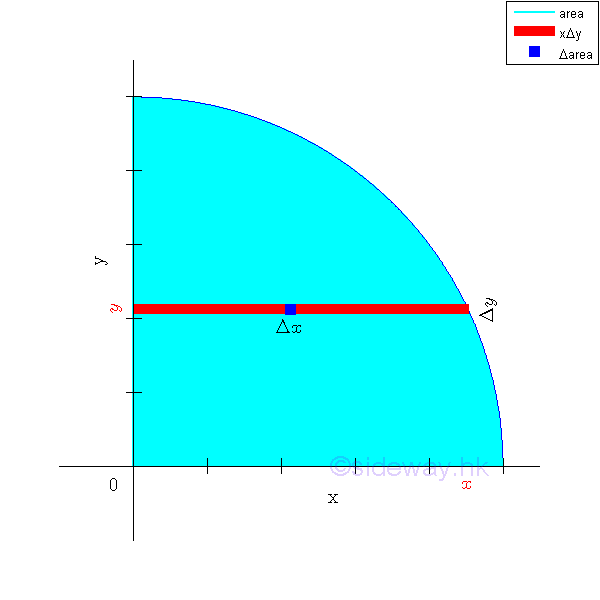
When the second order element areas can be grouped as a first order element, e.g. a horizontal rectangular strip by neglecting the higher order term, only a single integration is needed to determine the second moment of an area. Since the elemental area of a horizontal strip have the same distance from the x-axis. Imply 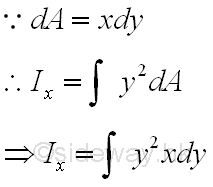
Elemental Vertical Strip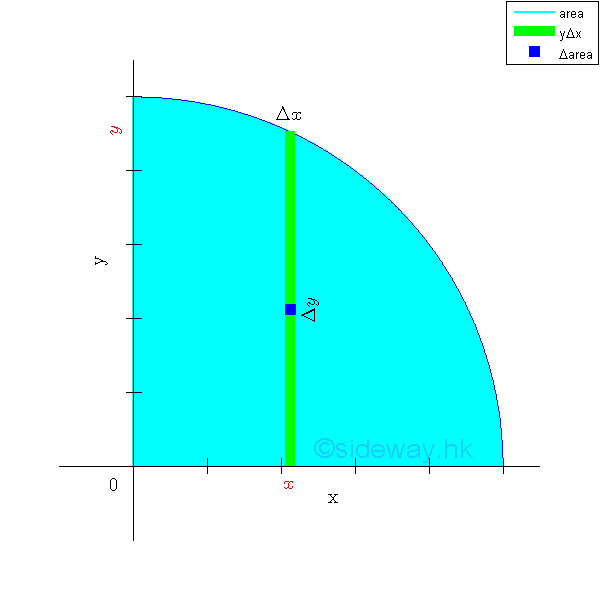
When the second order element areas can be grouped as a first order element, e.g. a vertical rectangular strip by neglecting the higher order term, only a single integration is needed to determine the second moment of an area. Since the elemental area of a vertical strip have the same distance from the y-axis. Imply 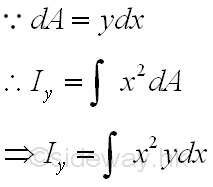
Elemental Rectangular Strip about the referenc axis perpendicular to the lengthBecause of the distance between the reference axis and elemental area of the rectangular strip is not a constant when the reference axis is not parallel to the lenght of the elemental rectangular strip, the second order differential area element cannot be replaced by the first order differential area element directly. However, the second order differential area element can be replaced by the first order differential area element, if the distance can be expressed as the function along the reference axis or the length of the elemental rectangular strip. For a horizontal elemental rectangular strip, the second moment about an vertical axis is 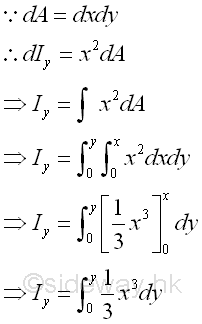
For a vertical elemental rectangular strip, the second moment about an horizontal axis is 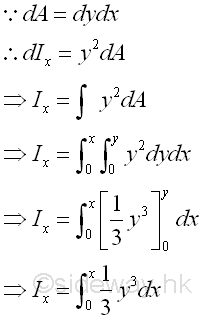
Polar Moment of Inertia of an Area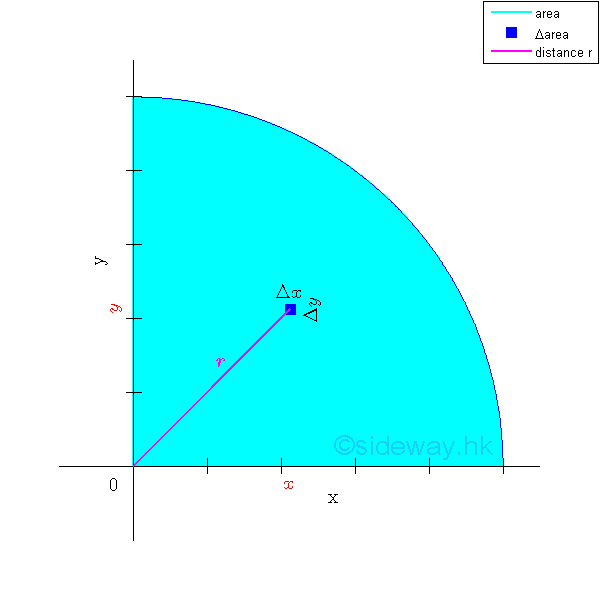
Besides the rectangular moments of inertia, another important second moment of an area is the polar moment of inertia, which is the second moment of an area about the axis normal to the planar area. And usually the polar moment of inertia of the area is defined with respect to the z axis or the pole at the origin O. Imply 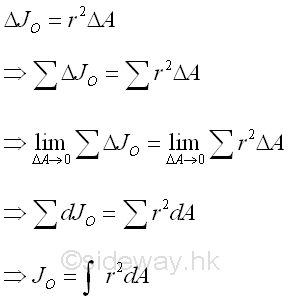
By considering the same second order differential area element, the polar moment of inertia of the area can be determined from the rectangular moments of inertia, Ix and Iy if the two rectangular moments of inertia are known using the perpendicular axis theorem. Imply 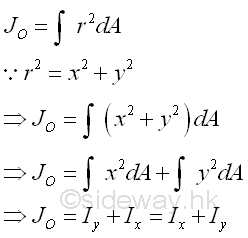
If the bounding profile of the area is expressed in form of polar coordinates, the polar moment of inertia about the pole can also be determined by the second moment of an area with the second order differential polar area element. Imply 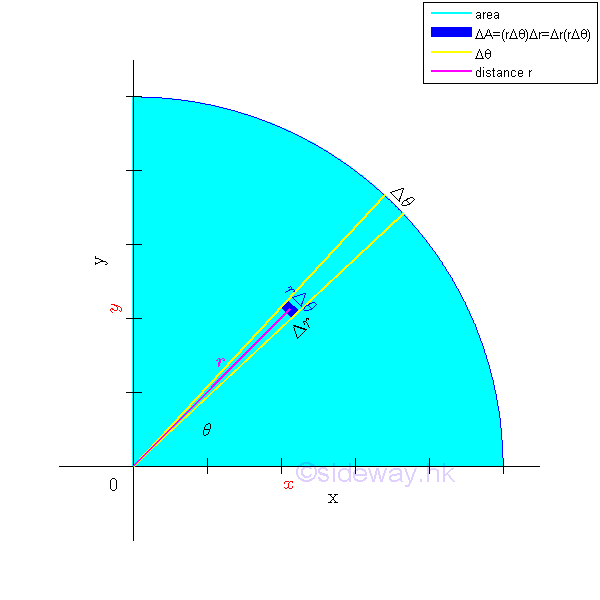
Imply 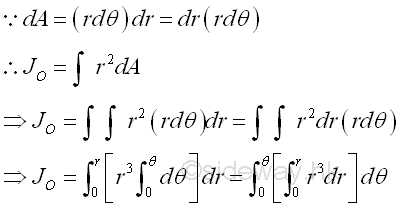
Or the polar moment of inertia about the pole can be determined by the second moment of an area with the first order differential polar area element. Elemental Arc Strip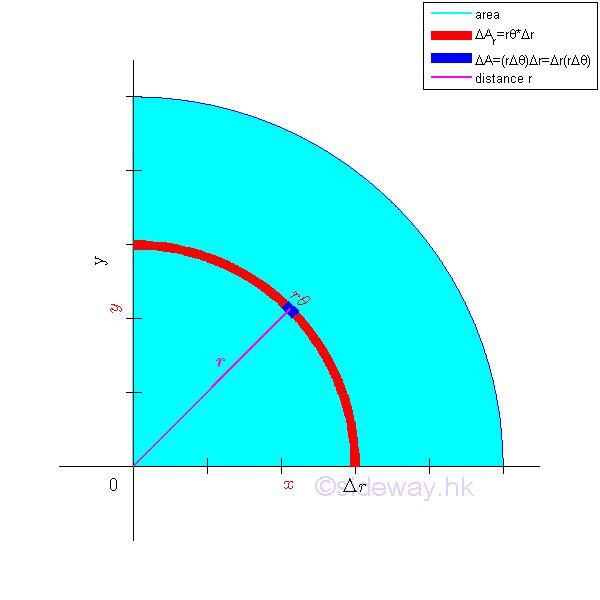
The polar moment of inertia about the pole can be determined by the second moment of an area with the first order differential elemental arc strip. Since the distance between the differential elemental area and the pole is the same. Imply 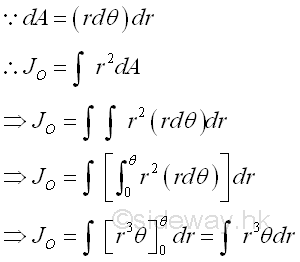
Elemental Sector Slice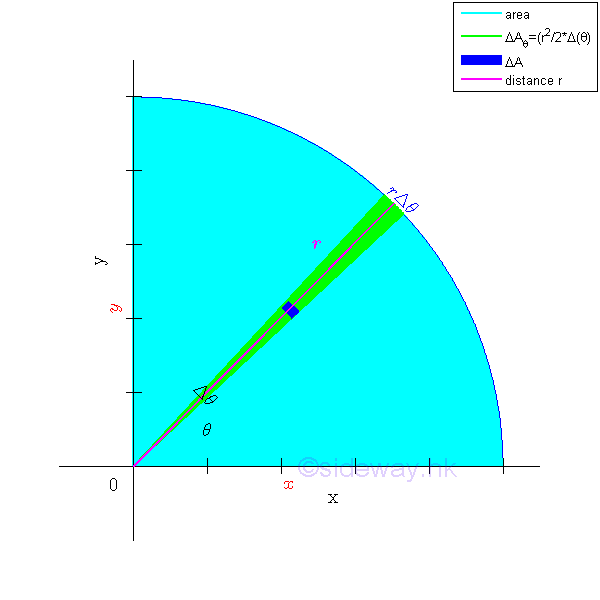
The polar moment of inertia about the pole can be determined by the second moment of an area with the first order differential elemental sector slice. Since the distance between the reference axis and elemental area of the sector slice is not a constant, the second order differential area element cannot be replaced by the first order differential area element directly. However, the second order differential area element can be replaced by the first order differential area element, if the distance can be expressed as the function along the reference pole or the radius of the elemental sector slice. For an elemental sector slice, the second moment about the pole is 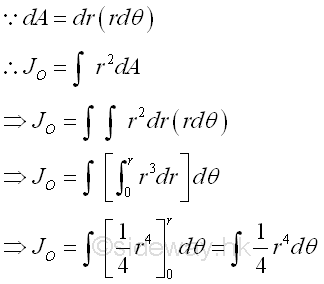
Second Moment and First Moment of an AreaThe value of first moment can be positive, negative and zero. But the second moment is always positive because the area element is alway positive, and the square of the distance is also alway positive. And therefore both the rectangular moment of inertia and the polar moment of inertia must be positive regardless of the location of the area element locating on the coordinate system. Besides, the dimension of second moment of an area is of length to the fourth power, while the first moment of an area had dimensions of length to the third power. Radius of Gyration of an Area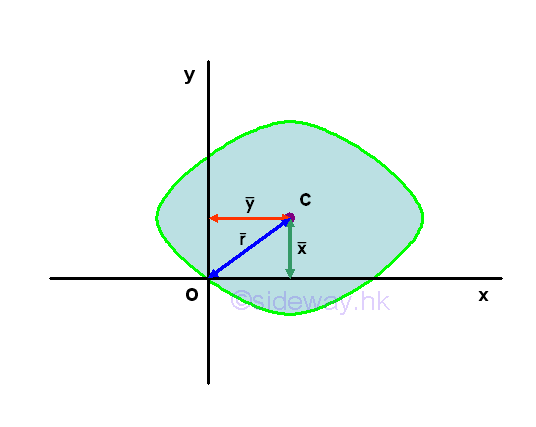
For an area, the first moment of the area about an axis or a point can be expressed as product of the imaginary total area of the area at the centroid of the area and the shortest distance between the centroid of the area and the reference axis or the reference point. But for the second moment of the area, there is only an distance, called the radius of gyration, i.e. kx or ky, to describe the distance between the location of an imaginary total area strip of the area and the reference axis or pole such that an equivalent second moment of the area is created by assuming the imaginary total area of the area is placed at this distance away from the reference axis. Or similarly the polar radius of gyration, kO about the pole. Imply 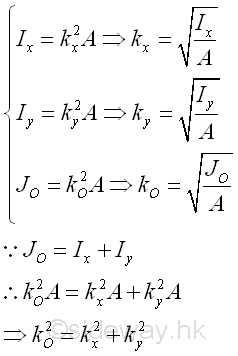
Imply 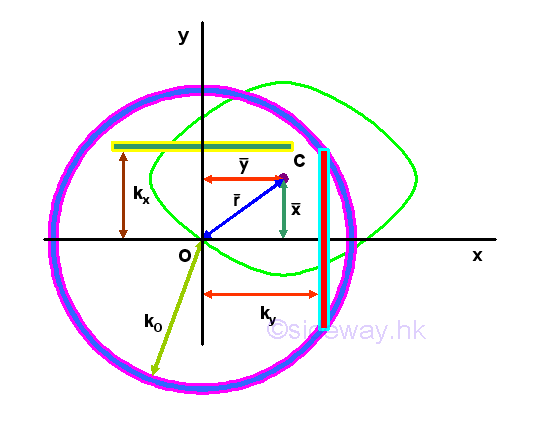
Parallel-Axis Theorem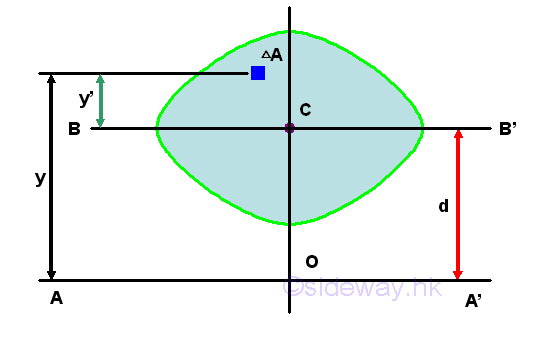
Unlike the first moment about the axis passing through the centroid, i,.e. the centroidal axis, the second moment about the axis, BB' passing through the centroid is not equal to zero. And the second moment of an area, A about the axis passing through its centroid is called the centroidal moment of inertia I of the area. Imply 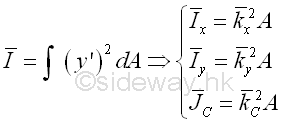
Consider the moment of inertia I of the area A about the axis, AA'. Imply 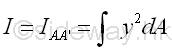
The distance y in the integral can be expressed in terms of the distances y' and d. Imply 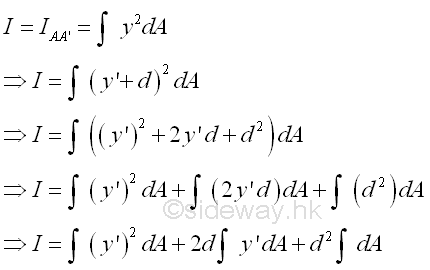
The integral of the moment of inertia I of the area A about the axis, AA' can be divided into three seperated integrals. The first integral is the centroidal moment of inertia I of the area. The second integral is the first moment of the area A about the centroidal axis and the value of the first moment of the area about the centroidal axis is equal to zero. The third integral is equal to the total area only. The square of the distance d is alway positive also, therefore the third term is alway positive regardless of the location of the parallel reference axis. Imply 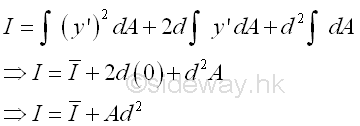
Therefore the second moment of an area A about an axis AA' is equal to the second moment of an area A about the centroidal axis BB' parallel to the reference axis AA' plus the product of the area A and the square of the distance d between the two parallel axes. This is called the parallel-axis theorem. Similarly, the theorem can also be applied to the polar moment of inertia about a pole O. Imply 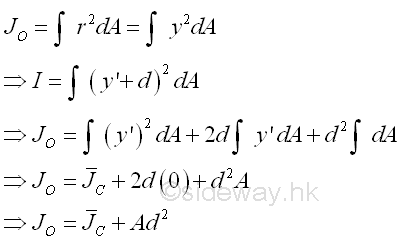
The theorem can also be expressed in terms of the radius of gyration of an area. Imply 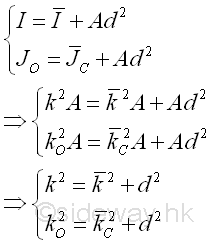
Since the theorem can only be used to relate the second moment of an area about an axis with the second moment of an area about the centroidal axis parallel to the reference axis, two second moments of an area about two parallel axes can not be transferred directly. e.g. 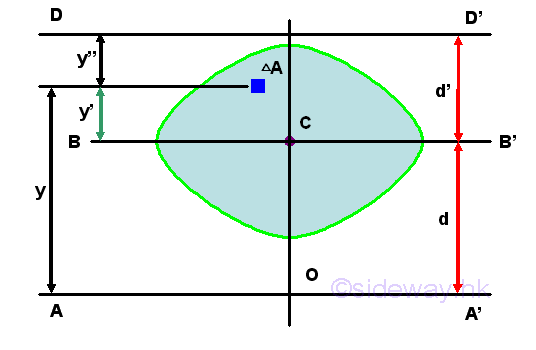
Imply 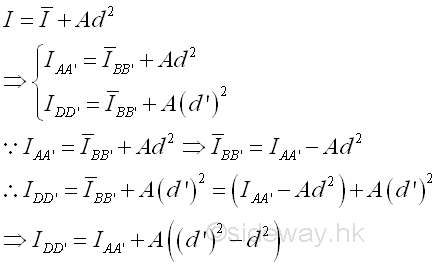
Link:http://output.to/sideway/default.asp?qno=121000001 Moment of Inertia Second MomentMoment is the concept of a concentrated force about a point and is proportional to the distance between the force and the reference point. In general, the first moment of a body about a reference is the summation of the moment of uniformly distributed forces over the body relating to the first order of distance and the shape of the body only. Although, the moment of distributed forces of intensity proportional to the distance between the force and the reference is also proportional to the distance between the force and the reference, the summation of the moment of the distributed forces of intensity proportional to the distance over the body relating to the square of the distance or the second order of distance and the shape of the body. Since these are common terms found in practical calculation, they are defined as the property of a body and is called the second moment of a body. For example, force acting on submerged plane surface can be expressed in terms of the differential elemental area, ΔA and the pressure, a function of the depth y, acting on the element. Imply 
Since the elemental force or the distributed forces is a function the depth y, the resultant force F can be determined by making use of the first moment of the body. Similarly, since the elemental moment of the distruibuted forces about a reference is a function of the square of the depth y, the resultant moment M can be determined by making use of the second moment of the body. And the point of application y of the resultant force F can be determined through system of forces transformation by equating the moment of the two system of forces. Imply 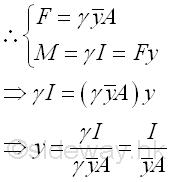
Moment of InertiaThe second moment of an area is also called moment of inertia or area moment of inertia. Besides, the application of fluid pressure of nonhorizontal submerged plane surface, second moment of an area is also involved in many engineering application analysis, e.g. bending stress, shearing stress, torsional shearing stress, angle of twist, buckling of a column, the area moment of inertia is usually refered to an plane area about an axis either parallel or normal to the plane area as the property of an plane area. Moment of inertia is commonly used for both areas and masses. The second moment of a mass is usually used to measure a body of mass to resist changes in rotational acceleration about an axis. The tendency to resist changes in their state of motion is called as inertia. The tendency to resist rotational acceleration obtained by the second moment of a mass is therefore called the moment of inertia of the body mass about the axis or the mass moment of inertia or moment of inertia. |
Sideway BICK Blog 07/10 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

