Kinetics: Impact

By the concept of impulse, the momentum change of an object over a very short time interval can be expressed in form of an impulsive force. Impact is another concept developed, in a more general sense, to study the motion of two objects coming in contact with each other and the effect of the collision under large impulsive forces between two objects over a small time interval.  

Impact and Momentum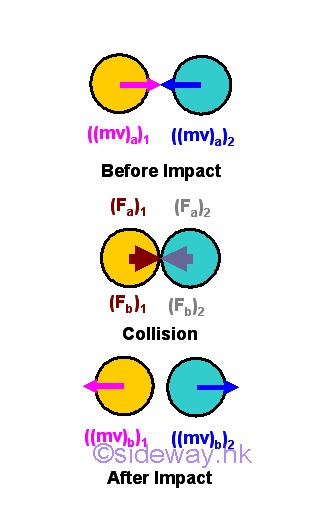

In general, the concept of an impulse is a force acting on an object over a very short time interval, while the concept of an impact is an object collides with another object over a very short time interval. From the concept of impulse, momentum of an moving object can be transformed into impulse to act on another object. By making use of the impulsive force concept, the two produced impulsive forces act simultaneously on both objects respectively during the time of collision. During the collision period, the resultant impact force will cause the two objects to move together in the direction of the resultant force. And at the end of collision, the motion of each object can then be obtained by the principle of impulse and momentum together with the produced impulsive force acting upon the corresponding object. And the concept of impact is usually applied to the collision between two objects during which large impulsive forces are produced on each other relatively over a very small time interval. When considering the two object as one single system, the total momentum of two objects must be conserved as there is no external impulsive force.

Types of Impact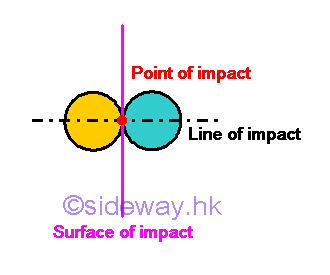

When two objects collide at a point of contact, there always exists a straight line normal to the surface of contact in contact during the impact if the friction force between two objects is neglected. The straight line is called line of impact. For particle objects, the impact is always a central impact because mass centers of the two colliding objects are always passing through the line of impact. But the type of central impact can further be divided into two categories according to the direction of the object motion with respect to the line of impact.

A direct central impact is an impact in which the motions of both two objects are along with the line of impact without considering the direction of the motion.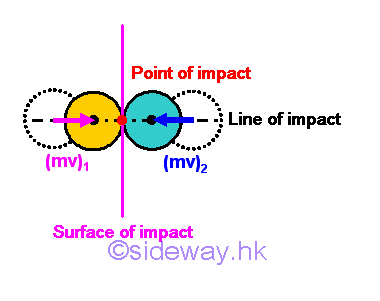 

A oblique central impact is an impact in which at least one of the motions of both two objects are not along with the line of impact without considering the direction of the motion. Therefore direct central impact is only a special case of oblique central impact.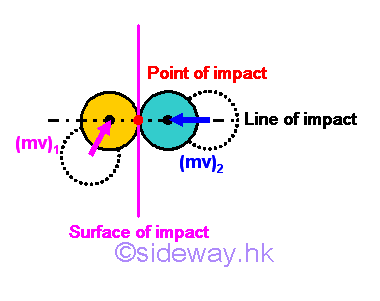

But for body objects, only the impact with both mass centers of the two colliding body objects passign through the line of impact is a central impact.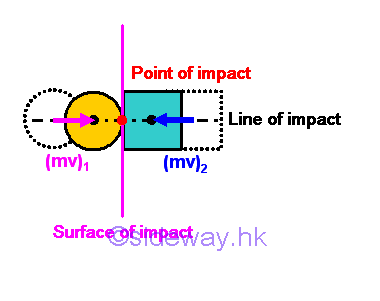

For those impact with at least one mass center that is not located on the line of impact is called eccentrc impact in which angular momentum is always involved. And therefore for the case of body objects, motion of both body objects should not produce angular momentums that can not be neglected, even in the case of oblique central impact of body objects, in order to formulating the impact as a central impact problem without considering the angular momentums of body objects.  

Direct Central Impact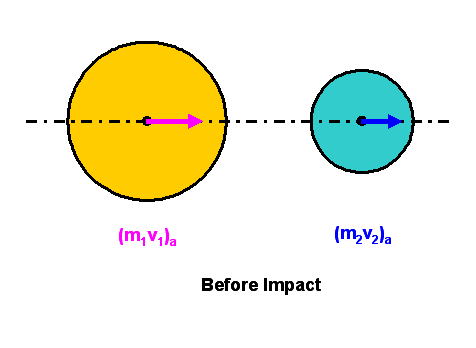

To simplify the study of a direct central impact, assuming two objects 1 and 2, move along with a straight line in the same direction at a distance apart. If object 1 follows object 2 and moves at a higher velocity than object 2, object 1 will collide with object 2 eventually. Assuming object 1 is also heavier than object 2, the momentum of object 1 must therefore larger than object 2 also.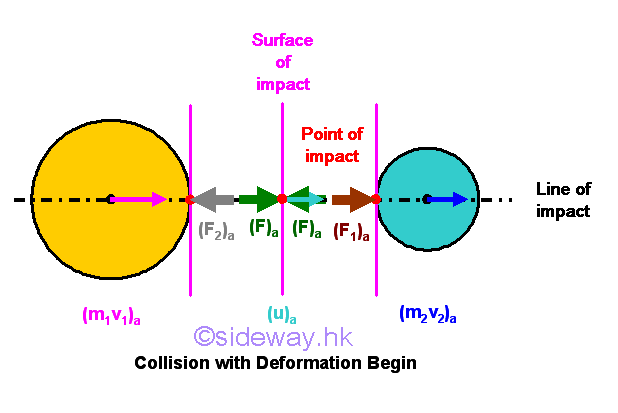

In a simplified approach, the momentums of objects are transformed into impulses acting on each other during an impact. By Newton's first law, forces are produced when objects 1 and 2 collide in order to cause the changing of the motions of objects 1 and 2. By Newton's third law, generated action and reaction forces are always equal and opposite, that is for an impulsive force produced by an initiated object acting on another object, there always exists a reaction impulsive force produced by another object to react the the initiated object also. Therefore the impulsive force acting upon the two objects 1 and 2 at the point of impact must be equal and opposite, and along the line of impact also. During the collision of an impact, both objects 1 and 2 move together, but the velocities of the both objects 1 and 2 with respect to the mass centers of both objects 1 and 2 may not be at the same velocity because of the structure or material deformations of objects 1 and 2 caused by their momentums and  reaction forces acting on them. Only the velocities of both objects 1 and 2 at the point of impact are the same . In other words, the impulsive forces at the point of impact need time to ramp up to the maximum therotical impulsive forces between two objects 1 and 2.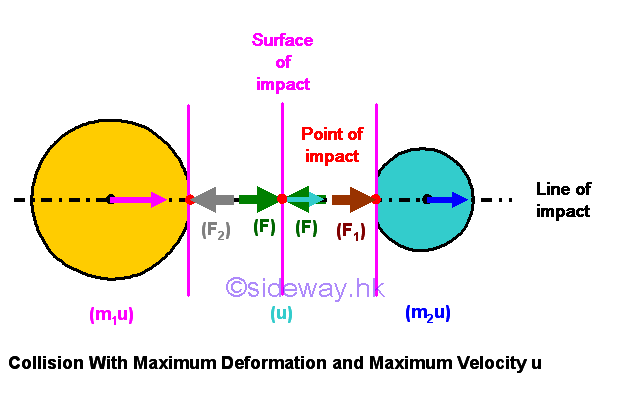

As the collision continued, the accumulated impulsive force acting upon the two objects 1 and 2 at the point of impact increase simultaneously, and the velocity at the point of impact and mass centers of objects 1 and 2 change accordingly by the Newton's second law. The structural or material deformations of objects 1 and 2 caused by their momentums and  reaction forces acting on them will be continued also. In a general sense, object 1 with higher velocity is slowed down by the impulsive force at the point of impact and object 2 with lower velocity is speeded up by the impulsive force at the point of impact during the collision of impact. Since the impulsive force is caused by the difference in the motion of objects 1 and 2, the impulse produced by objects 1 and 2 at the point of impact will act upon each other simultaneously by the principle of impulse and momentum through the impulsive force at the point of impact  by Newton's law of motion until the velocities of both objects 1 and 2 with respect to the mass centers of object 1 and 2 have the same velocity as the velocity at the point of impact. In both case, by the principle of impulse and momentum, the two objects are in dynamic equilibrium and the total momentum of the system is conserved when there is no external force.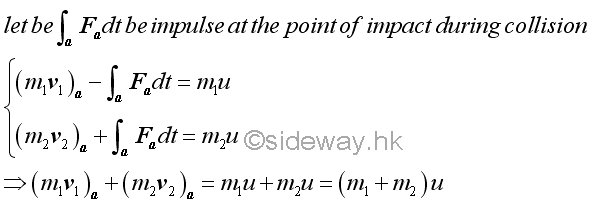

The two objects move independingly at an instant of time. Since there is no more momentum change to continue the collision, the restitution of the objects occur.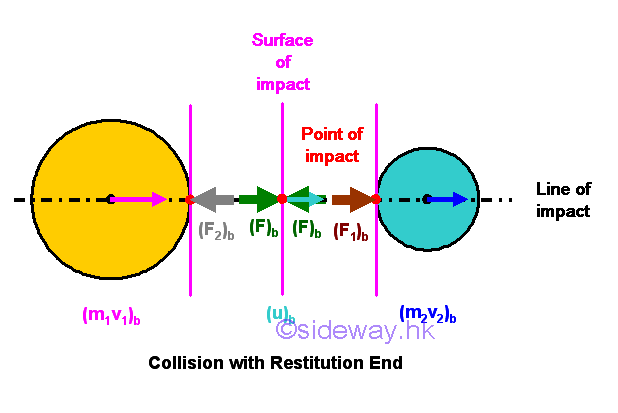

The restitution is caused by the restoration of the deformated object causes by the accumulated impulsive force at the point of impact.

The accumulated restoration impulsive force acting on each other is then transformed into moment change accordingly during the restitution period.

The two objects continue their motions independingly.

Conservation of Total Momentum

The two objects move independently after the impact. When considering the two objects as one single system. the total momentum of the two objects is convserved.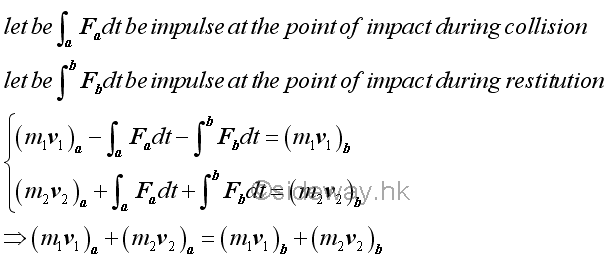

Coefficient of Restitution

When an object impacts with another object, two objects first collides together and the collision period is associated with the mechanical deformation of the objects. And after the instant of maximum deformation, the two objects restitute to move independently and the restitution period is associated with the mechanical restoration of the objects. In general, the accumulated impulsive force exerted at the point of impact during the restitution period may differ from the accumulated impulsive force exerted at the point of impact during the collision period. Usually the accumulated impulsive forces produced from the restoration of the objects are smaller than the accumulated impulsive forces used to form the deformation of the objects. The ratio of the magnitudes of impulses for two specified colliding objects corresponding to the restoration period and the deformation period respectively is called the coefficient of restitution, denoted by e. 

The coefficient of restitution depends highly on the material of the two colliding objects. But the coefficient of restitution is also affected by the impact velocity, the shape and size of the two colliding objects. Since the masses of the two colliding objects are constants, the coefficient of restitution can also be expressed in terms of the ratio of the relative velocity of the two objects after the impact and the relative velocity of the two objects before the impact. Or the relative velocity of the two objects after the impact is equal to the coefficient of restitution times the relative velocity of the two objects befor the impact.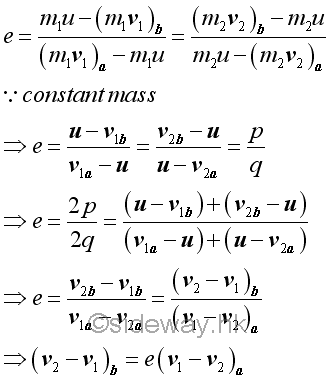

Equations of Impact

By the principle of the conservation of momentum, the total momentum of the system of two objects is conserved during the collision of an impact since there is no external force acting on the system of two objects. Besides, the relative motion of the two objects can be related by the coefficient of restitution e using the principle of impulse and momentum with respect to the momentum change or relative motion of the objects. Therefore the velocities of the two objects can be determined by solving the two equations simultaneously.

Perfectly Plastic Impact

When the coefficient of restitution e is equal to zero, the impact is called perfectly plastic impact. By the definition of the coefficient of restitution, the impulses received by both objects during the period of restitution are equal to zero. In other words, the relative velocity of two objects after impact is equal zero and therefore the velocities of the two objects are the same.As there is no period of restitution, both particles move at same velocity together after impact. Since the total momentum of a system is conserved, the common velocity of both objects can be determined from the total momentum equation of the system directly.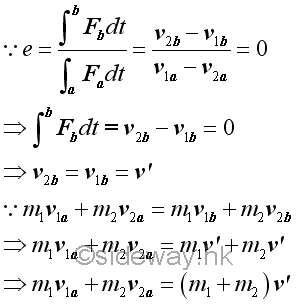

Perfectly Elastic Impact

When the coefficient of restitution e is equal to one, the impact is called perfectly elastic impact.  By the definition of the coefficient of restitution, the impulses received by both objects during the period of deformation and the period of restitution are equal. The relative velocity of two objects after impact is equal to the relative velocity of two objects before impact. Or the momentum change of two objects after impact is equal to the momentum change of two objects before impact. Since the total momentum of a system is conserved, the velocities of both objects can be determined by solving the equation of coefficient of restitution with respect to the momentum change and the total momentum equation of the system simultaneously.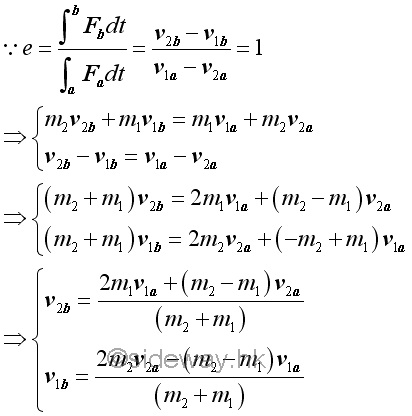   

When the coefficient of restitution is equal to one, the total kinetic energy of two objects before the impact is also equal to the total kinetic energy of the two objects after impact. That is the kinetic energy of the system of two objects is conserved.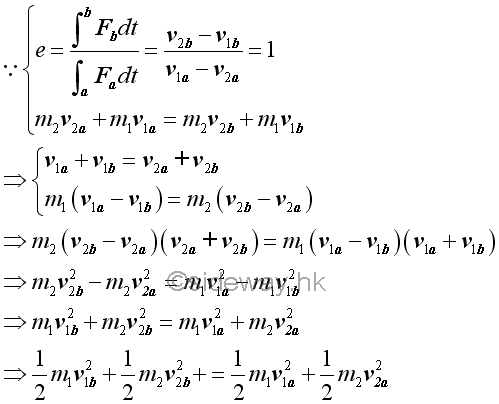  

Oblique Central Impact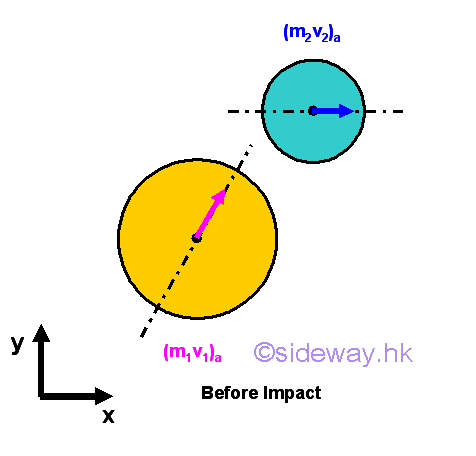

Assuming two objects 1 and 2 move with a constant velocity in different direction at a distance apart. If object 1 moves at a higher velocity than object 2 such that object 1 will collide with object 2 eventually. Assuming object 1 is also heavier than object 2, the momentum of object 1 must therefore larger than object 2 also.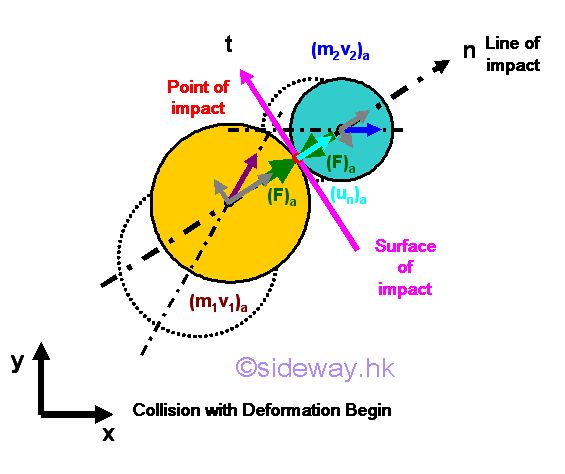

Similar to direct central impact, the momentums of objects are transformed into impulses acting on each other during an impact. The generated action and reaction impulses at the point of impact are always equal and opposite along the line of impact. By assuming the contact surfaces of the two objects are perfectly smooth and frictionless, the impulsive force component tangent to the surface of impact is eqaul to zero and the impulsive force component along with the line of impact are always normal to the surface of impact. Since the two objects collides over a very short time interval only, the motions of two objects along with the line of impact can be assumed to be always normal to the surface of impact and passing the mass centers of two objects such that the impulses can be resolved into normal component with respect to the surface of impact only. By resolving the motion of objects 1 and 2 into normal and tangential components with respect to the surface of impact, the period of deformation due to normal components of the motions is also similar to that of the direct central impact. During the collision of an impact, both objects 1 and 2 move together, but the velocities of the both objects 1 and 2 with respect to the mass centers of both objects 1 and 2 may not be at the same velocity because of the structure or material deformations of objects 1 and 2 caused by their momentums and  reaction forces acting on them. Only the velocities of both objects 1 and 2 at the point of impact are the same. In other words, the impulsive forces at the point of impact need time to ramp up to the maximum therotical impulsive forces between two objects 1 and 2. As there is no tangential impulsive force, the tangential components of the motions of objects 1 and 2 remain unchange during the impact.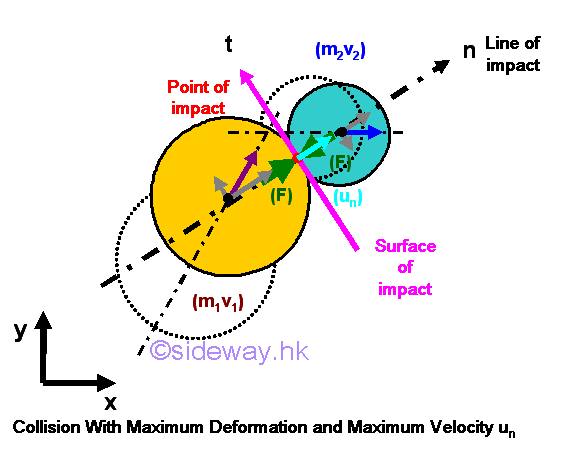

By resolving the motions of two objects in normal and tangential components, the tangential motions of the two objects move free during the period of deformation in the collision and the normal motions of the two objects are affected by the deformations of the objects during the collision. As the collision continued, the accumulated impulsive force acting upon the two objects 1 and 2 at the point of impact increase simultaneously, and the velocity at the point of impact and mass centers of objects 1 and 2 change accordingly by the Newton's second law. The structural or material deformations of objects 1 and 2 caused by their momentums and  reaction forces acting on them will be continued also. In a general sense, object 1 with higher velocity is slowed down by the impulsive force at the point of impact and object 2 with lower velocity is speeded up by the impulsive force at the point of impact during the collision of impact. Since the impulsive force is caused by the difference in the motion of objects 1 and 2, the impulse produced by objects 1 and 2 at the point of impact will act upon each other simultaneously by the principle of impulse and momentum through the impulsive force at the point of impact  by Newton's law of motion until the velocities of both objects 1 and 2 with respect to the mass centers of object 1 and 2 have the same velocity as the velocity at the point of impact. In both case, by the principle of impulse and momentum, the two objects are in dynamic equilibrium and the total momentum of the system is conserved.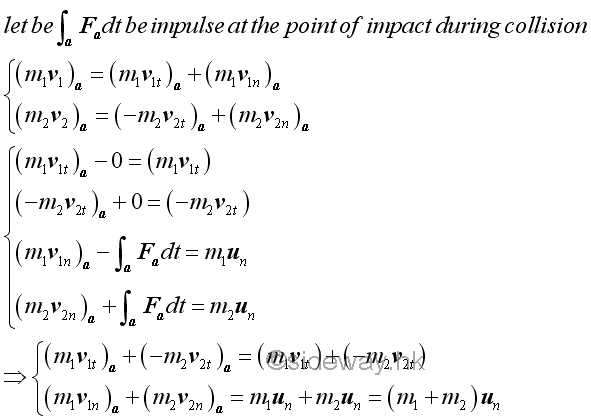

The two objects move independingly at an instant of time. Since there is no more momentum change to continue the collision, the restitution of the objects occur.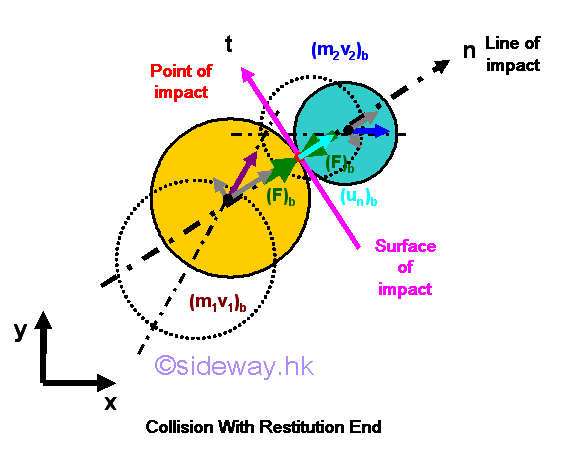

The restitution is caused by the restoration of the deformated object causes by the accumulated impulsive force at the point of impact.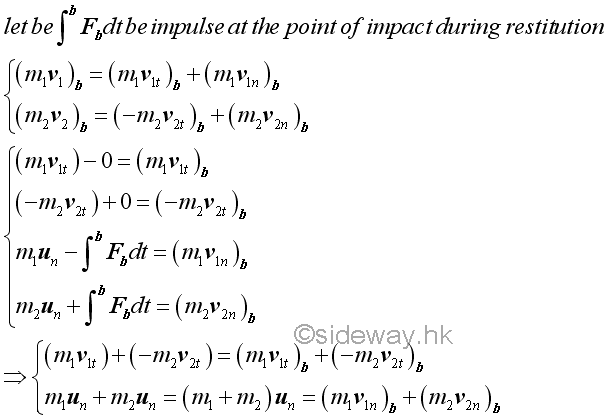

The accumulated restoration impulsive force acting on each other is then transformed into moment change accordingly during the restitution period.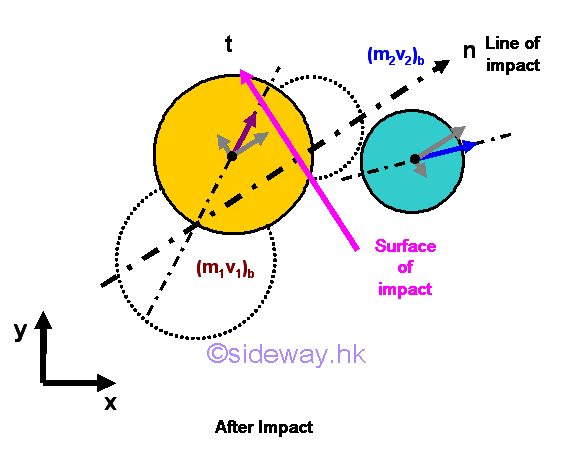

The two objects continue their motions independingly.

Conservation of Total Momentum

The two objects move independently after the impact. When considering the two objects as one single system. the total momentum of the two objects is convserved.

Coefficient of Restitution

When an object impacts with another object, two objects first collides together and the collision period is associated with the mechanical deformation of the objects. And after the instant of maximum deformation, the two objects restitute to move independently and the restitution period is associated with the mechanical restoration of the objects. In general, the accumulated impulsive force exerted at the point of impact during the restitution period may differ from the accumulated impulsive force exerted at the point of impact during the collision period. Usually the accumulated impulsive forces produced from the restoration of the objects are smaller than the accumulated impulsive forces used to form the deformation of the objects. The ratio of the magnitudes of impulses for two specified colliding objects corresponding to the restoration period and the deformation period respectively is called the coefficient of restitution, denoted by e. But for oblique central impact, the coefficient of restitution only associated with the normal components of the momentums.

The coefficient of restitution depends highly on the material of the two colliding objects. But the coefficient of restitution is also affected by the normal impact velocity, the shape and size of the two colliding objects. Since the masses of the two colliding objects are constants, the coefficient of restitution can also be expressed in terms of the ratio of the relative normal velocity of the two objects after the impact and the relative normal velocity of the two objects before the impact. Or the relative normal velocity of the two objects after the impact is equal to the coefficient of restitution times the relative normal velocity of the two objects befor the impact.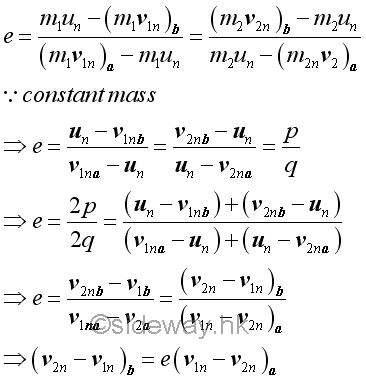

Equations of Impact

By the principle of the conservation of momentum, the normal momentum of the system of two objects is conserved during the collision of an impact since there is no external force acting on the system of two objects. Besides, the relative normal motion of the two objects can be related by the coefficient of restitution e using the principle of impulse and momentum with respect to the momentum change or relative motion of the objects. Therefore the normal velocities of the two objects can be determined by solving the two equations simultaneously. And equations of impact can be obtained accordingly.