 Sideway
BICK BLOG from Sideway
Sideway
BICK BLOG from Sideway
|
Link:http://output.to/sideway/default.asp?qno=120700003 Centroid of 3D Body Theorems of Pappus-GuldinusThe theorems of Pappus-Guldinus were formulated by the Greek geometer Pappus of Alexandria during the 4th century A.D. (about 340 A.D.) and were restated by the Swiss mathematician Paul Guldinus (1640). The two theorems of Pappus-Guldinus describe the area of surface of revolution and the volume of body of revolution by the circular path traversed by their centroid during the revolution. Theorem 1: Surface of RevolutionFor the surface of a surface of revolution generated by the rotation of a plane curve about a non-intersecting axis, the surface area A of the surface of revolution is equal to the product of the curve length L of the generating curve and the travelled distance d of the centroid of the generating curve during the generation of the surface by revolution. And the travelled distance of the centroid by revolution can also be expressed in terms of the perpendicular distance y of the centroid away from the rotating axis. 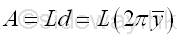
Surface of Revolution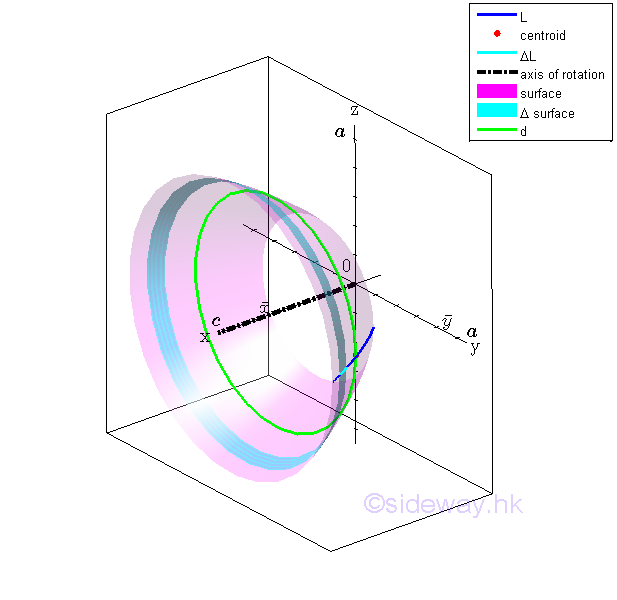
The area A of the surface of revolution can be determined by integration through the revolution of an elemental segment dL. Imply 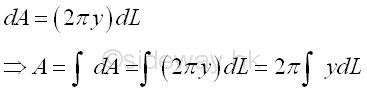
The area A can be rearranged in the form of the integral of the first moment of an elemental segment , which can also be expressed in terms of the centrod of the generating curve, Imply 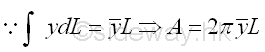
Theorem 2: Body of RevolutionFor the body of a body of revolution generated by the rotation of a plane region about a non-intersecting axis, the body volume V of the body of revolution is equal to the product of the area A of the generating plane region and the travelled distance d of the centroid of the generating region during the generation of the body by revolution. And the travelled distance of the centroid by revolution can also be expressed in terms of the perpendicular distance y of the centroid away from the rotating axis. 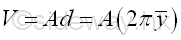
Body of Revolution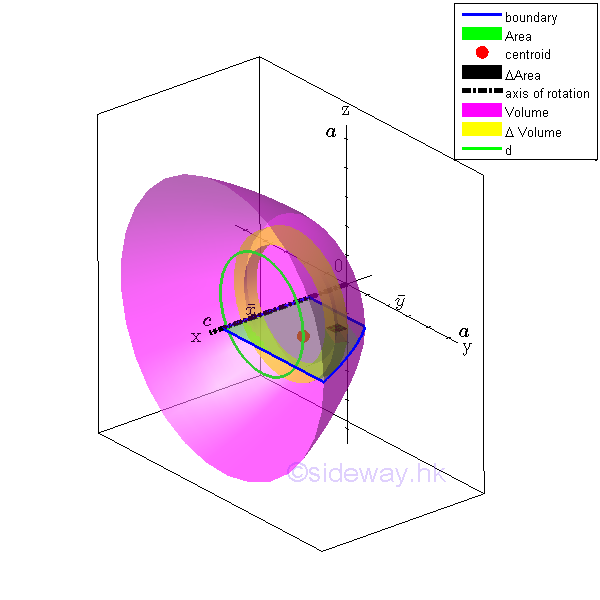
The volume V of the body of revolution can be determined by integration through the revolution of an elemental area dA. Imply 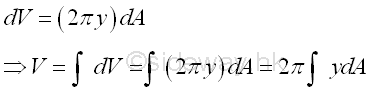
The volume V can be rearranged in the form of the integral of the first moment of an elemental area, which can also be expressed in terms of the centrod of the generating area, Imply 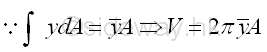
Applications of Theorems of Pappus-GuldinusThe Theorems of Pappus-Guldinus provides a simple relationship between the area of surface of revolution or the volume of body of revolution and the centroid of the generating plane curve or the centroid of the generating plane area. Therefore the Theorems of Pappus-Guldinus can be used to determine the area of surface of revolution and the volume of body of revolution from the generating curve and the generating area accordingly. And the centroid of a generating plane curve and the centroid of a generating plane area can also be determined from the surface of revolution and body of revolution accordingly. Surface of RevolutionCylinder 
Area of cylinder of surface of revolution is 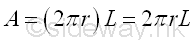
Area of cylinder of surface of revolution by theorem of Pappus-Guldinus is 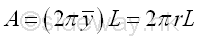
Cone 
Area of cone of surface of revolution is 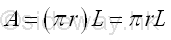
Area of cone of surface of revolution by theorem of Pappus-Guldinus is 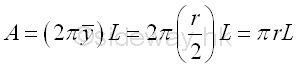
Sphere 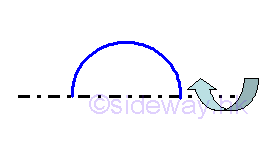
Area of sphere of surface of revolution is 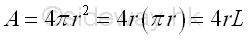
Area of sphere of surface of revolution by theorem of Pappus-Guldinus is 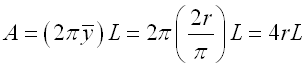
Torus 
Area of torus of surface of revolution is 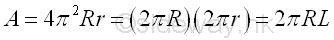
Area of torus of surface of revolution by theorem of Pappus-Guldinus is 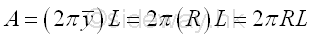
Solid of RevolutionCylinder 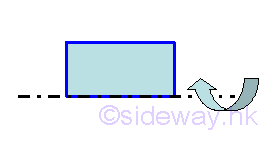
Volume of cylinder of body of revolution is 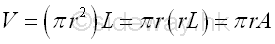
Volume of cylinder of body of revolution by theorem of Pappus-Guldinus is 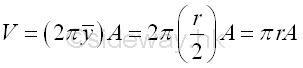
Cone 
Volume of cone of surface of revolution is 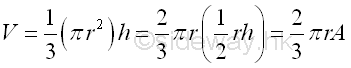
Volume of cone of surface of revolution by theorem of Pappus-Guldinus is 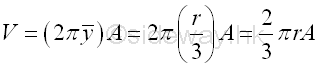
Sphere 
Volume of sphere of surface of revolution is 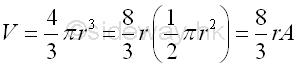
Volume of sphere of surface of revolution by theorem of Pappus-Guldinus is 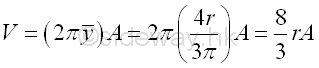
Torus 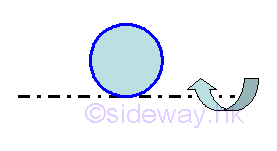
Volume of torus of surface of revolution is 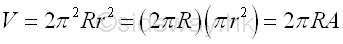
Volume of torus of surface of revolution by theorem of Pappus-Guldinus is 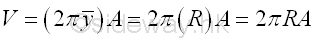
|
Sideway BICK Blog 09/07 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

