 Sideway
BICK BLOG from Sideway
Sideway
BICK BLOG from Sideway
|
Link:http://output.to/sideway/default.asp?qno=120700001 Centroid of 3D Body Centroid of 3D BodyThe centroid of 3D Body is determined by the first moment of a three dimensional body with the method of the first moment of volume. 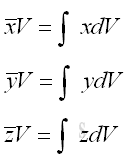
Centroids of VolumesThe using of unit elemental volume of an object to determine the centroid of a 3D body volume can be expressed as 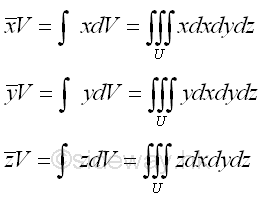
Centroid by IntegrationA triple integation is needed to evaluate with respect to the three varables. Similar to finding the volume of a 3D object body, the centroid of a 3D volume can usually be determined by performing a single integration or a double integration also. Centroid by Double IntegrationThe unit elemental volumes of an object used to determine the centroid of a 3D body can be rearranged into grouped elemental volumes. Imply 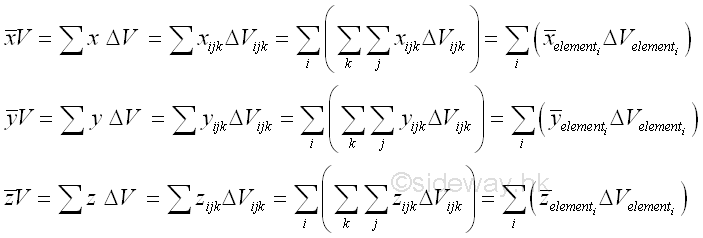
After the grouping of unit elemental volumes into one elemental volume, the coordinates of the centroid of a volume can also be determined by double integration in a similar way by considering the centroid of each elemental volume block. Imply 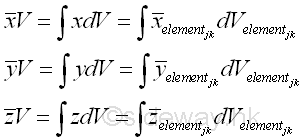
Centroid of Volume by Double Integration
For example, the signed volume of the 3D ellipic cylinder is bounded by surfaces in rectangular form , Imply 
The unit element volume of a region can be grouped into either a small vertical rectangular block or a small horizontal rectangular block . And the elemental volume ΔV becomes 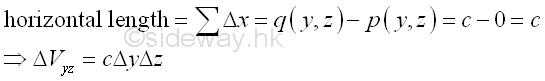
Considering the small horizontal rectangular block as the element volume, the centroid of the rectangular block can be determined by a single integration through sweeping the elemental centroid of the elemental rectangular block along the rectangular coordinate axis accordingly. Imply By sweeping the element of horizontal rectangular block along x axis horizontally Centroid of horizontal rectangular block. Imply 
Therefore, centroid of the bounded volume is 
Centroid by Single IntegrationThe unit elemental volumes of an object used to determine the centroid of a 3D body can be rearranged into grouped elemental volumes. Imply 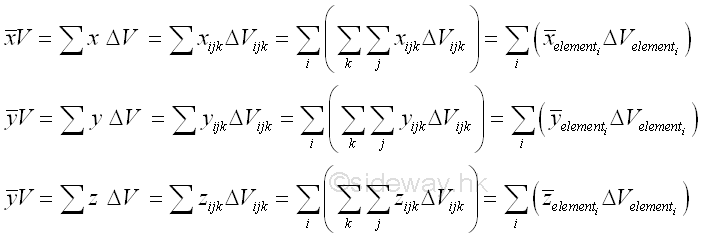
After the grouping of unit elemental volumes into one elemental volume, the coordinates of the centroid of a volume can also be determined by one single integration in a similar way by considering the centroid of each elemental volume block. Imply 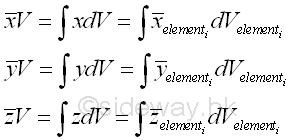
Centroid of Volume by Double IntegrationVolume by Single Integration
For example, the signed volume of the 3D ellipic cylinder is bounded by surfaces in rectangular form , Imply 
The unit element volume of a region can be grouped into either a thin vertical plane sheet or a thin horizontal plane sheet . And the elemental volume ΔV becomes 
Considering the thin vertical plane sheet as the element volume, the centroid of the thin vertical plane sheet can be determined by a double integration through sweeping the elemental centroid of the elemental plane sheet along the rectangular coordinate axis accordingly. Imply By staring with sweeping the element of vertical plane sheet along y axis horizontally Centroid of vertical plane sheet. Imply 
Therefore, centroid of the bounded volume is 
|
Sideway BICK Blog 03/07 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

