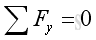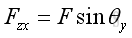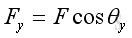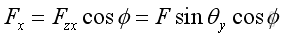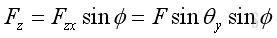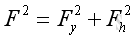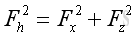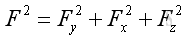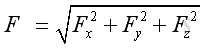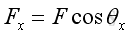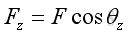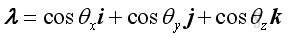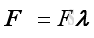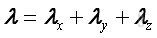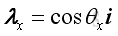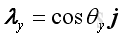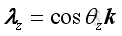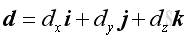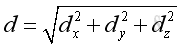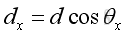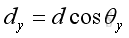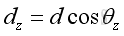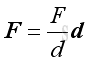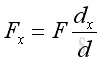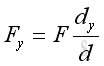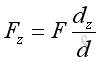Sideway
BICK BLOG from Sideway
Sideway
BICK BLOG from Sideway
|
Link:http://output.to/sideway/default.asp?qno=110400006 Forces in a Plane ForcesThe effect of force on an object can be characterized by its point of application, magnitude, and direction. As force has both magnitude and direction, it is a vector quantity. The unit of force is Newton. Force Vectors A force vector can be represented by an arrow with the length of arrow represents the magnitude of the force, the angle between the arrow and the coordinate axis defines the direction of force indicated by the line of action, and the arrow head indicates the sense of direction. 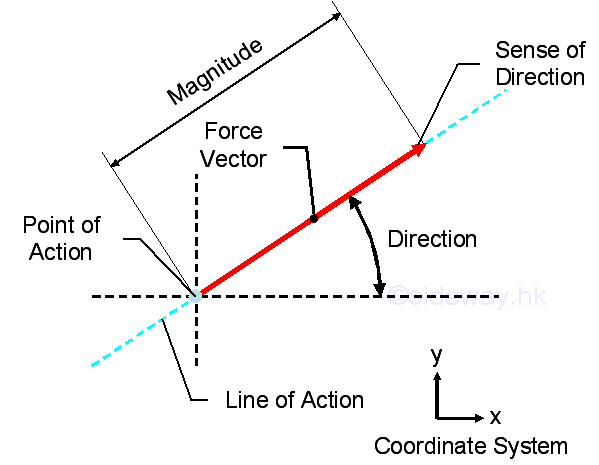
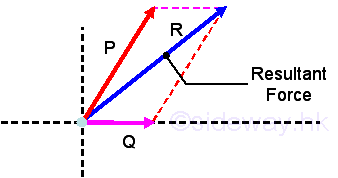
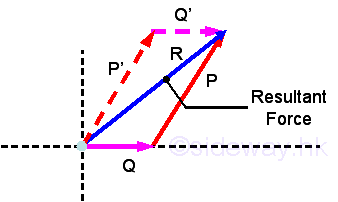
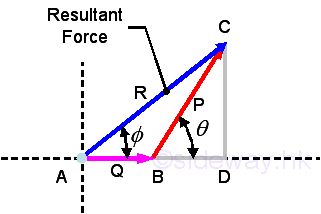
Forces in a Plane When more than one force act on a point, they can be replaced by a single resultant force with teh same effect on the point of action. 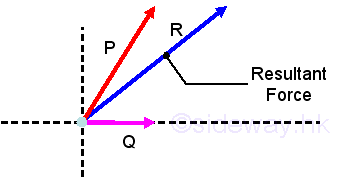
The resultant force can be determined by means of vector addition.
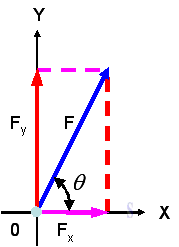
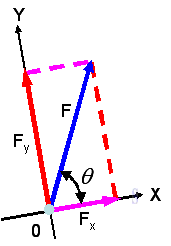
Force decomposition From the parallelogram Law, force can be resolved into two components. When the two components are perpendicular to each other in the form of a rectangle, they are called rectangular components.
Assumed two unit vectors, i and j, with unit magnitude along the x and y axis. Then
The two components of the force vector can be obtained by
The magnitude of the force vector can also be obtained by
And the direction of the force vector can also be obtained by 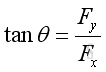
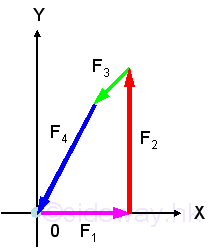
Force Equilibrium According to Newton's first law of motion, when a particle is in equilibrium, the resultant of all the forces acting on it is zero. That is 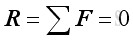
And graphically in the form of force polygon,
When there are only three applied forces, the problem can be reduced to a force triangle and be solved by trigonometry. Analytically, forces can be resolved into rectangular components to form the equations of equilibrium. Imply 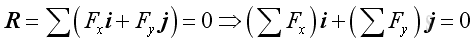
Therefore,
Link:http://output.to/sideway/default.asp?qno=110400005 Forces in Space Forces in SpaceIn practical applications, forces are usually involved in three dimensional space. Forces in a plane is only a special three dimensional case with the third direction equals to zero. Force Decomposition A force can be represented by a force vector, F, in three dimensional space. The force can be regarded as a plane force by assuming a plane passing through the force vector and normal to coordinate plane zx. And therefore force, F can be decomposed into a force, Fy along y axis and a force, Fzx in plane zx. Similarly, force, Fzx in plane zx can further be decomposed into a force, Fx along x axis and a force, Fz along z axis. 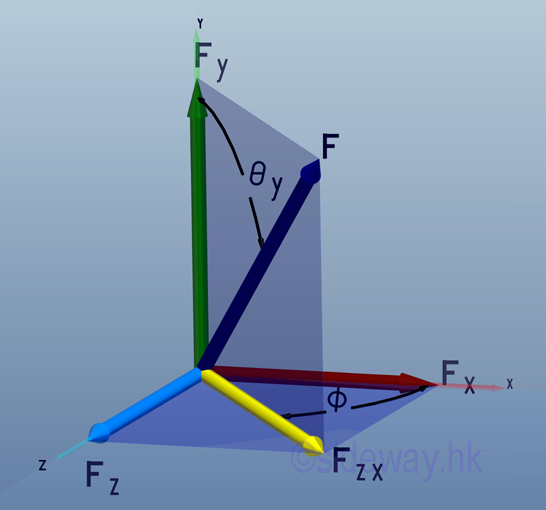
Therefore force vector, F, in three dimensional space can be decomposed into Fx, Fy, and Fz. Applying the laws of trigonometric, the magnitude of the three rectangular force vector components are:
And the magnitude of force vector, F, can be obtained by applying the Pythagorean theorem, imply:
The resultant force vector, F, can be obtained by vector addition of the three rectangular force vector components by applying Parallelogram Law, imply: 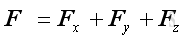
Assuming three unit vectors, i, j, and k, with unit magnitude along the x, y, and z axis. then 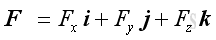
Imply 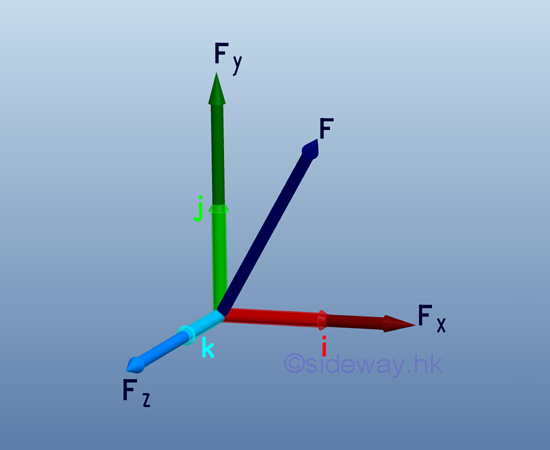
The three rectangular force vector components of the resultant force vector, F, can be arranged in a box, imply: 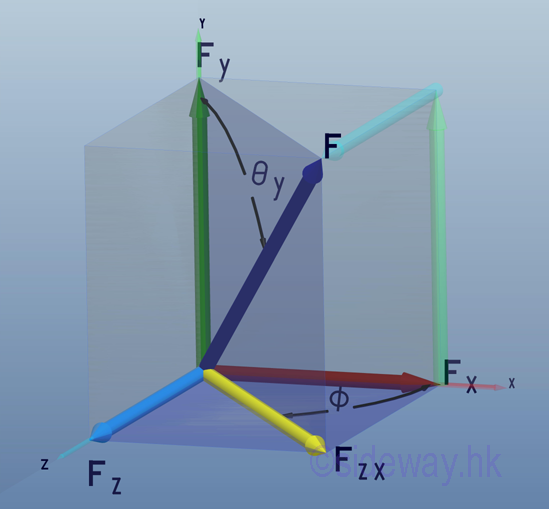
Direction Cosines The direction of the force vector, F can be defined by the angles formed by the force vector and the three coordinate axes, θx, θy, and θz. Imply 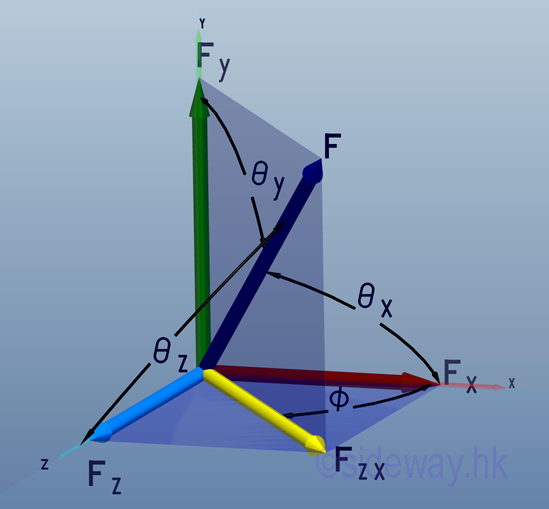
The magnitude of the three rectangular force vector components can be defined as:
The cosine of θx, θy, and θz are known as the direction cosines of the force vector, F. And the force vector becomes two dimensional force when one of the direction cosines equal to zero, that is angle equals 90 degree. The magnitude of force vector, F can therefore be expressed in terms of direction cosines as following: 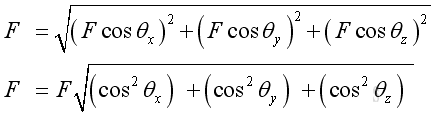
Imply the sum of the squares of direction consines equals to 1, that is: 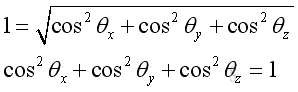
And the values of direction consines or the angles are not independent. The force vector, F can also be expressed in terms of unit coordinate vectors and direction cosines as following: 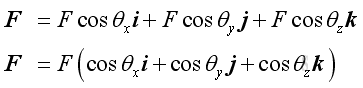
The format of the force vector expression can be treated as the product of the force magnitude and the unit direction vector. Let λ be the unit direction vector. Then
Similarly, the unit direction vector can also decomposed to three rectangular vectors:
The magnitude of the unit direction vector equals to one because: 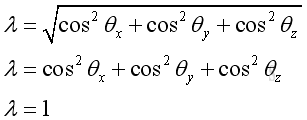
The relationship of force vectors and unit vectors is: 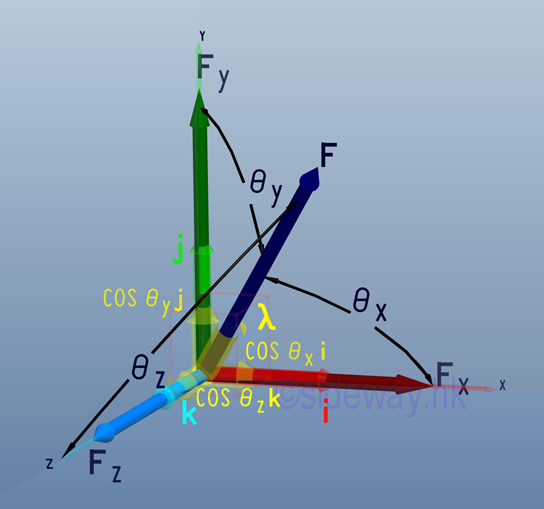
Laws of Trigonometric Relations The direction of a force in space along the line of action can also be respresented by a relative position vector, d. 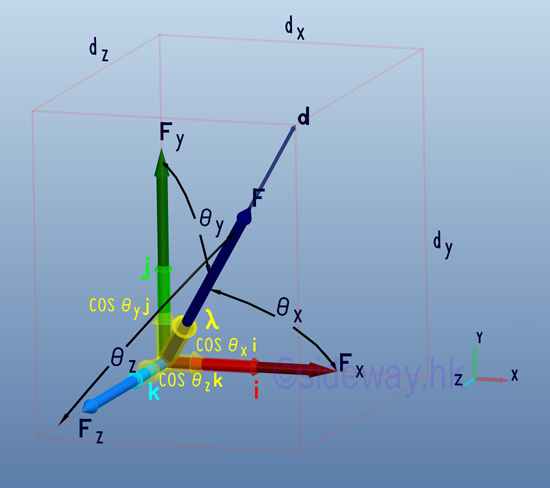
Similar to the force vector, F, the relative position vector, d can be expressed as:
Applying the laws of trigonometric relations, imply: 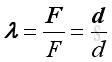
And:
|
Sideway BICK Blog 30/04 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
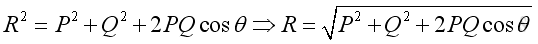
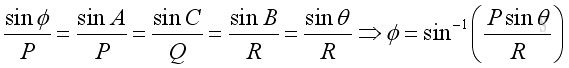
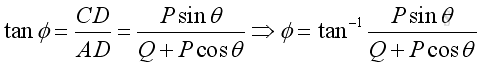
 or
or
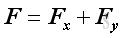 ,
,
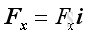 , and
, and
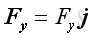 , imply
, imply
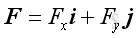
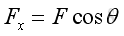 and
and
 , imply
, imply
 and
and