 Sideway
BICK BLOG from Sideway
Sideway
BICK BLOG from Sideway
|
Link:http://output.to/sideway/default.asp?qno=130100007 Calculus, Instantaneous Change, Differential Change Instantaneous ChangeInstantaneous change is the fundamental idea of calculus by making use of the concept of limit for a function to study the infinitesimal change of the function at an tiny instant on the interval of the continuous function. Infinitesimal ChangeA small increment or decrement usually refers to a small but finite change in the independent variable or the functional value of a function avaiable. When this small finite change becomes very small, then the very small finite change is called Delta. Imply 
When taking limit, the very small finite change becomes a tiny infinitely small change, the infinitesimal change. The infinitesimal change is called delta. Imply 
Instantaneous Change of a funtionFor a continuous function, when taking limit as x approaches c or Δx approaches 0, the limit of the function at x=c is equal to the functional value of the function at x=c. Since c can be any number, by considering the functional value y of the functaion at x as the instantaneous value f(x) of the function at x, the infinitesimal change δy of the function at x can then be considered as the instantaneous change of the functional value of a function at x due to the infinitesimal change δx of the independenc variable. Imply 
Differential Change of a funtionDifferential or Differential change is an infinitesimal change of a function or independent variable. A differential is an indivisible extreme small quantity of the functional value or the independent variable value of a function. A differential change is therefore denoted by a prefix character "d". Imply 
The function y=f(x) is a function of x only. The differential change dy is a function of x and dx. Since the differential change dy is derived from the function y, there is a close relation between the differential change dy and the function y. It is possible to develop the differential change dy in the form of g(x)dx by approximation. Imply 
When taking limit as δx approaches 0, the differential dy can be expressed as a functional relationship with the differential dx. The function g(x) is derived from the function f(x) and is also a function of x only. By expressing the differential change dy in the form of g(x)dx, a simple functional relationship between the differential change dx and the differential change dy can then be established. This expression is also the fundamental of "calculus of differentiation" and "calculus of integration". Ratio of Differential Changes of a functionCalculus of differentiation is the study of ratio of the differential changes of a function. Since the relation between the differential of the functional value and the differential of the independent variable value is related by a function, a differential change ratio between the differential changes dy and dx can be obtained by dividing both sides of the expression by the differential change dx. Imply 
The function g(x) becomes the differential change ratio. Since the function g(x) is derived from the function f(x), the differential change ratio g(x) is the rate of the differential change dy of the functional value y=f(x) over the differential change dx of the independent variable value x at x and is also a function of x only. By the concept of limit, the differential change ratio can be expressed in the form of instantaneous rate of change of a function y=f(x) when x approaching a. Imply 
By taking the limit as x approaches a, the instantaneous rate of change of a function at x=a is called the derivative f'(x) of a function f(x) at x=a. 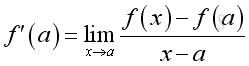
Summation of Differential changes of a functionCalculus of integration is the study of summation of the differentials of a function. Since the differential dy of the functional value y can be expressed in term of the differential dx of the independent variable value x, the difference between two functional values can be obtained by the summation of the differential changes dx over the interval of the independent variable value x. Imply 
The function g(x) derived from the function f(x) can be used to determine the difference between two functional values of the function y=f(x). By the concept of limit, when taking limit as n approaches infinity, the difference between two functional values of the function y=f(x) on internal [x1,xn] is equal to the sum of the differential changes dy on the internal [x1,xn]. If the differential dy is expressed in term of the rate of differential changes g(x), then the difference between two functional values of the function y=f(x) when x approaching a is 
By taking the limit as the differential dx or du approaches 0, the sum of individual signed area bounded by the function g(u) on the interval [x,a] is called the integral f(u) of a function g(x) on the interval u=[x,a]. 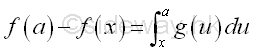
|
Sideway BICK Blog 29/01 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

