 Sideway
BICK BLOG from Sideway
Sideway
BICK BLOG from Sideway
|
Link:http://output.to/sideway/default.asp?qno=141100002 Mechanics Kinetics Energy Kinetics: Work and EnergyWork is a concept to describe the motion of an object by force and displacement mechanically. Energy is another concept to describe the kinetic motion of an object through a physical approach. Energy of the Motion of an ObjectBy Newton's Second Law, the resultant force acting on an object is equal to the time rate of change of the particle's linear momentum. For the kinetic motion of the object, an energy concept is used as the property of the object to described the kinetic motion of an object. Kinetic energy is a concept defined to quantify the kinetic motion of an object by mass and velocity physically. In other words, the physical kinetic motion of an object in terms of kinetic energy is used to describe the same mechanical kinetic motion of an object in terms of work. Therefore, Newton's second law can be used to convert equation of work into equation of kinetic energy. Kinetic Energy of the Motion of an Object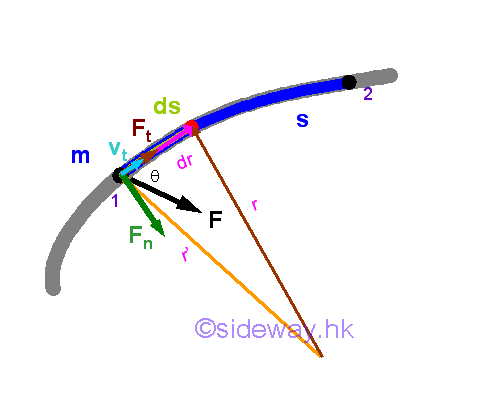
The mechanical action applied to displace an object due to an applied force can be transformed to the dynamic equation of the object by appling the Newton's second law of motion. And the equation of kinetic energy of the motion of an object due to the work done by the applied force can then be expressed in terms of dynamic quantities, momentum and velocity through terms rearrangement. 
Assume the initial velocity of an static object is equal to zero at an initial position, the kinetic energy of an object in motion with speed v at position 1 is equal to (mv2)/2. As work is a scalar quantity, the kinetic energy of an object is also a scalar quantity. Since Newton's second law is derived with respect to a newtonian frame of reference, the speed v of an object used to determine the kinetic energy should also be measured with respect to the same newtonian frame of reference as used in measuring the work done on the object. 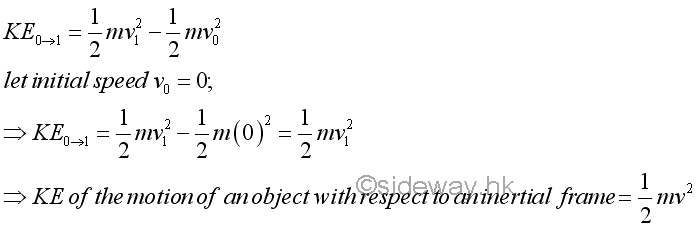
Although both work and kinetic energy are scalar quantity used to describe the motion of an object, there are a slightly difference between work and energy. With respect to an inertial frame of reference, work is only done if an object is displaced when a force acting upon the object. Therefore work is an quantity used to describe the displacement of an object and there is no work done with respect to the same position in an inertial frame of reference. With respect to an inertial frame of reference, kinetic energy is an quantity used to describe the kinetic motion of an object asscociated with the speed measurement of the object of mass m. The kinetic energy of an object is always greater than zero when the speed measurement of the object at a position with respect to an inertial frame of reference is not equal to zero. And therefore the kinetic energy of an object at different positions can be compared. Principle of Work and EnergyFor a kinetic motion of an object moving under a force from position 1 to position 2, work is done by the force to cause the displacement or change in position of an object. If the force is conservative and there is no other external force to cause the change in position, the work of the force must be equal to the change in kinetic energy of the object as shown in the derivation of the infinitesimal physical motion from the infinitesimal mechanical action. Therefore, the kinetic energy of an object at the destination position can be obtained by adding the additional work done on the object through the initial position to the destination position with respect to a newtonian frame of reference. 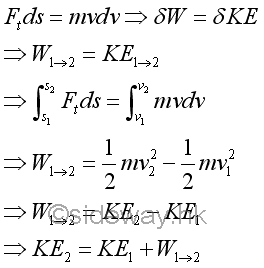
Kinetic energy of an object is a scalar quantity, which does not depend on the direction of the motion of the object and is always greater than or equal to zero. Although work is also a scalar quantity, work can be either positive or negative depending the direction of the force with respect to the direction of the motion. Since both work and kinetic energy are scalar quantities, the kinetic energy of an object due to the work can be computed as a simple algebraic sum without considering the directions of force and velocity. In a general sense, a positive work increases the kinetic energy of an object, while a negative work reduces the kinetic energy of an obect. In other words, the kinetic energy of an object can be interpreted as the capability of doing work that associated with the speed of the object. However, the kinetice energy of an object can not be smaller than zero with respect to the same newtonian frame of reference. 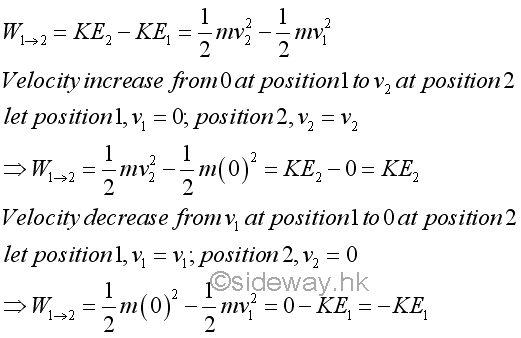
Since work is a scalar quantity depending on the direction of the force with respect to the direction of the motion only, the total work done on an object can also be computed as a simple algebraic sum of work done by individual force accordingly as used in component decomposition or coordinate system transformation. 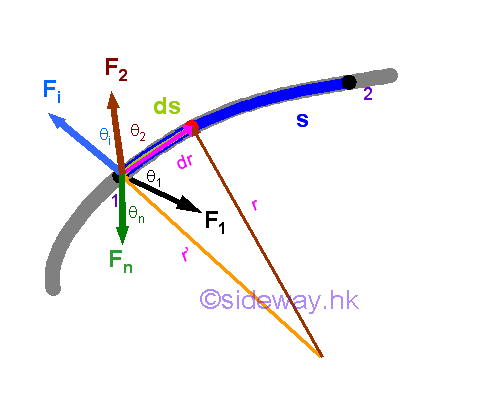
Imply 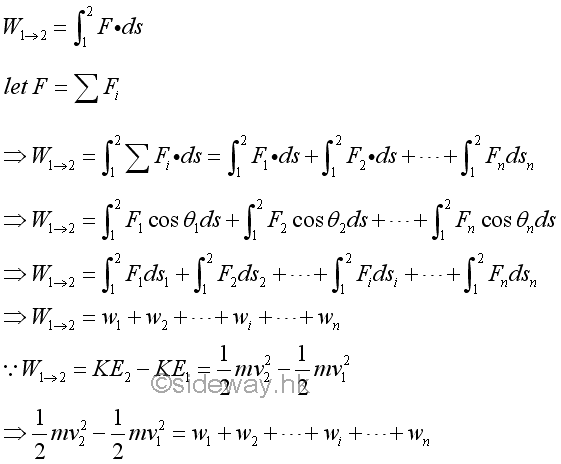
Work and Kinetic Energy of a Pendulum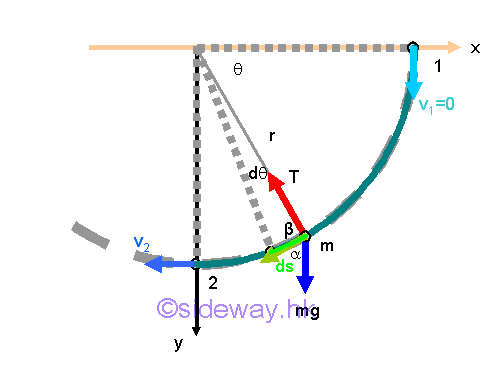
For example, a pendulum consists a bob of weight mg suspended by a weightless string of length r. When the pendulum is released at position 1 with initial velocity v1, and the bob swings through a lower position 2, at which the instantaneous velocity is equal to v2, work is done by forces acting on the bob, and the kinetic energy of the bob is changed accordingly also. Since the instantaneous velocity of the bob is always equal to the tangential velocity of the bob which is also equal to the speed of the bob. By definition, the kinetic energy of the bob at any position depends on the mass and speed only. Imply 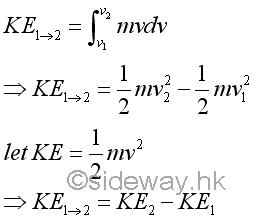
Similarly by definition, the work done on the bob by the force acting upon the bob from position 1 to position 2 can be obtained by the infinitesimal work done through the path travelled. Imply 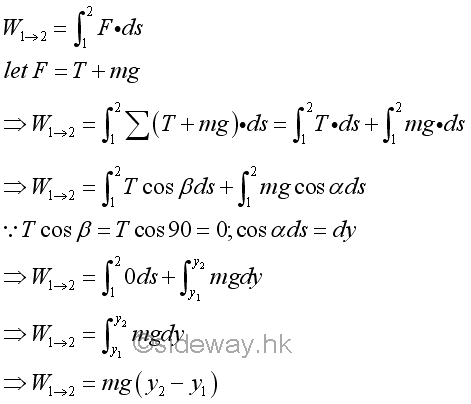
By the principle of work and energy, the change in kinetic energy of the bob between two positions is equal to the work done on the bob by all external forces acting upon the bob. That is 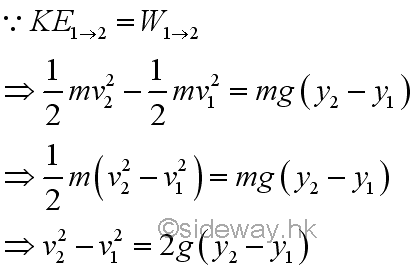
If the bob releases from a horizontal position 1 at y equals to 0 with initial velocity v1 equals to zero and swings through the vertial position 2 at y equals to r, the change in kinetic energy and the work done on the bob can be determined by applying the principle of work and energy. Imply 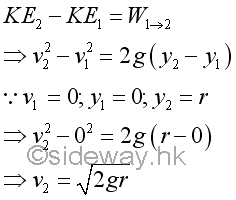
The princeiple of work and energy can be used to derive a simple relationship between velocity, acceleration and useful travelled distance. However when a force is normal to the path of the bob, the force does no work and will not be considered in the calculation using the principle of work and energy. Therefore Newton's second law or dynamic equilibrium equations are also needed to be used in solving the problem. 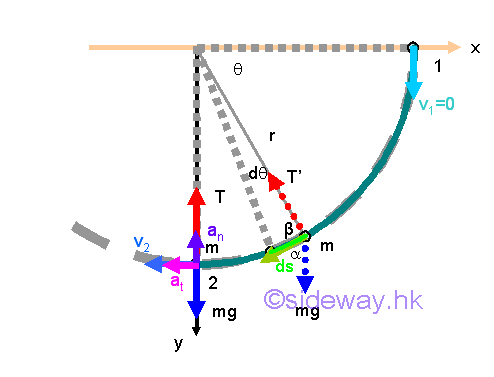
At position 2, the dynamic equilibrium equations can be expressed in terms of tangential and normal components. Since the motion of a pendulum undergoes a vertical circular motion, both the tension T in the string and the tangential velocity of the bob vary with the position of the bob. But at the vertical position 2, the tension T in the string and the tangential velocity of the bob are in maximum values. Therefore, the instantaneous tangential acceleration of the bob at position 2 is equal to zero. Imply 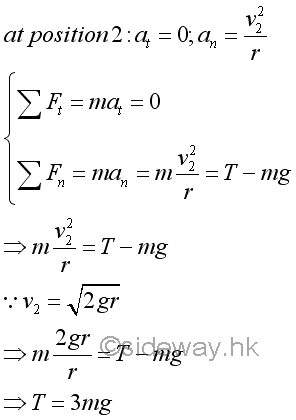
|
Sideway BICK Blog 25/11 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

