Internal Forces in Beams

The shearing forces and bending moments due to concentrated load and distributed load in a statically determinate beam can be determined by the equilibrium equations. Using the standard convention, the distribution of internal forces in a beam can be represented graphically by plotting the values of shear or bending moment against the distance from one end of the beam. Since both shear and bending moment in the beam is created by the applied load, relations among load, shear and bending can be used to develope formulas for calculating load, shear and bending moment in the beam. In general, relations among load, shear and bending moment can therefore be applied to the combination of concentrated and uniformly distributed loads and concentrated couple.

Simply Supported Beam with Concentrated and Unformly Distributed Load Example

For example, ignoring the horizontal forces, a simply supported beam with concentrated load P1 at the middle of the beam and uniformly distributed load of w per unit length over the span LAB of the beam.

For the uniformly distributed load of w per unit length over the span LAB of the beam, the uniformly distributed load can be represented by an equivalent concentrated force of P2=wLAB acting at the centroid of the distributed load, i.e. the middle point C of point A and point B, on the simply supported beam.  Together with a concentrated load P1 acting at the middle point C of the beam, the Reaction forces can also be determined by setting up the equilibrium equations. Imply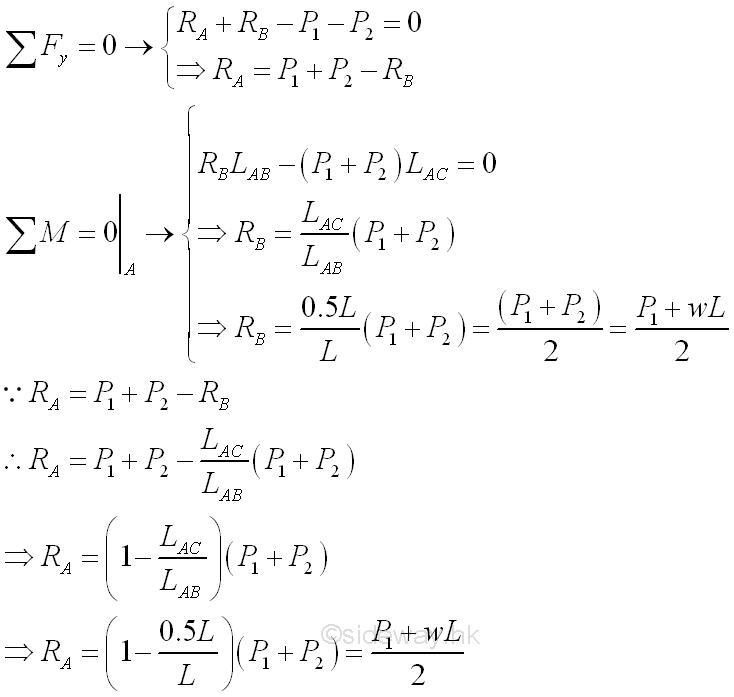

External Loads Diagram

The diagram of external load, shear and bending moment is not a vector diagram according to the rectangular coordinate but a signed diagram of the sense of the external load, shear and bending moment used in defining the standard convention of the internal forces. All external forces applied on the beam can be drawn on the external loads diagram according to the convention used. For example  the concentrated load P1 and the distributed load w is positive as the load is pointing downward and the reaction force is negative as the reaction is pointing upward.  Imply the load curve

And the accumulative load diagram is

Shear Diagram

In general, the internal force, shear, can be considered as the reaction forces of the accumulated external forces acting on the imaginary beam section considered. And this is the concept of the negative signed area, i.e. Vn=-∑Fi=∑ΔVi=-∑wiΔx under load curve. The concept can be applied to both concentrated and distributed loads. A concentrated load causes a discontinuous jump of shear while a distributed load causes a continuous change of internal force, shear.

Start drawing the shear diagram from point A at the left side of the beam at which the beam is in equilibrium and the shear is assumed to be equal to zero. Imply

The three concentrated external forces cause three step jumps on the shear diagram. The shear curve is a piecewise curve of slope -w throughout with a jump at position C. at which the concentrated force applied. For a distributed load, the shear curve is a oblique straight line drawn from the shear of last imaginary element. The shear diagram is

The internal force, shear, acting on the imaginary element in the shear diagram is positive if the shear is the same sense as the standard convention used. Therefore the signed shear effefct due to the corresponding external force in the shear diagram is of the same sense as the external forces.

The shear diagram can be considered as the sum of shear due to the concentrated load and distributed load separately. Imply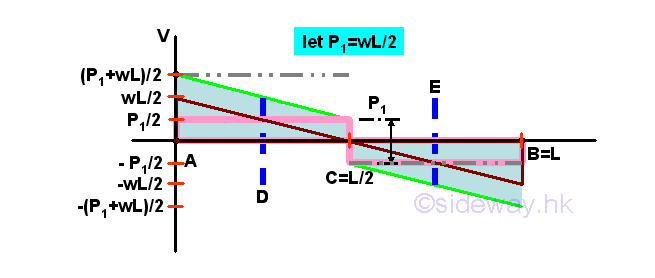

Bending Moment Diagram

Similarly, the internal force, bending moment, can also be considered as the reactive moment to balance the accumulated bending moment due to all external forces taking about the right hand side of the imaginary beam section considered. And this is the concept of the signed area, i.e. Mn=∑Vixi=∑ΔMi=∑∑ViΔx under shear curve. The concept can be applied to both concentrated and distributed loads. A concentrated load causes a single concentrated moment about the right hand side of a imaginary beam section while a distributed load causes a continuous concentrated moment about the right hand side of a imaginary beam section.

Start drawing the bending moment diagram from point A at the left side of the beam at which the beam is in equilibrium and the bending moment is assumed to be equal to zero. Imply

The bending moment curve is a piecewise parabolic curve of the second degree with maximum bending moment of P1L/4+wL^2/8 at position L/2, i.e. point C. Since the bending moment curve is a piecewise curve with a break at point C, the slope of the bending moment curve at the left hand side of point C is P1L/4+wL^2/8 and the slope of the bending moment curve at the right hand side of point C is -(P1L/4+wL^2/8). And both the bending moments at point A and point B are equal to zero. But the slope of bending moment curve at point A' is (P1+wL)/2 and the slope of the bending moment curve at point B' is -(P1+wL)/2. And from the results of dM/dx, there is no local maximum or mininimum on the two parabolic curve segment.

The bending moment diagram is

The bending moment diagram can be considered as the sum of bending moment due to the concentrated load and distributed load separately. Imply

Simply Supported Beam with Concentrated, Unformly Distributed Load and Concentrated Couple Example

For example, ignoring the horizontal forces, a simply supported beam with a concentrated load P and a concentrated couple M1 at the middle of the beam and uniformly distributed load of w per unit length over the span LAB of the beam.

For the uniformly distributed load of w per unit length over the span L of the beam, the uniformly distributed load can be represented by an equivalent concentrated force of P2=wL acting at the centroid of the distributed load, i.e. the middle point C of point A and point B, on the simply supported beam.  Together with a concentrated load P1 and a concentrated couple M1 acting at the middle point C of the beam, the reaction forces can also be determined by setting up the equilibrium equations. Imply

The additional concentrated couple M1 at the middle of the beam will create addional shear and bending moment in the beam. From standard shear and bending moment diagram, the shear diagram of a positive concentrated couple is

And the bending moment diagram of a positive concentrated couple is

Therefore the shear diagram by curve addition is

The shear diagram is

Similarly the bending moment diagram by curve addition is

The bending moment diagram is

Besides the sudden change in bending moment due to the addition of a concentrated couple on the beam. The additional concentrated couple will also create additional shear in the beam. Therefore both the additional shear and bending moment should be considered in both the shear difference and bending moment difference equations for plotting the shear diagram and the bending moment diagram.