 Sideway
BICK BLOG from Sideway
Sideway
BICK BLOG from Sideway
|
Link:http://output.to/sideway/default.asp?qno=100200007 Matrices MatricesMatricesA matrix, designated by a bold capital letter, is a collection of elements enclosed in brackets in the form of rectangular array with horizontal rows and vertical columns. A matrix is usually denoted by a upper case letter and an element of matrix is often denoted by a lower case letter with double subscript notation 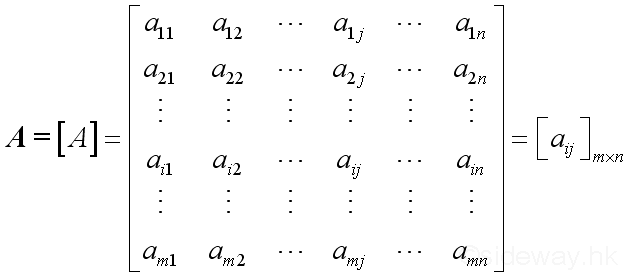
The matrix A is of order m x n with m rows and n columns. Row i of the matrix:
Column j of the matrix:
Element
Square MatrixA matrix with the same number of rows as columns, m = n is called a square matrix of order n. Principal Diagonal
The elements
TraceThe trace of a square matrix is the sum of the elements on the principal diagonal. 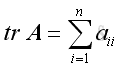
VectorFor a single row matrix, of order 1 x n, it is called a row vector or row matrix. For a single column matrix, of order m x 1, it is called a column vector or column matrix. A vector is usually represented by a lower case letter, e.g. a Zero MatrixIf a matrix of any order consists all elements zero, it is called a zero matrix or null matrix, O. Equality of Matrices,
|
Sideway BICK Blog 24/02 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
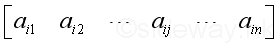 ;
;
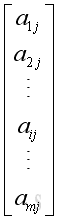
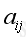 is the matrix content at the intersection of row
is the matrix content at the intersection of row 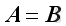
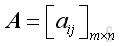 and
and
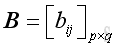 ,
,
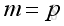 &
&
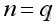 and the corresponding elements are equal,
and the corresponding elements are equal,
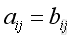 , then two matrices are equal,
, then two matrices are equal,

