 Sideway
BICK BLOG from Sideway
Sideway
BICK BLOG from Sideway
|
Link:http://output.to/sideway/default.asp?qno=110500013 Moment Moment of a ForceIn many practical applications, an object subjects to a system of forces cannot be treated as a single particle. By assuming the object as a collection of particles, forces can be considered as acting on different partilcles with different points of application on the object. The force acts on the particle at the point of application on the object will cause the particle to move or translate in the direction of the force. The force acts upon the whole object may therefore twist, or rotate the object. The tendency of a force to rotate an object about a point or an axis is called moment, or moment of a force. Rigid BodyTo simplify the problem, the interested object in elementary mechanics can be assumed to be a rigid body in which deformation is neglected when external forces exterted on it. The external forces are those external action acting on the object externally and causing it to move or to remain at rest. There are also internal forces which act between particles to hold particles together forming the rigid body or act between components to hold component parts together forming the rigid body, or the rigid structure. MomentThe moment of a force about a point is defined as the product of the force, F, along a line of action and the perpendicular distance, d, between the line of action of the force and the point of reference. Moment of a force about a point determines the tendency to rotate the object about the reference point. The reference point is the center of moment and the perpendicular distance is the moment arm or lever arm of the rotation. 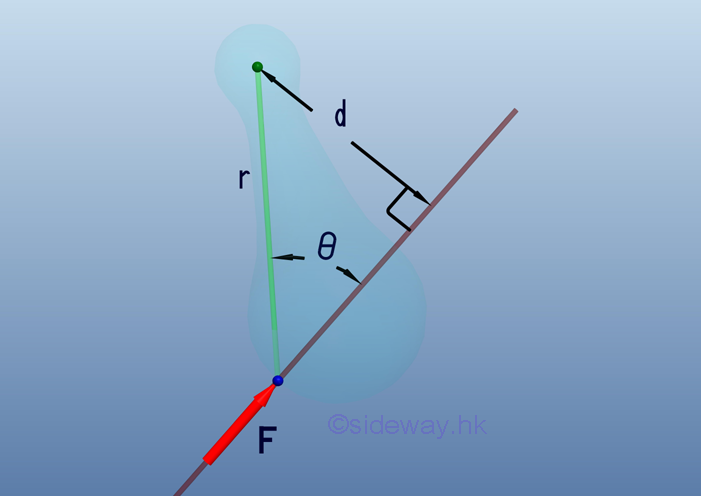
Therefore, the magnitude of the moment , M, concerning with the rotational force can be expressed as:
Moment also have both sense and direction. The sense of moment indicates the direction of the rotational force following the right hand rule. And the direction of moment specifies the axis of rotation associated with the rotational force. Therefore, a moment vector at the reference point can be used to represent the moment due to the force about a reference point 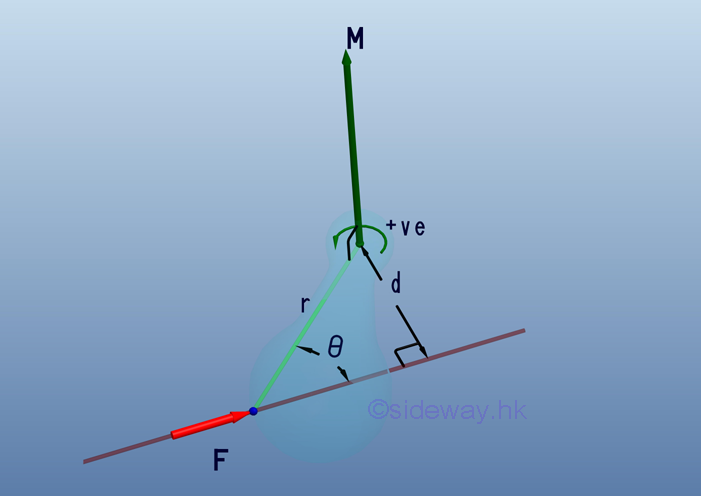
By the principle of transmissibility, the force, F, can be replaced by a force acting on a different point with the same magnitude and same direction along the same line of action without changing the conditions of equilibrium or motion of a rigid body. Link:http://output.to/sideway/default.asp?qno=110400007 Forces in Space Resultant Force The resultant force of concurrent forces in space can be represented by a force vector, R, in three dimensional space.
The most practical way of determining the resultant force in space is to add up their rectangular components respectively:
Imply:
Therefore: 
And similarly, the resultant force vector, R, can be expressed as:
Force Equilibrium According to Newton's first law of motion, when a particle is in equilibrium, the resultant of all the forces acting on it is zero. That is 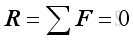
And graphically in the form of force polygon,
|
Sideway BICK Blog 21/05 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
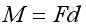 or
or
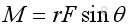

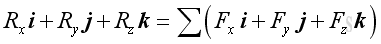
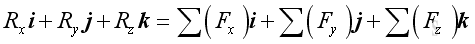
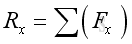
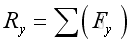
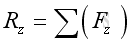





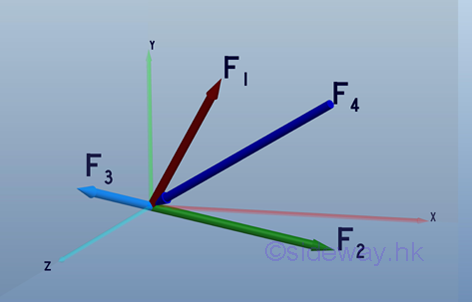 , imply
, imply


