 Sideway
BICK BLOG from Sideway
Sideway
BICK BLOG from Sideway
|
Link:http://output.to/sideway/default.asp?qno=141000001 Mechanics Kinetics Angular Momentum Particle Object Kinetics: Angular Momentum and MomentMomentum is a concept to measure the instantaneous inertia of an object in motion relative to a newtonian frame of reference. Moment is the concept of the tendency of an object rotating about a point or an axis. In kinetics, angular momentum or moment of momentum is defined as a concept to measure the instantaneous rotational motion of the inertia of an object in motion relative to a newtonian frame of reference about a point or an axis. Moment of resultant force is used to measure the rate of change of the angular momentum of an object about the same reference point or axis. And therefore the moment of an object is also an important characteristics of an object in motion. Angular Momentum of Particle ObjectMomentThe rate of change of the angular momentum of an object about a reference point can be determined by the resultant moment of the object about the reference using the concept of moment and Newton's second law of motion. 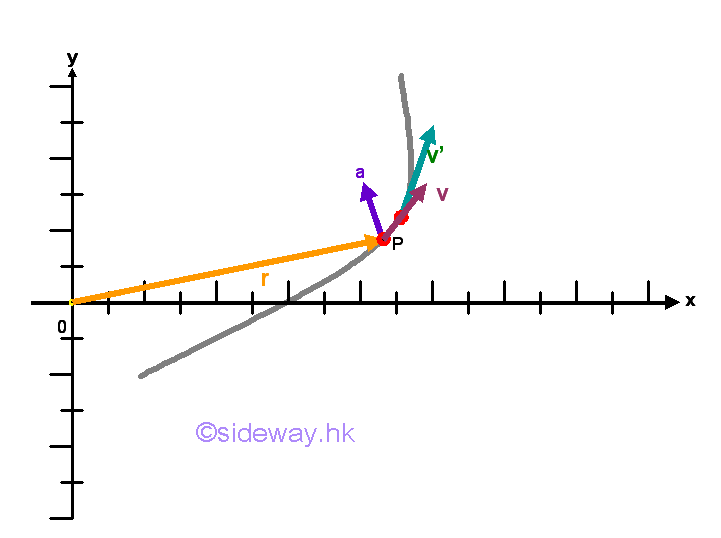
From Newton's second law of motion, an object will be accelerated if the the resultant force acting upon it is not equal to zero. Since mass is assumed to be a constant, the rate of change of the momentum of an object is equal to mass time acceleration which is equal to force by definition. In other word, the instantaneuous change in momentum is due to the resultant force. The acceleration of the object is proportional to the magnitude of the resultant force and the acceleration is in the direction of the resultant force. Since a force is needed to change the direction or magnitude of the motion of an object, the acceleration of an object is usually not collinear with the velocity of the object when the object is in curvilinear motion. Besides, moment or angular momentum is related to the rotational motion of an object, sometime it is more convenient to consider the polar coordinate system instead of rectangular coordinate system. 
Kinetic of MotionCarousel
The object on a carousel is undergoing a horizontal circular motion
with the
radius of the location of the object from the center is equal to constant r and
the carousel is rotated at constant speed. 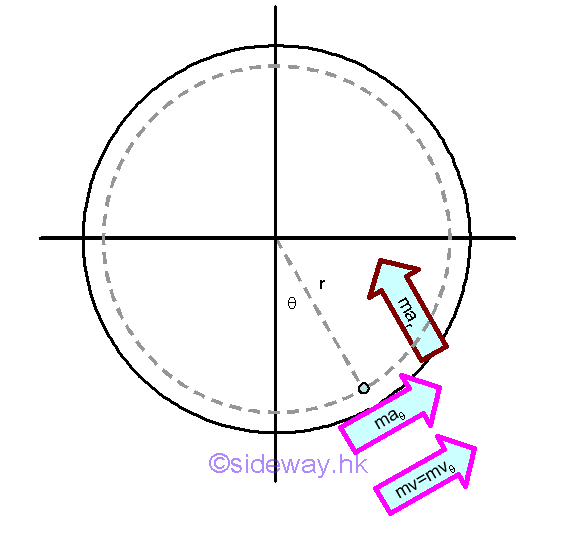
From Newton's second law of motion, an object will be accelerated if the the resultant force acting on it is not equal to zero. The acceleration of an object can be the change of the speed in magnitude as well as the change of the direction of the motion. From kinematics of the uniform horizontal circular motion with respect to the polar coordinate system, the radial acceleration component of an object due to the radial component of the resultant force, whch is used to change the direction of motion, is proportional to the square of the transverse velocity and inversely proportional to the radius of the circular motion. While the transverse acceleration component is equal to zero since the speed of the transverse velocity is a constant. 
Since the velocity of the object is not equal to zero, the momentum of the object with respect to the polar coordinate system is always not equal to zero. Although the magnitude of the velocity of the object is a constant, the direction of the velocity vector of the object is not a constant. Therefore the derivative of the momentum is not equal to zero and is equal to the radial component of the force vector only while the transverse component of the force vector is always equal to zero as the circular motion is a uniform motion. The negative sense of the resultant force vector means that the force is always towards the center of the cirular motion, or the origin of the polar coordinate system. The force acting on the object, which is observed with respect to the polar coordinate system of an inertial frame of reference, is called centripetal force as the force always points to the centre of the circular motion. But in daily life applications, people riding on a carousel always experiences a centrifugal force instead of a centripetal force. When studying the circular motion of an object with respect to the centre of the circular motion, an inertial reference frame, the inertia of the object is undergoing a centripetal force such that the motion of the object follows the circular path, or curvilinear path. But when studying the motion of the object with respect to the position of the object, a non-inertial reference frame, the inertial of the object is undergoing a centrifugal force to react against the acceleration of the centripetal force such that the motion of the object, in the view of the riding people, remains moving at a constant velocity of the same magnitude and direction. In general, with respect to an inertial reference frame, a centripetal force is needed to keep the people riding on the carousel to move in a circular path physically, while a centrifugal force is the reaction force used to retain the people riding on the carousel to move in constant velocity, that is moving along a straigh line virtually. For a uniform circular motion, the momentum vector of the object is always perpendicular to the position vector and the magnitudes of both the momentum vector and position vector are also a constant. The angular momentum of the object is therefore always equal to a constant. And the derivative of the angular momentum of the object or the resultant moment is always equal to zero. Fast Moving Projectiles Under a Central ForceA projectile is usually defined as an object with non-zero initial velocity moves along a path due mainly to gravity which pulls the projectile toward the center of the Earth. All objects projected near the Earth surface experiences a gravitational force. The only gravitational force acting upon the projectile will cause the object to free fall onto the surface of the Earth if the velocity of the projectile is not fast enough to overcome the force of attraction. But for a fast moving projectile, e.g. a satellite, the projectile can fall around the Earth if the velocity of the projectile is fast enough to balance the gravity. Newton's Law of Universal gravitation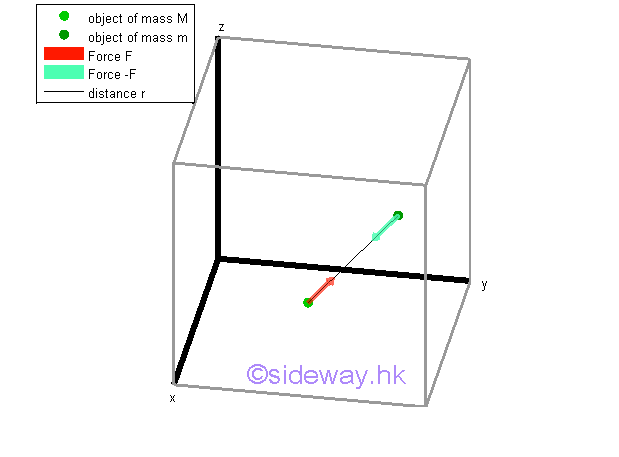
From Newton's law of universal gravitation, two particles of masses m and M, which locate at a distrance r apart from each other, will attract each other with equal and opposite forces F and -F with the line of action of forces along the line joining the two particles. The magnitude of the attraction force F is equal to 
For a rough estimation of the motion of the Moon from Newton, assuming the moon is a free projectile which is mainly attracted by the Earth toward the center of the Earth and is undergoing a circular motion. For a circular motion, the velocity of the object can be expressed in term of the circumference of the orbit 2πr over the period T and the centripetal force F is equal to mv2/r. Therefore, the centripetal force F can be expressed in term of the reciprocal of the square of period T. According to the Kepler's third law, the square of the orbital period of a planet motion is proportional to the cube of the semi-major axis of its orbit. And Newton's law of the inverse square can then be obtained by substitute r3 for T2. 
Since force is also proportional to acceleration, the acceleration is proprotional to the inverse square of radius also. 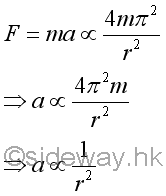
The acceleration of moon can therefore be approximated by the acceleration of object on the surface of the Earth. By equating equations of centripetal forces and assuming the distance of the Moon from the center of earth is equal to 60 earth radii, the period of the motion of moon can be estimated. 
The calculated orbital period is quite close to the measured orbital period of the Moon around the Earth is about 27.32days. This is a good approximation because the orbit of the Moon is elliptical with an eccentricity of about 0.055. 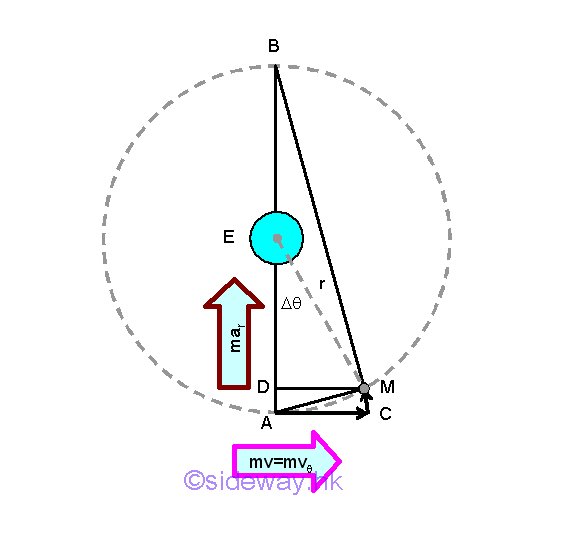
Similar to the projectile calculation on the surface of Earth, Newton applies the infinitesimal approach to calculate the falling of the Moon toward the Earth into a circular orbit as assumed. For example, assume arc AM be the falling path of the Moon in one minute, the falling path is not very large because the orbital period of the Moon around the Earth is about 27.24 days, the angle Δθ is only about 2π(1minute/27.24days)=0.00016 radian. The motion of the Moon can be resolved into two components, the natural linear motion AC and the free falling motion CM. When the travelled distance of the Moon is not very large, the free falling distance CM can be approximated by the length of line AD. Besides, line AM can also be assumed to equal to the arc AM of the Moon motion. There are two ways to calculate the vertial free falling distance AD, namely kinematically and geometrically. Kinematically, distance AD is equal 1/2at2=4.91. Geometrically, line AD can be determined by constructing two similar right angle triangles, AMB and ADM, with common angle MAD or BAM. Therefore AD/AM=AM/AB, imply AD=AM2/AB=(60re(0.00016))2/2(60re)=30re.=4.89. The falling motion of the Moon is quite close to calculated kinematic result. 
The two different approachs of finding the orbital period and the free falling distance of the Moon demonstrate that the falling of the Moon in the sky is also due to the gravity which causes the falling of an object on the surface of the Earth. Therefore the gravitational force is proportional to the mass of the moving object and inversely proportional to the square of the distance apart. As gravitational force is an attractive force between two object particles, Newton is therefore proposed that a universal force of gravitation F, which is proportional to the mass m and M, and inversely proportional to the square or their distance of separation r, always exists between two masses m and M from each other. That is 
The force exerted by the Earth on the object located on the surface of the Earth is called the weight of the object, which is defined as W=mg. 
Conservation of Angular Momentum Under a Central ForceThe assumed only attracting force acting on the Moon due to the Earth is called central force and the Earth is called the center of force. The motion of an object under a central force is not necessary to be undergoing a circular motion because the path of the moving object depends on both the velocity vector and the distance away from the attracting object. However, when the only force acting upon an object is always directed toward or away from a fixed point, the resultant moment about the fixed point is always equal to zero since the line of action of the resultant force, or the only attracting force, is alway passing through the fixed point. As resultant moment is equal to the rate of change of angular momentum, in other words, the anglur momentum of an object moving under a central force must be equal to a constant, that is in both magnitude and direction. 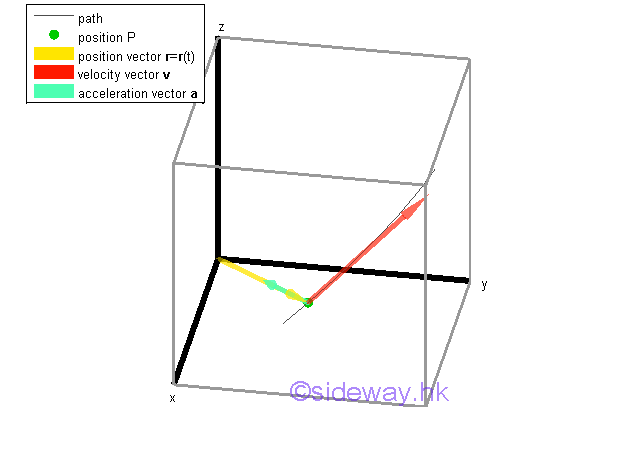
Since the angular momentum of an object moving under a central force is constant and there is only one central force acting on the object, the object must move in a fixed plane perpendicular to the angular momentum vector which can be defined by the initial position vector r and the initial velocity v of the object. In other words, both the position vector and velocity vector must be on the same plane. 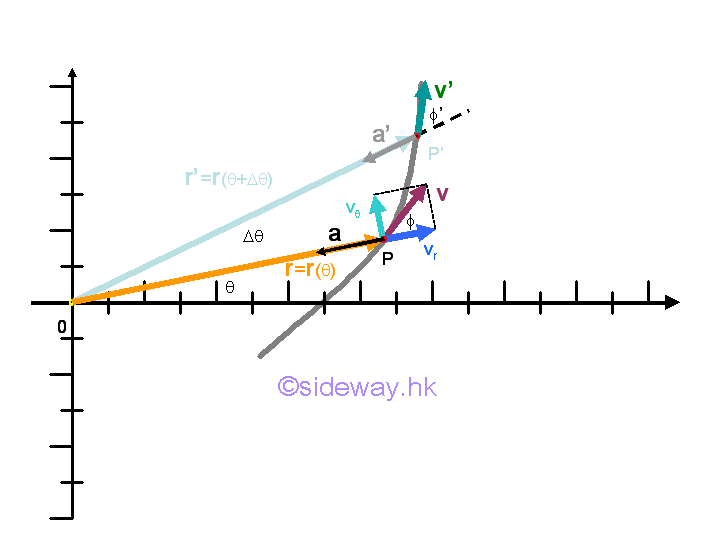
By expressing the definition of resultant moment in terms of the rate of change of the angular momentum, the angular momentum of an object moving under a central force is. 
The angular momentum vector obtained by the vector product is equal to 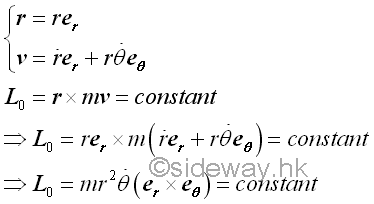
The magnitude of the angular momentum by definition is equal to the product of the radial magnitude of the position vector and the transverse magnitude of the momentum vector. 
Since the angular momentum of an object moving under a central force is always constant, the angular momentum of the object is conserved along the path of the motion. Therefore for a fixed mass, the product of the radial distance and the transverse velocity is alway equal to constant and is equal to the magnitude of the angular momentum vector per unit mass. 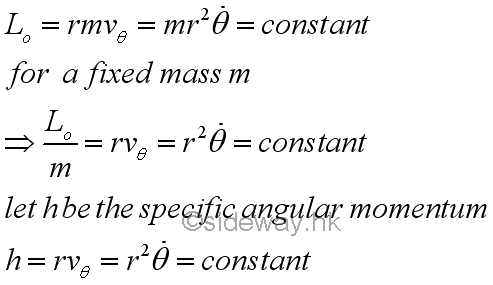
Geometrically, the angular momentum vector per unit mass can be expressed in terms of an infinitesimal area, that is dA=r(rdθ)/2, with respect to the time. And dA/dt is also called the areal velocity of an object. Therefore the magnitude of the angular moment per unit mass is equal to twice the areal velocity of the object. And the areal velocity of an object moves under a central force is also constant. 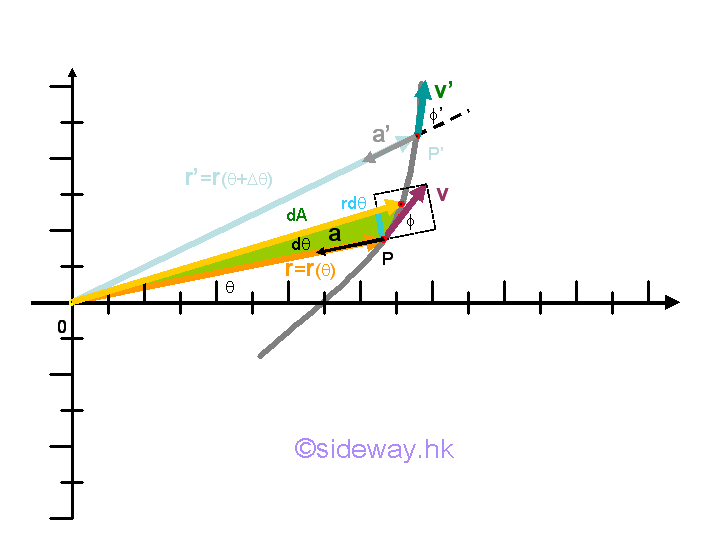
Trajectory of an Object Under a Central ForceSince an object moving under a central force is in equilibrium, the following dynamic equations can be obtained. 
From resultant radial forc e and resultant specific angular momentum, the second derivative of radius with respect to time can be determined. 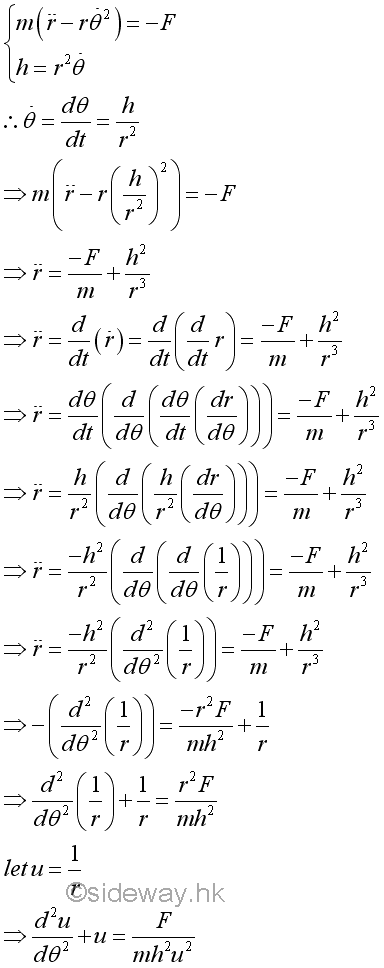
The central attraction force F between two objects can be determined by Newton's Law of Universal gravitation. And the equation is then equivalent to an inhomogeneous harmonic oscillator equation. 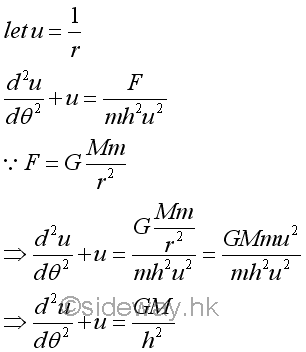
The central attraction force F between two objects can be determined by Newton's Law of Universal gravitation. And the equation is then equivalent to an inhomogeneous harmonic oscillator equation. The solution consists of two parts, a sinusoidally varying term of the homogeneous solution and an angle-independent term of the particular solution. The general form of the solution of the inhomogeneous harmonic oscillator equation can be expressed as 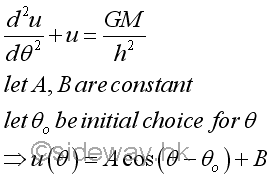
Therefore 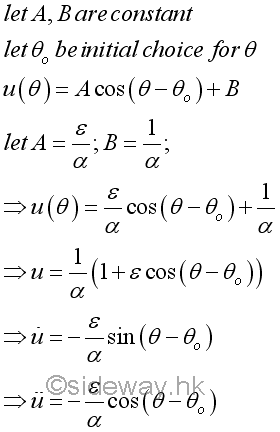
Imply 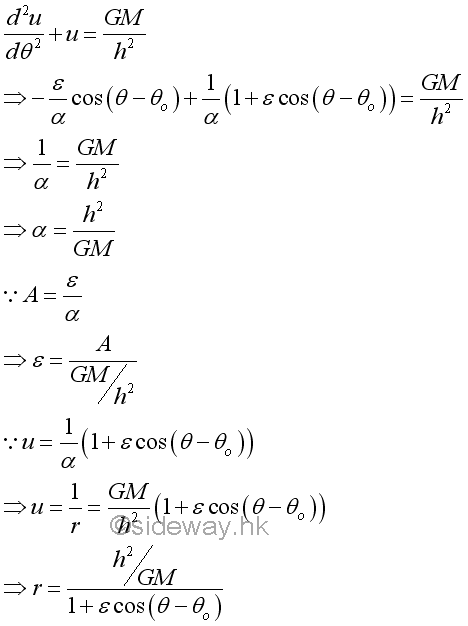
The equation is the polar equation of a conic section, that is ellipse, parabola, or hyperbola. Since the gravitational attraction force is generated by the Earth, the centre of the Earth is the origin of the polar coordinates r and θ, which is a focus of the conic section. By setting θo=0, the polar axis is one of the axes of symmetry. By assuming the general solution with +cos θ, the conic section has a vertical directrix to the right of the focus. 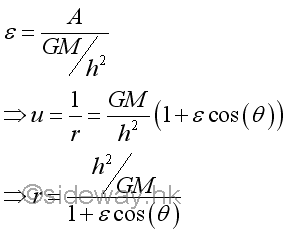
The eccentricity ε is equal to the ratio of A and GM/h2. Depending on the value of A, the equation represents three possible trajectories. Since cosine is an even function, cos(θ)=cos(-θ), all trajectories will be symmetric about the polar axis.
That is 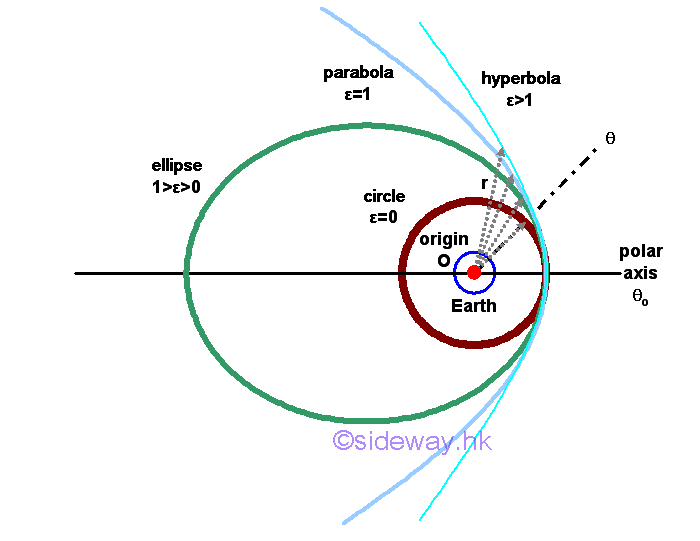
Escape Velocity of an Object Under a Central Force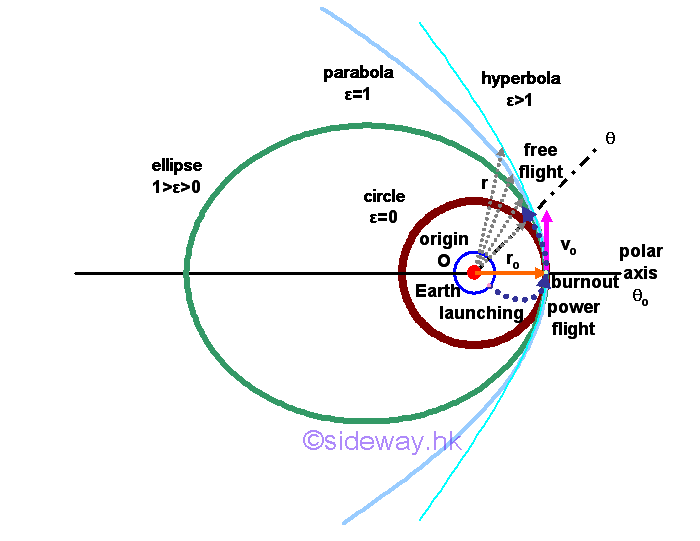
Unlike free projectile, when an object is launched from the Earth surface, the object is first undergoing a programmed power flight such that the velocity of the object is only parallel to the surface of the Earth at the last burning out stage of the object lunching. The object is then assumed to be a free flight with transverse component only under a central force after the object burns out. The radial radius and transverse velocity at the end of programmed power flight is equal to the initial radial radius ro and initial transverse velocity vo at the beginning of the free flight. Since the angular momentum per unit mass or specific angular momentum is constant, the angular momentum per unit mass can be expressed in terms of the initial radial radius ro and initial transverse velocity vo. And therefore the constant A of the trajectory equation can also be determined by the initial condition. 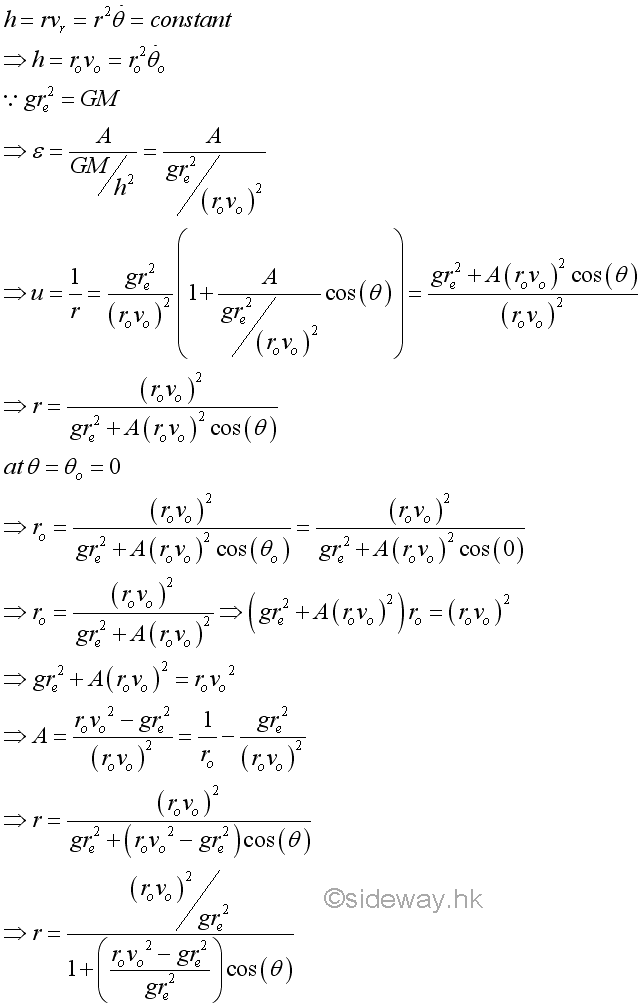
Therefore, the polar equation of the trajectory can also be expressed as in terms of the initial radial radius ro and initial transverse velocity vo. Since the type of conic sectional trajectory of the conic polar equation depends on the eccentricity ε of the equation, the type of conic section depends on initial transverse velocity vo for each initial radial radius ro . 
When the eccentricity ε or constant A equals to zero, the trajectory of the object is a circular orbit, on which the object rotates around the focus or the center at a fixed radial radius. 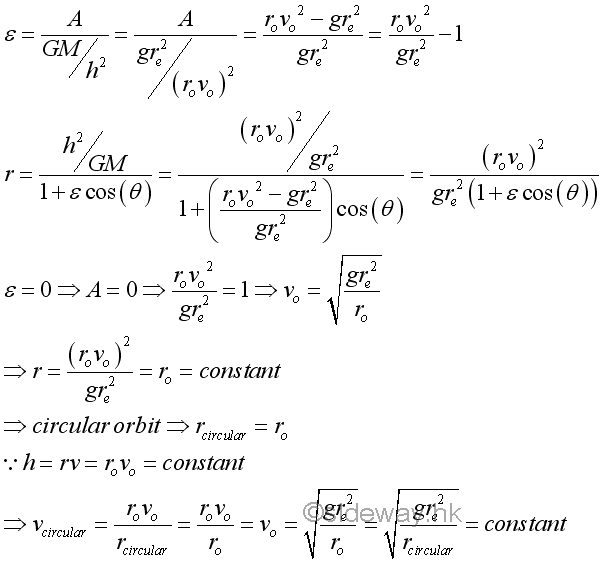
When the eccentricity ε is of the range 0<ε<1 or constant A is of the range 0<A<g(re)2/(rovo)2, the trajectory of the object is an elliptic orbit, on which the object rotates around the focus on the right hand side with finite radial radius. The point of the orbit closest to the focus is called the perigee, while the point of the orbit farthest away from the focus is called the apogee. 
When the eccentricity ε is equal to 1 or constant A is equal to g(re)2/(rovo)2, the trajectory of the object is an parabolic trajectory, on which the object move around the focus with an infinite radial radius at θ=180o. Since the object does not return to its starting point and the initial velocity is the minimum value such that the object is not following an orbit all the way around the focus, the initial velocity at the specified initial radial radius is called the escape velocity, . 
When the eccentricity ε is greater than 1 or constant A is greater than g(re)2/(rovo)2, the trajectory of the object is an hyperbolic trajectory, on which the object move around the focus with an infinite radial radius at an angle θ less than 180o. Since the initial velocity is greater than the escape velocity, the object does not return to its starting point also. 
When the eccentricity ε is smaller than 0 or constant A is smaller than 0, the trajectory of the object is an elliptic orbit, on which the object move around the focus on the left hand side with an finite radial radius. The minus side before the eccentricity ε or the eccentricity ε is smaller than 0 means that the focus is locate on the left hand side instead of the right hand side and the initial velocity is smaller than the initial velocity for the circular orbit. Similarly the point of the orbit closest to the focus is called the perigee, while the point of the orbit farthest away from the focus is called the apogee. 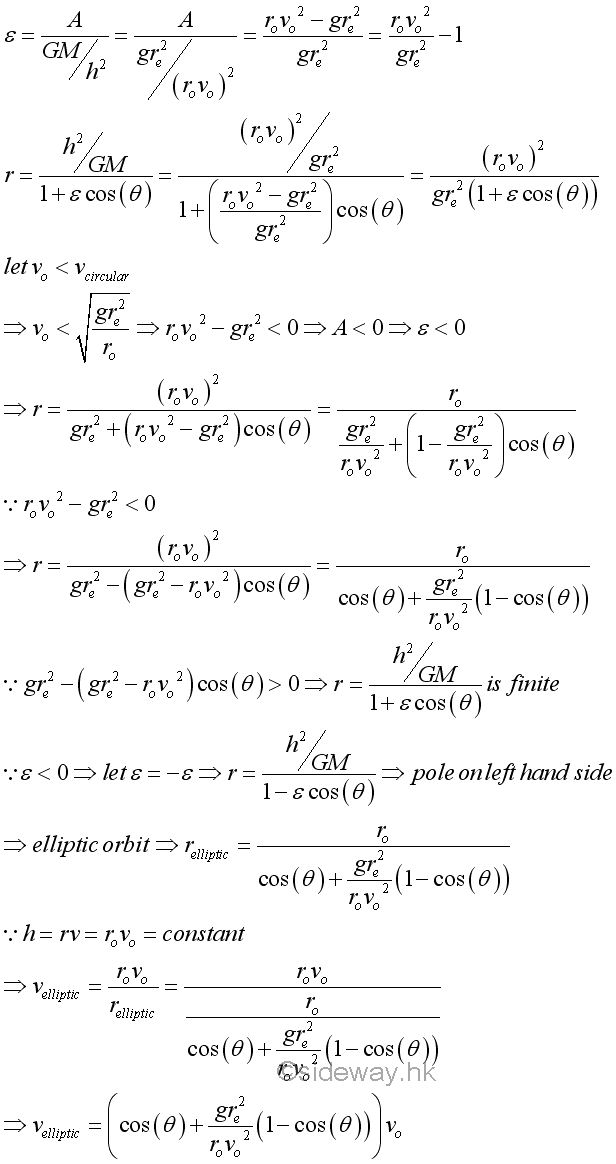
Since the ellipse orbit is starting with the point of the orbit farthest away from the focus, the closest point on the opposite site of the ellipse orbit may intersect with the object located on the focus when the initial velocity is lowered to a critical value. And therefore for any object under a central force with an initial velocity smaller than the initial velocity for a circular orbit, the object always travels along an elliptic trajectory. However when trvalling distance is small such that the gravitational foce acting on the object can be assumed as an uniform parallel force, then the elliptic path can be approximated by a parabolic path as used in many conventional projectile applications. 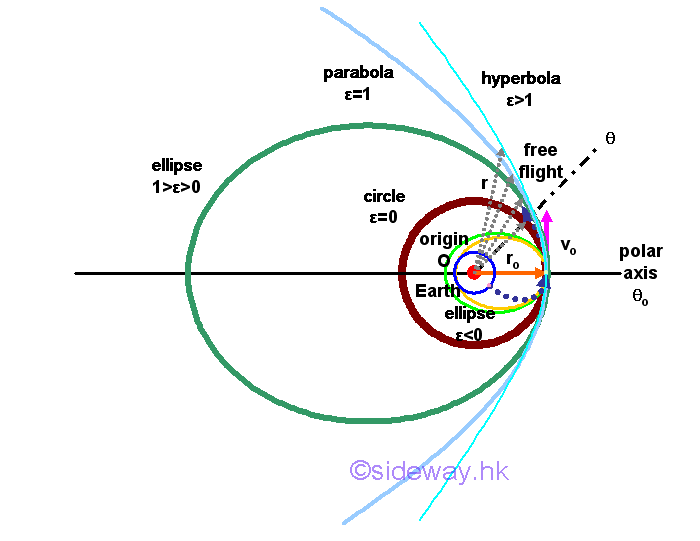
Periodic Time of the Orbit of an Object Under a Central Force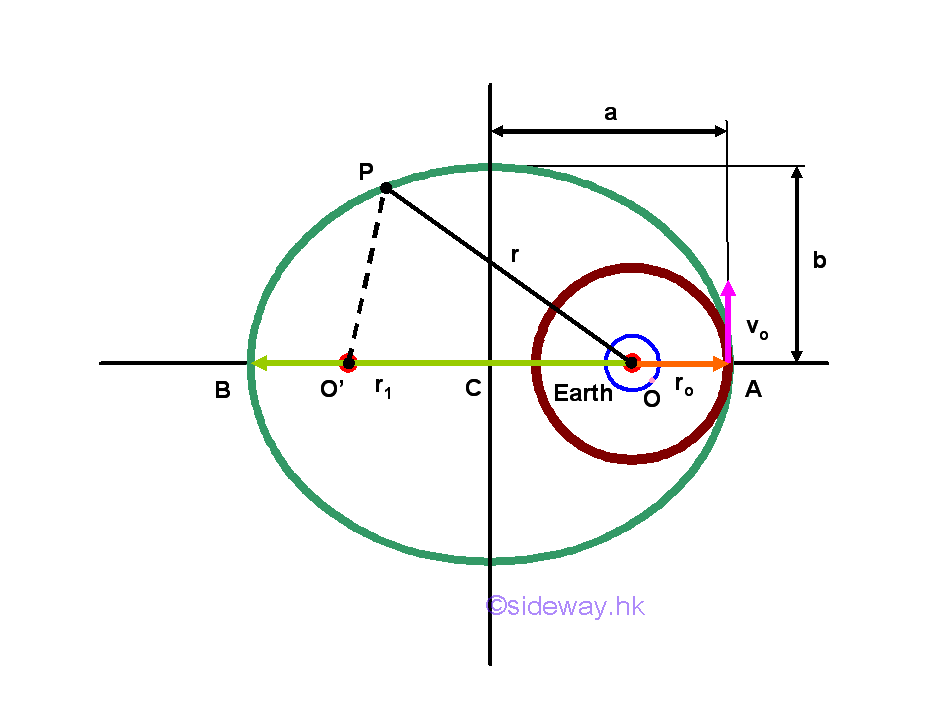
The periodic time of an circular orbit is equal to the circumference of the circular orbit over the constant initial velocity. But for an elliptic orbit, the periodic time of the elliptic orbit can not be obtained from the perimeter of an ellipse easily. Since the exact formula for the circumference of an ellipse is not simple and the velocity of the object is not a constant along the path. However, the area of an ellipse is very easy to calucate and the areal velocity of the object sweeps around the elliptical path is constant. In other words, the total time needed to sweep around the area of the ellipse bounded by the ellipic orbit is equal to the area of the ellipse divided by the areal velocity. 
Kepler's Laws of Planetary MotionThe motion of fast moving projectiles under a central force can also be used to describe the motion of the moon moving around the Earth. The interaction between two objects have the same effect acting upon one another. Since the mass of a projectile is usually small compared with the mass of the Earth, the reaction of the Earth due to the mass of a projectile can be neglected. However, the mass of the Moon comparing with the mass of the Earth is not negligible, and therefore the obtained results will contain error. Similarly, the motion of fast moving projectiles under a central force can also be used to approximate the planetary motion around the sun by neglecting the interaction forces exerted by the planets on one another. A German astronomer Johann Kepler (1571-1630) in the early 1600s proposed three laws of planetary motion before the theory of planetary motion fromulated by Newton. The Kelper's laws of planetary motion are
However, the law of harmonies is only a good approximation for the solar system. And a more general form of the law of harmonies was derived by Isaac Newton making use of the Law of Gravitation for objects under a central force. 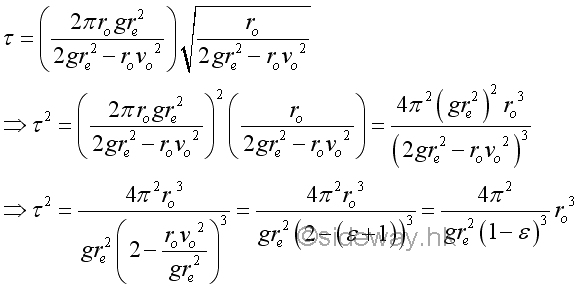
|
Sideway BICK Blog 10/10 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

