Sideway BICK Blog on 10/04 from sideway.to

Sideway BICK BLOG from Sideway

A Sideway to Sideway Home

Home

Output.to

Link:http://output.to/sideway/default.asp?qno=140400004

Elementary Functions

MatLab: Elementary Mathematical Functions

Major Reference Source: MatLab Verson 7.0

Like common scientific calculators, MatLab package also provides some elementary mathematical functions.

Elementary Mathematical Functions

Besides, the baisc arithmetic function for arithmetic operation, there are some other common mathematical functions for scientific calculaton.

Trigonometric Functions
Exponential Functions.
Complex Functions
Rounding and Remainder Functions.
Discrete Mathematics Functions
Mathematical Constant Functions

Trigonometric Functions

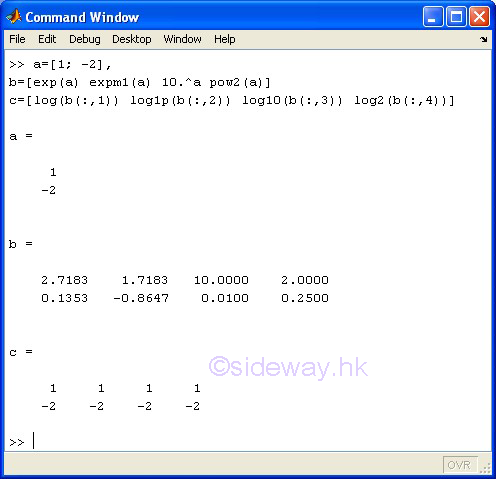
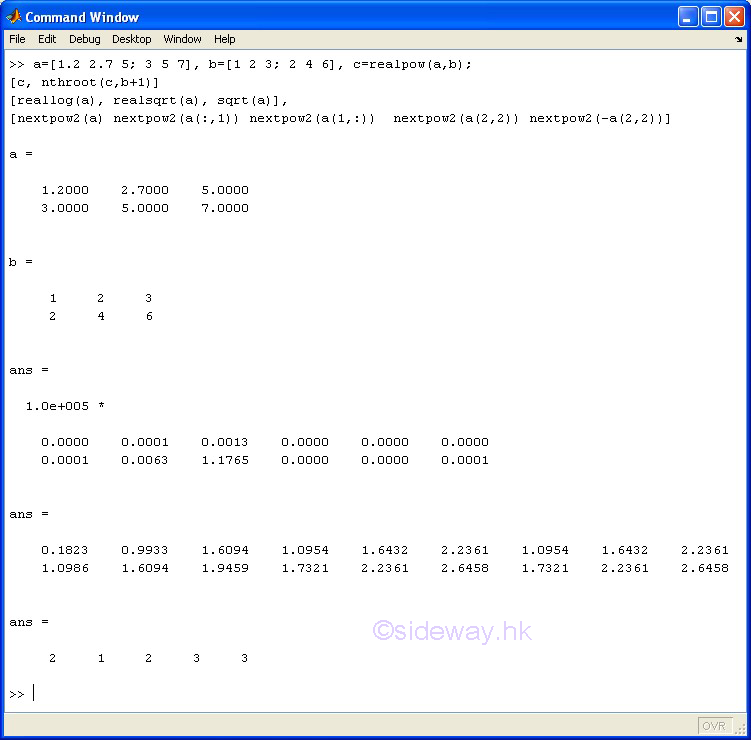
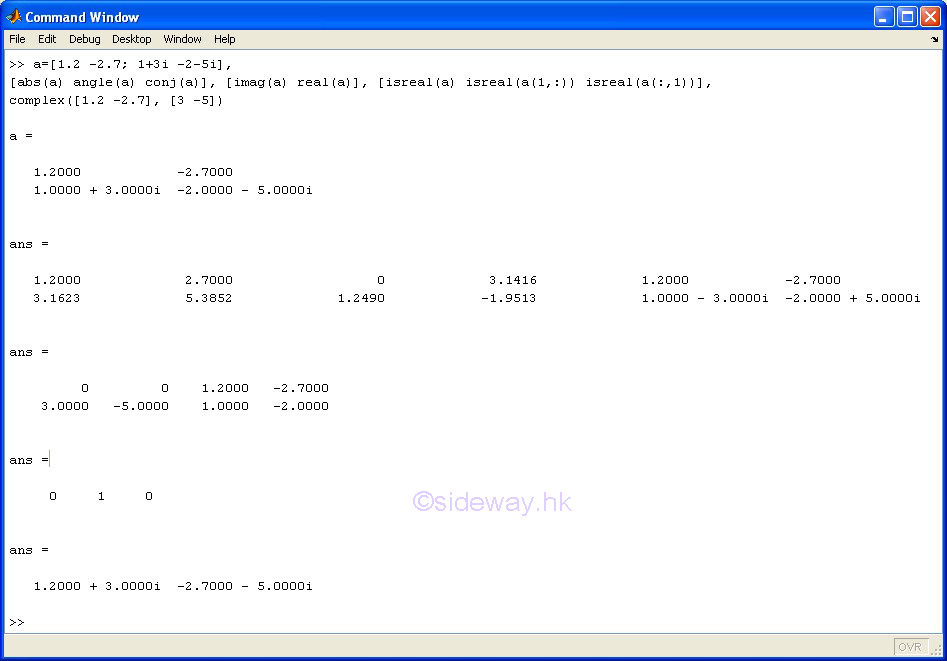
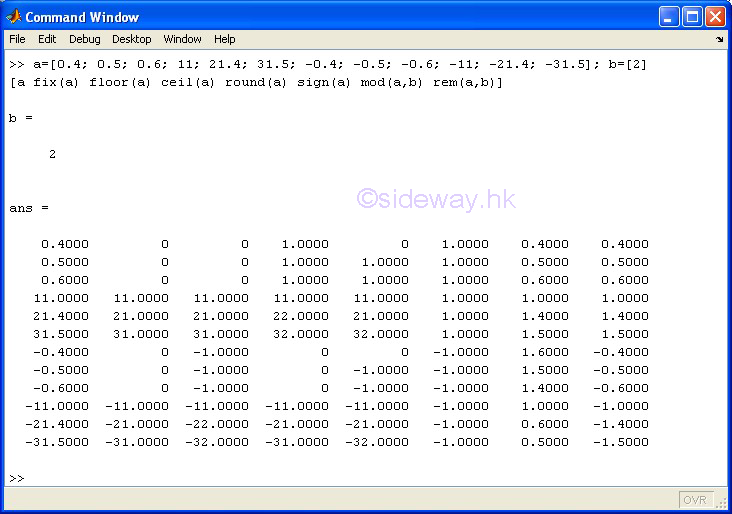
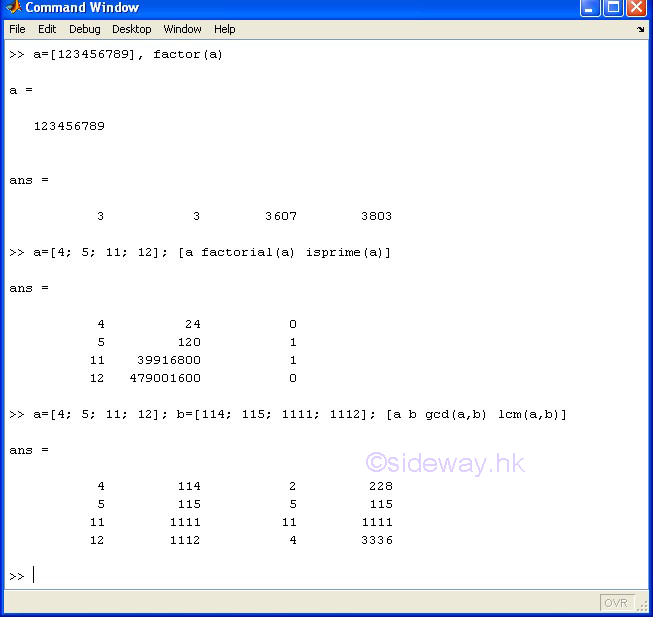
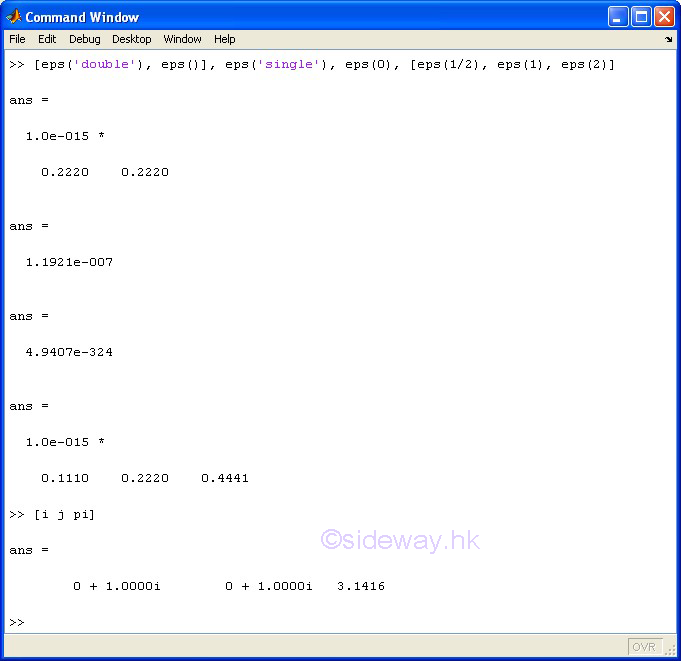
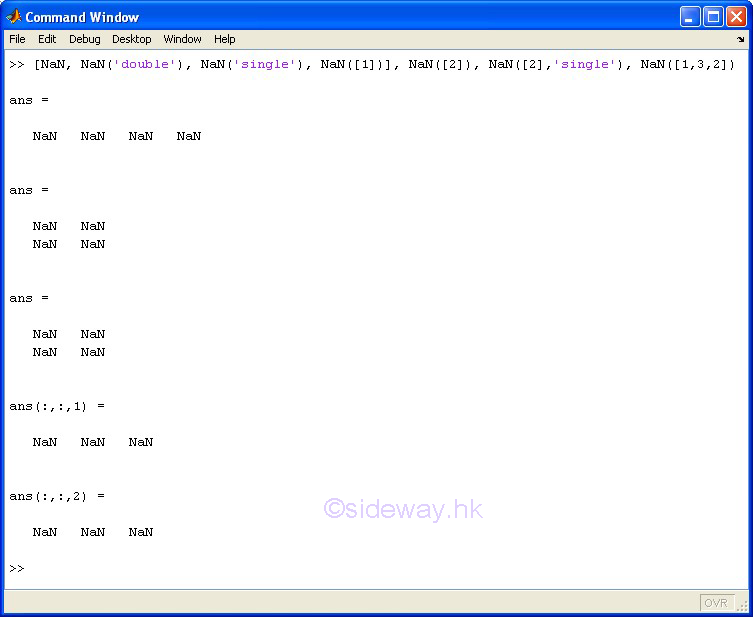
Function	Description
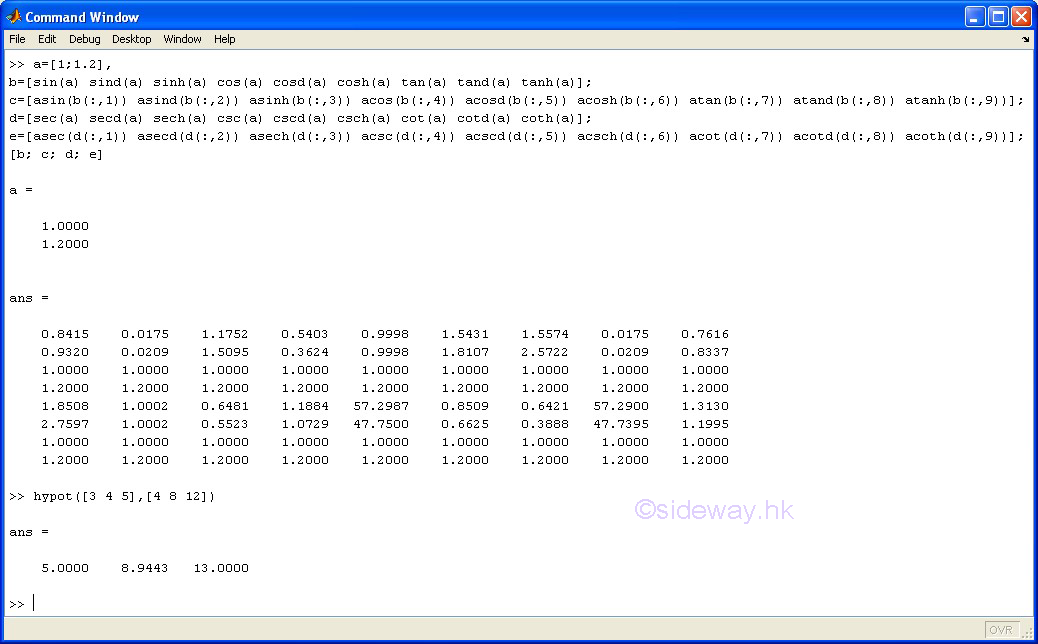
sin(A)	to return the sine of elements of A, in radians.
sind(A)	to return the sine of elements of A, in degrees.
sinh(A)	to return the hyperbolic sine of elements of A.
asin(A)	to return the inverse sine of elements of A. Results in radians.
asind(A)	to return the inverse sine of elements of A, Results in degrees.
asinh(A)	to return the inverse hyperbolic sine of elements of A.
cos(A)	to return the cosine of elements of A, in radians.
cosd(A)	to return the cosine of elements of A, in degrees.
cosh(A)	to return the hyperbolic cosine of elements of A.
acos(A)	to return the inverse cosine of elements of A. Results in radians.
acosd(A)	to return the inverse cosine of elements of A, Results in degrees.
acosh(A)	to return the inverse hyperbolic cosine of elements of A.
tan(A)	to return the tangent of elements of A, in radians.
tand(A)	to return the tangent of elements of A, in degrees.
tanh(A)	to return the hyperbolic tangent of elements of A.
atan(A)	to return the inverse tangent of elements of A. Results in radians.
atand(A)	to return the inverse tangent of elements of A, Results in degrees.
atanh(A)	to return the inverse hyperbolic tangent of elements of A.
sec(A)	to return the secant of elements of A, in radians.
secd(A)	to return the secant of elements of A, in degrees.
sech(A)	to return the hyperbolic secant of elements of A.
asec(A)	to return the inverse secant of elements of A. Results in radians.
asecd(A)	to return the inverse secant of elements of A, Results in degrees.
asech(A)	to return the inverse hyperbolic secant of elements of A.
csc(A)	to return the cosecant of elements of A, in radians.
cscd(A)	to return the cosecant of elements of A, in degrees.
csch(A)	to return the hyperbolic cosecant of elements of A.
acsc(A)	to return the inverse cosecant of elements of A. Results in radians.
acscd(A)	to return the inverse cosecant of elements of A, Results in degrees.
acsch(A)	to return the inverse hyperbolic cosecant of elements of A.
cot(A)	to return the cotangent of elements of A, in radians.
cotd(A)	to return the cotangent of elements of A, in degrees.
coth(A)	to return the hyperbolic cotangent of elements of A.
acot(A)	to return the inverse cotangent of elements of A. Results in radians.
acotd(A)	to return the inverse cotangent of elements of A, Results in degrees.
acoth(A)	to return the inverse hyperbolic cotangent of elements of A.
hypot(A, B)	to return the square root of the sum of squares of elements of A and corresponding elements of B

Examples

Exponential Functions

Function	Description
exp(A)	to return the exponential of elements of A, i.e. the exponential to the power of A
expm1(A)	to return the exp(A)-1 accurately
log(A)	to return the natural logarithm of elements of A
log1p(A)	to return the log(1+x) accurately
log10(A)	to return the common or base 10 logarithm of elements of A
log2(A)	to return the base 2 logarithm of elements of A and dissect floating point number.
pow2(A)	to return the base 2 to the power of elements of A and scale floating point number
realpow(A,B)	to return the base elements of A to the power of the corresponding elements of B. Results must be real.
reallog(A)	to return the natural logarithm of elements of A which must be nonnegative real numbers.
realsqrt(A)	to return the square root of elements of A. Results must be real.
sqrt(A)	to return the square root of elements of A
nthroot(A,B)	to return the Bth root of elements of A. Both A and B must be real
nextpow2(A)	to return the next higher power of 2 such that 2 to the power of return value is greater than or equal to the absolute value of the number A, or the length of the array A.

Examples

Complex Functions

Function	Description
abs(A)	to return the absolute value of elements of A. Or the complex modulus or magnitude of the complex elements of A
angle(A)	to return the phase angle in radians of the complex elements of A
complex(A,B)	to return the complex result from A as real part and B as imaginary part.
conj(A)	to return the complex conjugate of A
imag(A)	to return the complex imaginary part of A
real(A)	to return the complex real part of A
unwrap(A)	to return a smooth A after correcting or unwrapping radian phase angles of A
isreal(A)	to return a true flag, 1, if A is a real array.
cplxpair(A)	to return and sort complex numbers into complex conjugate pairs

Examples

Rounding and Remainder Functions

Function	Description
fix(A)	to return and round A toward zero
floor(A)	to return and round A towards minus infinity
ceil(A)	to return and round A towards plus infinity
round(A)	to return and round A towards nearest integer
mod(A,B)	to return the modulus after division of A by B.
rem(A,B)	to return the remainder after division of A by B
sign(A)	to return the signs of the corresponding element of A

Examples

Discrete Mathematics Functions

Function	Description
factor(A)	to return the vector of prime factors of scalar A.
factorial(A)	to return the factorial of elements of A
gcd(A,B)	to return the greatest common divisor of corresponding elements of A and B.
isprime(A)	to return a flag array for elements of A where a true flag, 1, indicates the corresponding element is a prime.
lcm(A,B)	to return the least common multiple of corresponding elements of A and B.
nchoosek(A,B)	to return the number of combinations of A things taken B at a time for both A and B are non-negative integers or an array of all possible combinations of elements in vector A for taken B a time.
perms(A)	to return an array of all possible permutations of elements in vector A.
primes(A)	to return a vector for the list of prime numbers less than or equal to scalar A.
rat(A,B)	to return the rational fraction approximations of elements of A in terms of the continued fraction according to the specified tolerance B if no output argument is specified.
rats(A,B)	to return the rational fraction approximations of elements of A in terms of rational fraction according to the specified length B.

Examples

Mathematical Constant Functions

Function	Description
eps(A)	to return the positive distance from abs(A) to the magnitude of next larger floating point number of the same precision as A if A is numberic. A can also be a class name of precision. If A is not specified then the default value of A is 1.0 and the default precision of A is 'double'.
i()	to return the system imaginary unit
inf(A)	to return an array of infinity with sizes of each dimension specified in vector A
intmax(A)	to return the largest positive value in the integer class of class name A where the default class name is 'int32' or ''
intmin(A)	to return the smallest negative value in the integer class of class name A where the default class name is 'int32' or ''
j()	to return the system imaginary unit
NaN(A,B)	to return an array of NaN, Not-a-Number, with sizes of each dimension specified in vector A and class of array specifed by optional B where B must be 'single' or the default 'double'.
pi()	to return the floating-point number nearest to the value pi, the ratio of the circumference of a circle to its diameter.
realmax(A)	to return the system largest positive floating-point number of class name A where the default class name is 'double' or ''
realmin(A)	to return the system smallest positive floating-point number of class name A where the default class name is 'double' or ''

Examples

APR 2014

S	M	T	W	T	F	S

		1	2	3	4	5
6	7	8	9	10	11	12
13	14	15	16	17	18	19
20	21	22	23	24	25	26
27	28	29	30

FEB 2011

S	M	T	W	T	F	S

		1	2	3	4	5
6	7	8	9	10	11	12
13	14	15	16	17	18	19
20	21	22	23	24	25	26
27	28

Sideway BICK Blog

10/04