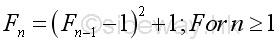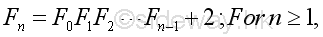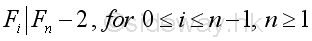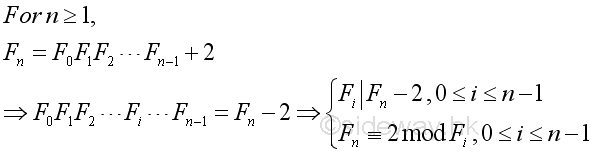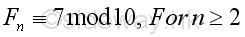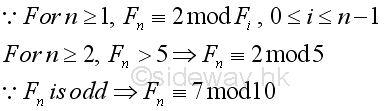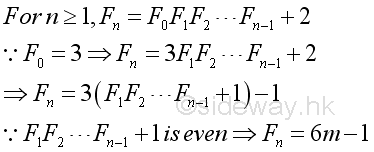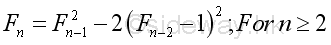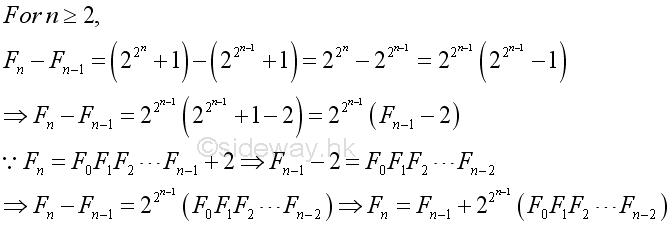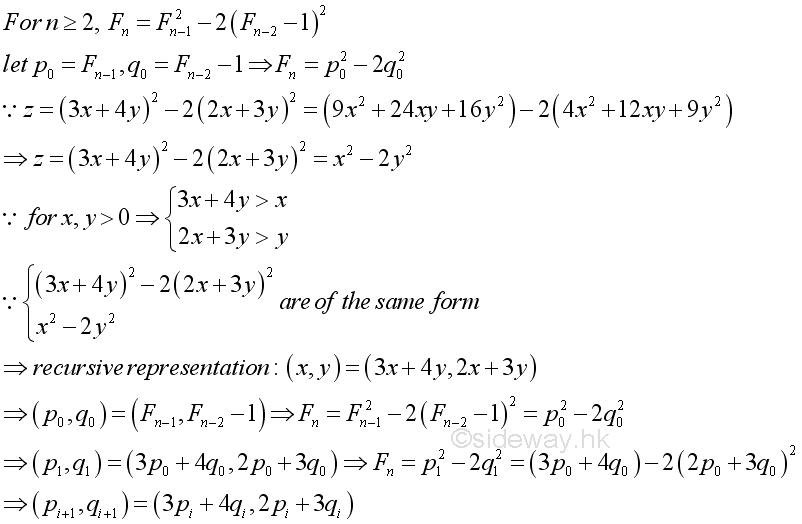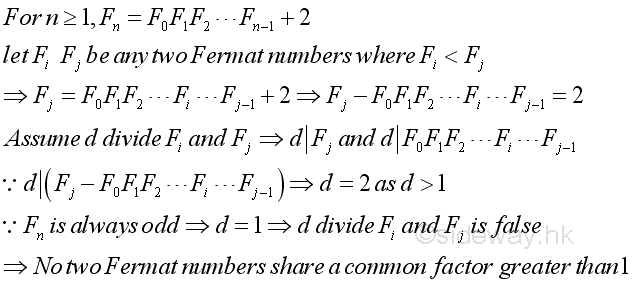Fermat Numbers

For a positive integer of the form 2p+1, the number can be a prime number, only if p is a power of 2. For a number of p with an odd factor, the number must be a composite number. Proof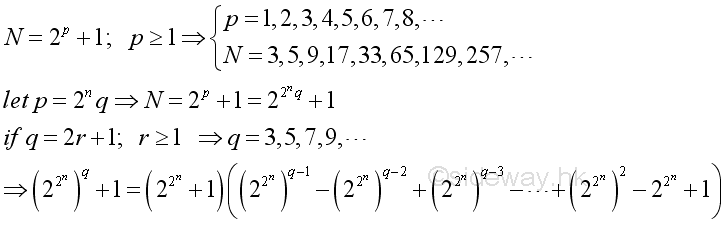

Fermat studied these numbers and found that the first few numbers are prime numbers. Sometimes, but less common, a number of form ap=2p+1 is called Fermat number. But a Fermat number is usually refered to a number with the special case of the form Fn= 22n+1. Primes with this form are therefore called Fermat primes. For examples,

However, Fermat numbers with n greater or equal to 5 are not always prime numbers. In fact, all known Fn as of 2015 are not prime numbers. For example, F5 is a composite.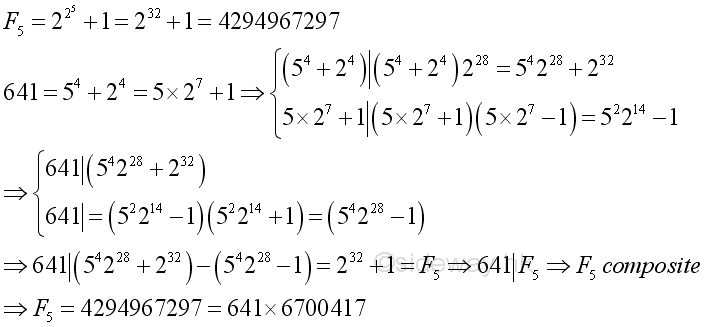

Basic Properties of Fermat Numbers

Basic properties or recurrence relations of Fermat Numbers

Proposition 1

Proof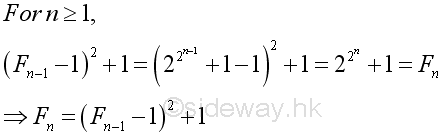

Proposition 2

Proof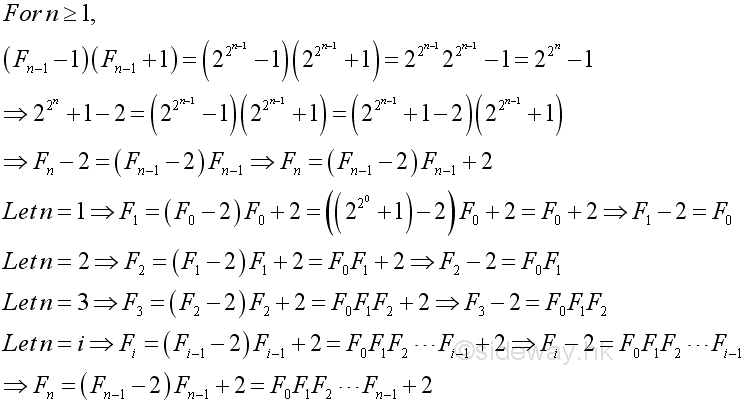

• Corollary 2.1 

  Proof: Proposition 2 also implies that a Fermat number minus 2 is always divisible by all the smaller Fermat numbers for n greater than or equal to 1. Imply

  

• Corollary 2.2 

  Proof: For n greater than or equal to 2, Fn is greater than 5 and the last digit of Fn is always 7. Imply

  

• Corollary 2.3 No Fermat number is a perfect square.

  Proof: For n=0, F0=3. For n=1, F1=5.  For n greater or equal 2, the last digit of Fn is always 7. Since a perfect square can only be congruent to 0, 1, 4, 5, 6, or 9 mod 10. Besides from Proposition 1, for n greater or equal 1, Fn is always equal to a perfect square number plus one, or Fn is always not equal to a perfect square. 

• Corollary 2.4 For n greater than or equal to 1, Fermat number is of the form 6m-1.

  Proof

  

Proposition 3 

Proof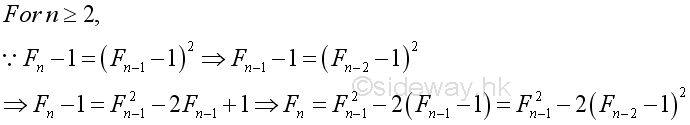

Proposition 4 

Proof

Proposition 5   For n greater than or equal to 2, a Fermat number can has infinitely many representations of the form p2-2q2 where p and q are both positive integers.

Proof: Fermat numbers defined in Proposition 3 are of this form. In other words, for n great than or equal to 2, there always exists a pair of integers p and q. And other pairs of integer can be obtained recursively. Imply

Proposition 6   Any two Fermat numbers Fn=2 2n+1 are pairwise relatively prime to each other.

Proof: From Proposition 2, imply

• Corollary 6.1  There are infinitely many primes.

  Proof: From Proposition  2, imply

  

Proposition 7   For n greater than or equal to 2, no Fermat number can be expressed in terms of the sum of two primes.

Proof: As in Proposition 2, imply