Moment of force about axis
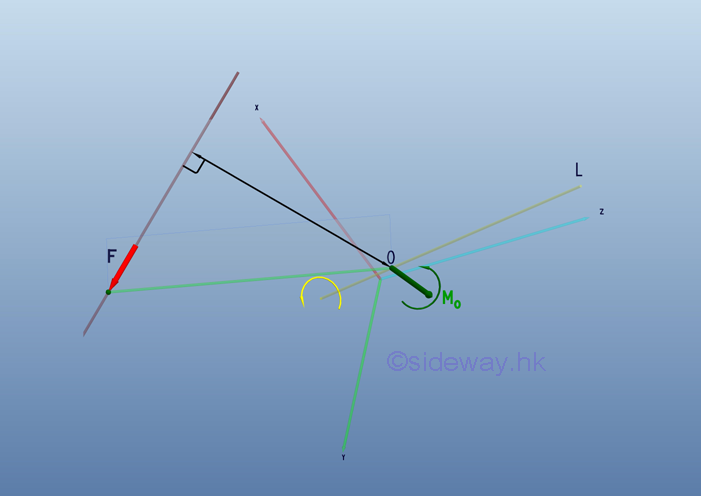
The moment of a force about a reference point is represents by a moment vector, MO normal to the plane formed by the reference point and the line of action of the force. The direction of moment vector also specifies the axis of rotation. Therefore when the rotating axis, OL is specified, the moment of a force is also limited to rotate about the specified rotating axis only.
Force Decomposition
Physically, the effective moment MOL about a specified axis is only due to the force lying on the plane normal to the specied axis and the moment due to the force parallel to the specified axis is zero. Besides, the effective moment MOL and the moment MO also form a rotating angle in the space.
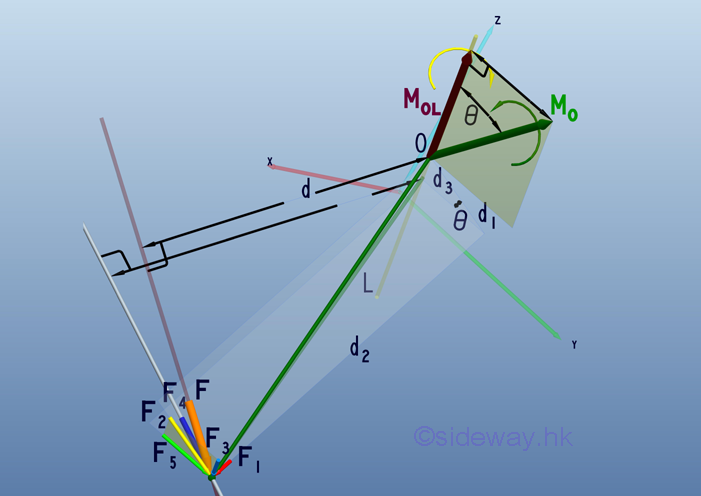
Geometrically, a plane can be constructed by the moment MO of force F about a point O and the axis OL. Therefore force (orange) F can be resolved into force (red) F1 normal to the plane and force (yellow) F2 parallel to the plane. Imply the moment of force F about a point O equals:
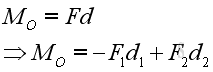
In order to determine the effective moment MOL of the applied force F about the specified axis OL, the applied force F is resolved into two retangular components with one force (cyan) F3 parallel to the specified axis and the other force (blue) F4 lying on the normal plane of the specified axis. Force F4 can further be decomposed into two retangular components with one force equals to the force (red) F1 and the other force (green) F5 lying on the normal plane of the force (red) F1 . Since the force (cyan) F3 is parallel to the specified axis, the moment of the force about the specified axis is equal to zero, Imply the moment of force F about a specificed axis OL equals:
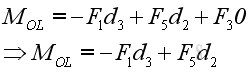
Through force decomposition, force F is resolved into three retangular components, F1, F3, and F5. And Force F2 can also be resolved into two retangular components, F3, and F5. According to the geormetry, force F5 can be expressed as
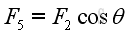
Besides, the moment arm d3, can also be expressed as:
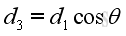
Substitute all variables, and the effective moment MOL equals:
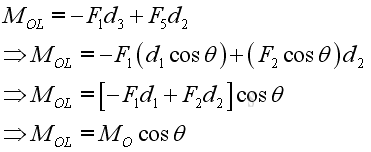
Moment Decomposition
The effective moment about a specified axis can be determined by moment decomposition. The moment, MO can be resolved into two retangular components with the moment, MOL along the specified axis and the other moment normal to the specified axis on a plane formed by the two axes. Therefore the effective moment, MOL about a specified axis is equal to the moment, , MO projected on the axis, OL.
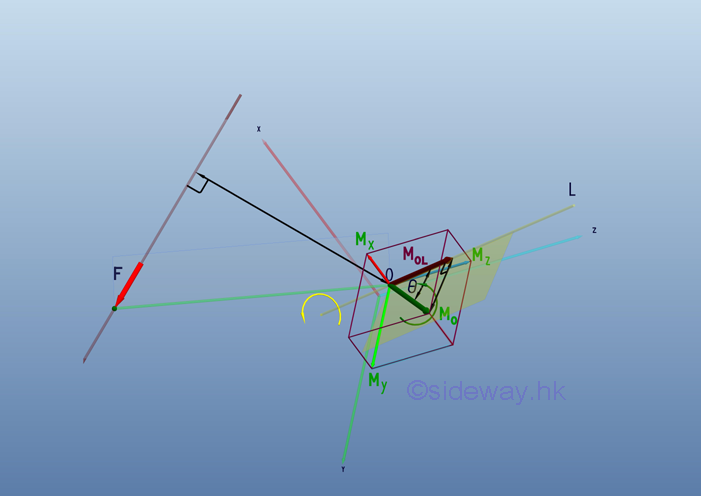
The magnitude of moment vector, MOL can be expressed as:
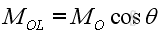
The moment vector, MO in the form of three retangular components is
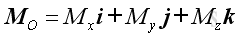
Let the unit vectors of moments, MO and MOL are λO and λOL and they can be expressed as:
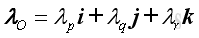 and
and
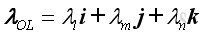
where:
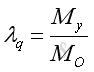 ,
,
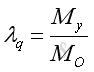 and
and
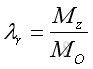
From the law of cosine, imply
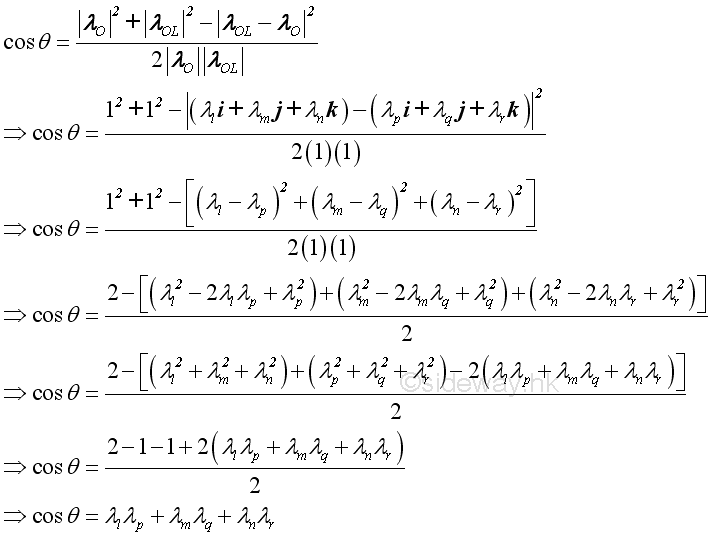
Therefore the moment about the specified axis can be expressed as:
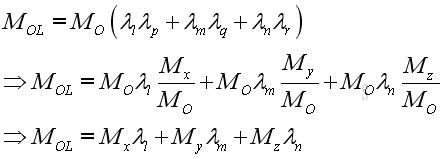
Moment Vector
The magnitude of moment MOL of a force F about a specified axis OL can be defined as the scalar product of the unit vector λOL along the axis OL and MO.
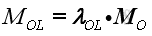
Imply
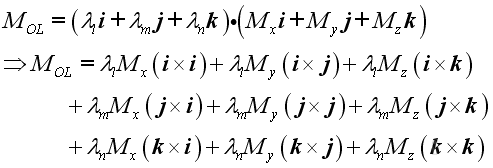
Since the scalar product of two vectors is the product of the magnitudes of the two vectors and the cosine of the angle formed by the vectors, imply
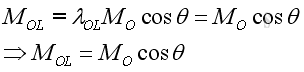
Therefore, the scale product of a unit vector with itselt is equal to one, imply
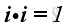 ,
,
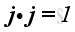 and
and
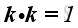
And, the scale product of two different unit vectors is equal to zero, imply
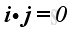 ,
,
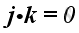 and
and
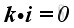
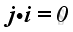 ,
,
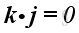 and
and
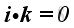
Substitute all variables into the moment vector equation, imply
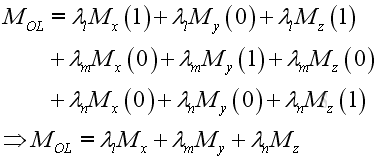 .
.
Since the moment of force about a point can be expressed as the vector product of the position vector and the force vector, imply the magnitude of the moment of force about a fixed axis equals to the mixed triple product of three vectors
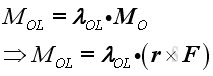 .
.
Imply :
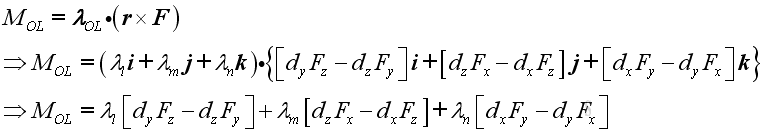 .
.
The magnitude of the moment of force about a fixed axis can also be expressed in the determinant form, :
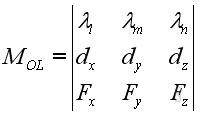 .
.
©sideway
ID: 110600003 Last Updated: 6/19/2011 Revision: 0 Ref:
References
- I.C. Jong; B.G. rogers, 1991, Engineering Mechanics: Statics and Dynamics
- F.P. Beer; E.R. Johnston,Jr.; E.R. Eisenberg, 2004, Vector Mechanics for Engineers: Statics
Latest Updated Links
- Travel Singapore Sight Space(last updated On 12/30/2025)
- Travel Singapore Sight Curiosity Cove(last updated On 12/30/2025)
- Travel Singapore Sight Night Safari(last updated On 12/30/2025)
- Travel Singapore Sight River Wonders(last updated On 12/30/2025)
- Travel Singapore Sight Rainforest Wild ASIA(last updated On 12/30/2025)
- Travel Singapore Sight Singapore Zoo(last updated On 12/30/2025)
- Travel Singapore Sight Mandai(last updated On 12/30/2025)
- Travel Singapore Sight Bird Paradise(last updated On 12/30/2025)
- Travel Singapore Sight AltitudeX(last updated On 12/30/2025)
- Travel Singapore Sight(last updated On 12/6/2025)
- Travel Singapore Rail Network(last updated On 12/5/2025)

 Nu Html Checker
Nu Html Checker  53
53  na
na  na
na
Home 5
Business
Management
HBR 3
Information
Recreation
Hobbies 9
Culture
Chinese 1097
English 339
Travel 31
Reference 79
Hardware 54
Computer
Hardware 259
Software
Application 213
Digitization 37
Latex 52
Manim 205
KB 1
Numeric 19
Programming
Web 289
Unicode 504
HTML 66
CSS 65
SVG 46
ASP.NET 270
OS 431
DeskTop 7
Python 72
Knowledge
Mathematics
Formulas 8
Set 1
Logic 1
Algebra 84
Number Theory 206
Trigonometry 31
Geometry 34
Calculus 67
Engineering
Tables 8
Mechanical
Rigid Bodies
Statics 92
Dynamics 37
Fluid 5
Control
Acoustics 19
Natural Sciences
Matter 1
Electric 27
Biology 1
