 Sideway
BICK BLOG from Sideway
Sideway
BICK BLOG from Sideway
|
Link:http://output.to/sideway/default.asp?qno=150100001 Mechanics Kinetics Energy and Momentum Particle Objects Kinetics: Energy and MomentumWhen the motions of two objects are known, the collision of two objects can be determined by the principle of impulse and momentum together with the concept of impact directly. If one of the objects is expressed in terms of an impulse of a force, the collision can be simplified to the change in momentum of an object over a short time interval. By Newton's second law, F=ma, an impulsive force of any kind can also be considered as the rate of change of the momentum of an object. But for conservative forces, the concept of work and energy can be applied to detemine the motion of an object through the conservation of energy. Conservation of EnergyIn a general sense, energy is the capacity for doing work. From the principle of work and enegy, the change in the kinetic energy of the an object is equal to the work done on the object. For a perfectly elastic impact with no mechanical energy loss, a moving object can be stopped by a collision with an average impact force over a stopping distance traveled through changing the kinetic energy of the object. When the net kinetic motion of an object is due to conservative forces acting upon the object, the net work done on the object is equal to the change in potential energy of the object under the applied force field. Together with the principle of work and energy, the change in kinetic energy of the object must equal to the change in potential energy of the object under a conservative force field. In other words, for the motion of an object caused by a conservative force, the sum of the kinetic energy and potential energy of the object must remain constant, or the total mechanical energy is conserved. Impact and Conservation of Energy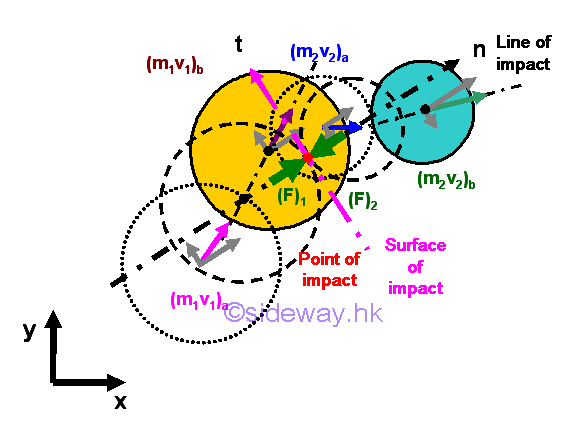
For a perfectly elastic impact, the coefficient of restitution is equal to one and there is no mechanical energy loss during the collision at which both momentum and energy are conserved. For an inelastic impact, the coefficient of restitution is less than one and greater zero, and there is mechanical energy loss during the collision at which only momentum is conserved and both objects move independently at their own velocity. And for a perfectly plastic impact, the coefficient of restitution is equal to zero and there is mechanical energy loss during the collision at which only momentum is conserved and both objects move together at same velocity. When friction between surfaces of impact are neglected, the impulsive forces are always along the line of impact and the equations of an impact are 
Perfectly Elastic ImpactFor a perfectly elastic impact, the coefficient of restitution is equal to one. When friction between surfaces of impact are neglected, the velocities of the two objects before and after impact are 
When friction between surfaces of impact are neglected, the relative velocity along the line of impact after the impact is of the same magnitude but opposite in direction as that of the relative velocity before the impact. 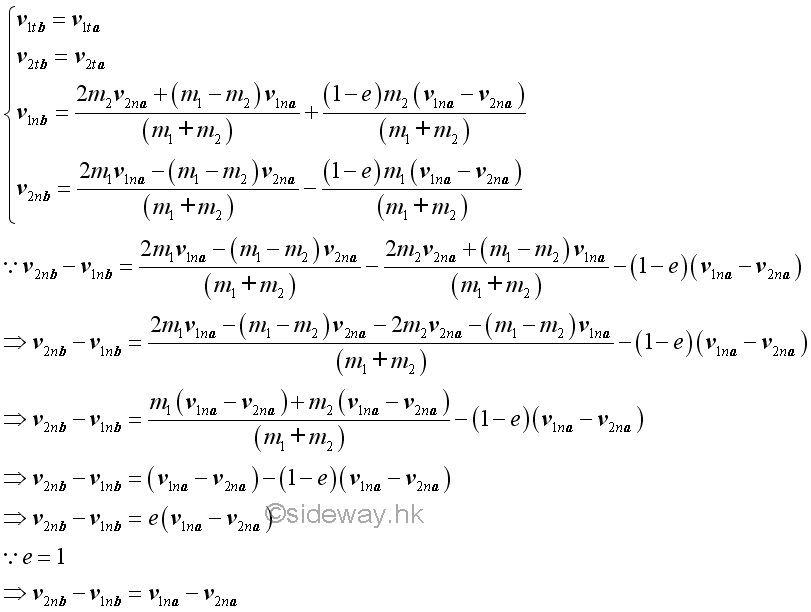
Since there is no external force and friction between surfaces of impact are neglected, the total momentum must be conserved. 
Since there is no energy loss and friction between surfaces of impact are neglected, the total energy must be conserved. 
Impact of Equal Mass ObjectsIf the masses of the two objects are of the same mass m, the general equations of the impact can be simplified. When friction between surfaces of impact are neglected, the velocities of the two objects before and after impact are 
For perfectly elastic impact, the velocities of the two objects along the line of impact are exchanged. For perfectly plastic impact, the velocities of the two objects along the line of impact become the same. When friction between surfaces of impact are neglected, the relative velocity along the line of impact before and after the impact still depends on the coefficient of restitution only, since the velocity after the impact is indepent of the masses of the two objects. 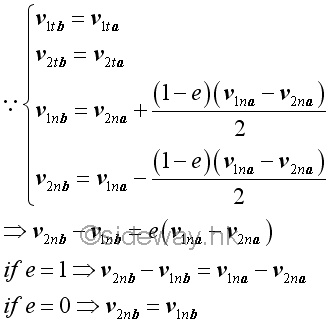
For perfectly elastic impact, the relative velocities of the two objects along the line of impact after the impact is of the same magnitude but opposite in direction as that of the relative velocity before the impact. For perfectly plastic impact, the relative velocity of the two objects along the line of impact is equal to zero, that is the velocities of two objest along the line of impact become the same and the average velocity of the velocities of the two objects along the line of impact. Since there is no external force and friction between surfaces of impact are neglected, the total momentum must always be conserved. 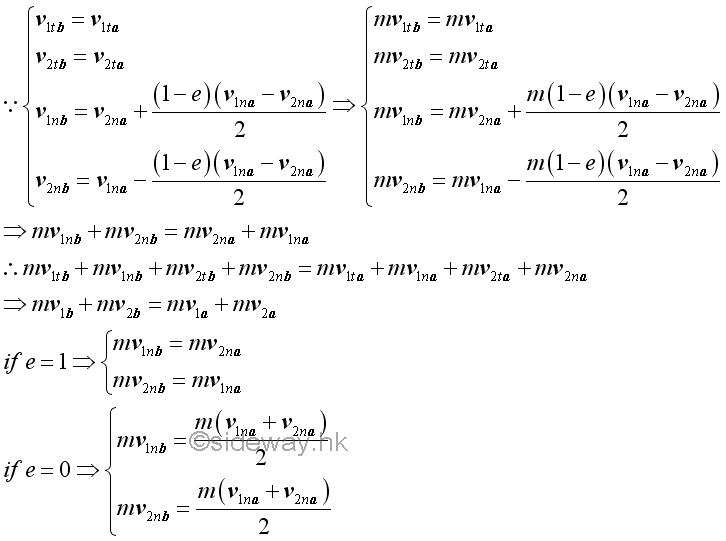
By the principle of impulse and momentum, the total momentum of the two object is conserved whenever there is no external impulsive force acting on the two objects. For perfectly elastic impact, the velocities of the two objects along the line of impact are exchanged, the momentums of the two objects along the line of impact are also exchanged since both objects are of the same mass. For perfectly plastic impact, since the velocities of the two objects along the line of impact become the same, the momentums of the two objects along the line of impact are also the same since both objects are of the same mass. Let friction between surfaces of impact are neglected, the total energy of the two particles are. 
For perfectly elastic impact, the velocities of the two objects along the line of impact are exchanged, the total energy of the two objects are also exchanged since both objects are of the same mass. For perfectly plastic impact, since the velocities of the two objects along the line of impact become the same, the total energy of the two objects along the line of impact are reduced by half of the energy due to the relative velocity of the two objects. Impact of One Object at Rest InitiallyIf the initial velocity of object 2 is at rest, the general equations of the impact can be simplified. When friction between surfaces of impact are neglected, the velocities of the two objects before and after impact are 
For perfectly elastic impact, the velocities of the two objects along the line of impact are changed according to the masses of the two objects. If mass 1 is greater than mass 2, object 1 continues to move in the same direction but the velocity is reduced in magnitude. When two objects are of the same mass, the motion of object 1 is now stopped and object 2 moves with the same initial velocity of object 2. If mass 1 is smaller than mass 2, the object 1 bounces back in the opposite direction of the initial velocity and the magnitude of velocity is reduced. And when mass 1 is much smaller than mass 2, by approximation, the object 1 bounces back in the opposite direction of the initial velocity with the same magnitude as the initial velocity, while object 2 remains stop in motion. For perfectly plastic impact, both objects moves at the same direction as in the initial velocity and the velocities of the two objects along the line of impact become the same. When friction between surfaces of impact are neglected, the relative velocity along the line of impact after the impact is of the same magnitude but opposite in direction as that of the relative velocity before the impact. 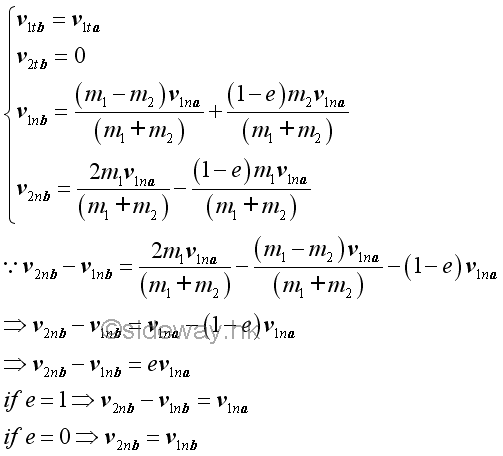
For perfectly elastic impact, the relative velocities of the two objects along the line of impact after the impact is of the same magnitude but opposite in direction as that of the relative velocity before the impact. For perfectly plastic impact, the relative velocity of the two objects along the line of impact is equal to zero, that is the velocities of two objest along the line of impact become the same. Since there is no external force and friction between surfaces of impact are neglected, the total momentum must always be conserved. 
Let friction between surfaces of impact are neglected, the total energy of the two particles are. 
Only for perfectly elastic impact, the total energy of the two objects is conserved. Example of Curling Stones Collision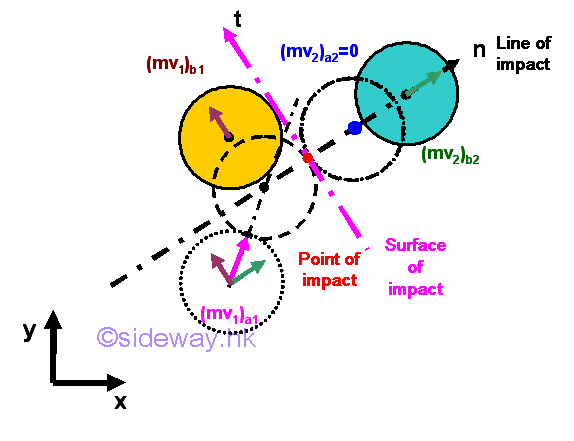
Assuming a curling stone of mass m is at rest initially and another curling stone of mass m moves at initial velocity, v. For perfectly elastic impact and neglecting the friction between the surface of impact, the motion of the two curling stones are 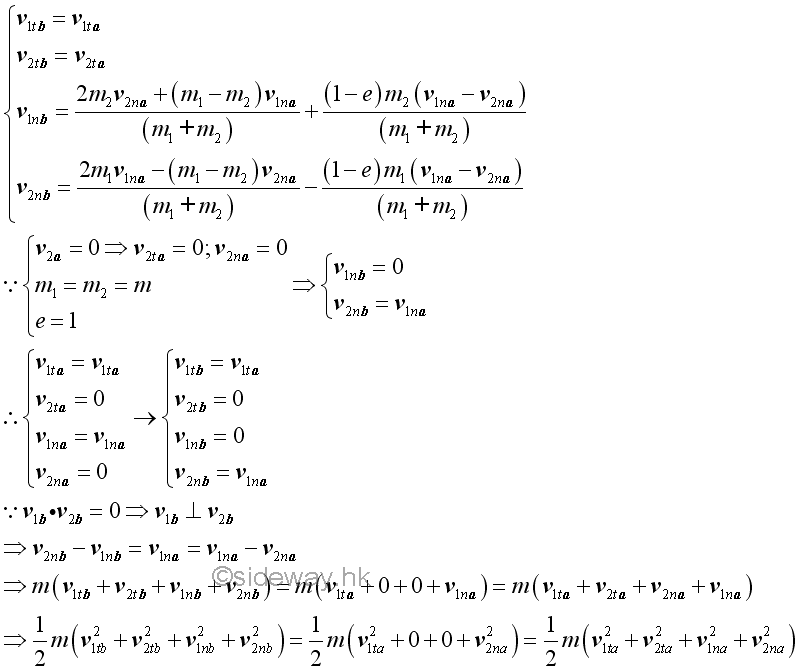
If there is no external force, total momentum of the two curling stones is conserved. For perfectly elastic impact, the total energy of the two curling stones is conserved and the relative velocity of the two curling stones along the line of impact after the impact is of the same magnitude but opposite in direction as that of the relative velocity before the impact. For equal mass, the velocities of the two curling stones along the line of impact are exchanged. Since one of the object at rest initially, the motions of the two curling stones after the impact are always perpendicular to each other. Example of Ballistic Pendulum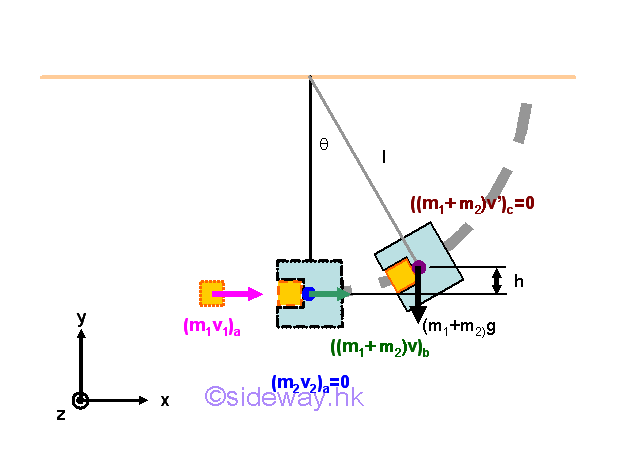
A bullet block of mass m1 collides with a ballistic pendulum block with length l and mass m2 and is lodged in the pendulum block. After the bullet hit, the pendulum block together with the bullet block swings up until makes a maximum angle θ with the vertical. As the ballistic pendulum collision is a perfectly plastic dissipative collision, the total energy of the colliding objects is not conserved. But since there is no external force acting on the two objects along with the motion of the object, the total momentum of the two objects is conserved. After the collision, the motion of pendulum block together with the bullet block are driven by the total remaining energy retained by converting all the kinetic energy into potential energy to swing the combined pendulum upward at the highest point since the gravitation force acting upon the pendulum is conservative. In other words, the total mechanical energy, potential energy and kinetic energy, is conserved. 
Example of Newton's Cradle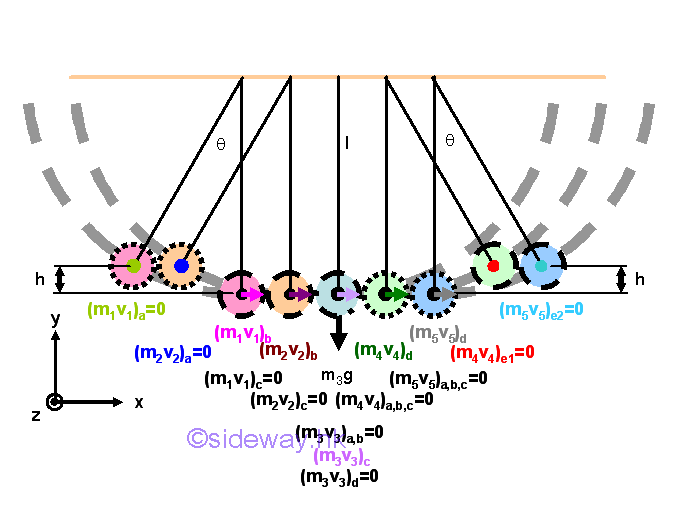
A Newton's cradle is usually a five metal spheres of identical size suspended in a rigid frame such that all spheres touch one another in line at rest. The motion of the Newton's cradle is initiated by swinging one or more spheres of the same level down to collide with the remaining spheres. As each sphere only contacts each other in a line, each sphere can move individually following its only motion. In order to simplify the study, a simple pair-wise collision approach is used without considering the neighborhood sphere and the releasing level of spheres is limited to the same level so that interference between the motion of spheres are eliminated. The collisions of metal spheres along a horizontal line in a Newton's cradle are assumed to be perfectly elastic direct central impacts, the total energy of the Newton's Cradle is conserved. Since there is no external force act upon the line of impact, the total momentum of the Newton's Cradle is also conserved. As all the suspended bobs are of the same mass, the velocities of the colliding bobs is exchanged when two bobs collide to each other. Besides, since the gravitation force acting upon the spheres of Newton's cradle is conservative, the total mechanical energy, potential energy and kinetic energy, is conserved. Therefore, in general sense, both the total energy and the toal momentum of a Newton's crade are convseved. And the kinetic energy of a moving sphere is completely exchanged with the stationary sphere under a perfectly elastic direct central impact of the same mass. 
Example of Falling Object on Spring Scale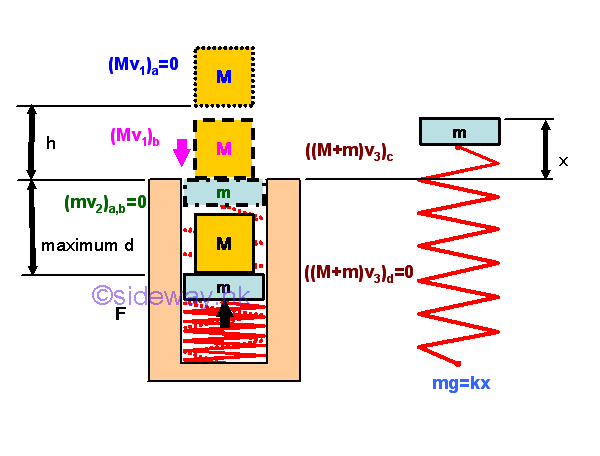
A mass M dropping from h about the pan of a spring scale produces an impact onto the spring scale. The generated impulsive force causes an additional deflection of the spring before the reading of the spring scale rebounds to actual reading. The velocity of mass M at the instant of impact can be determined kinematically or by the principle of conservation of energy. Assuming the impact is perfectly plastic, although the total energy of the impact is not conversed, the total momentum of the combined mass and pan can be assumed to be conversed during the impact by neglecting the weight of mass and the weight of pan is balanced by the spring force. The deflection of spring can then be determined by applying the principle of conservation of energy to the combined mass and pan. Since the combined mass and pan is under two kinds of conservative forces, that is the gravitational force and the elastic spring force, two types of pontential energy should be considered. Let the level just after the instant of impact be the ground level of the potential energy of gravitational force. Then the total energy of the combined mass and pan at the ground level is equal to the sum of kinetic energy created by the impact at the point of impact and the potential energy of the spring acting upon the combined mass and pan with respect to the undeformed position of the spring. The spring of the spring scale is compressed to a maximum deflection position until all kinetic energy is transformed into potential energy. At the level of maximum deflection, all the kinetic energy is transformed into the potential energy. The gravitational potential energy of the combined mass and pan is reduced because the level is lowed below the ground level. The elastic potential energy due to the spring force is changed according to the position of the combined mass and pan with respect to the undeformed position of the spring. 
|
Sideway BICK Blog 01/01 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

